آموزش ریاضی پایه دوازدهم تجربی
دوره تناوب ریاضی دوازدهم تجربی 🚰📝 – به آسانی آب خوردن!
در این درسنامه به مبحث دوره تناوب ریاضی دوازدهم تجربی میپردازیم. ابتدا تابع متناوب و دوره تناوب را معرفی میکنیم. سپس، مثالهایی را از نحوۀ به دست آوردن دوره تناوب ریاضی دوازدهم تجربی و همچنین تعیین ضابطۀ تابع به وسیلۀ آن حل خواهیم کرد.
دوره تناوب و تابع متناوب
به نمودار تابع \(\Large y=\sin x\) که در شکل زیر رسم شده است نگاه کنید:
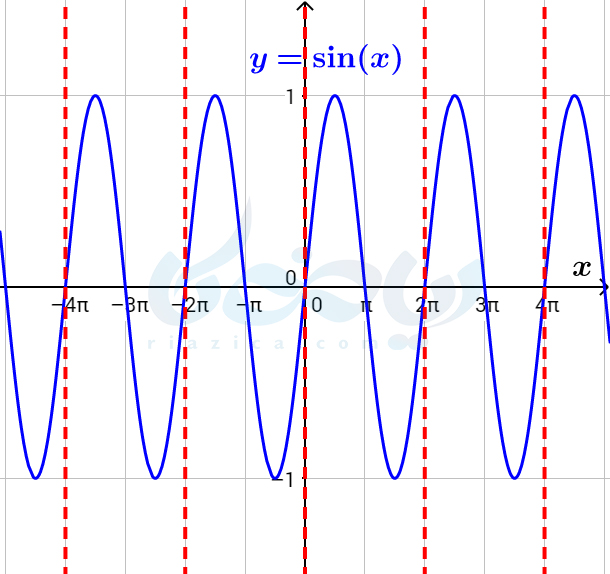
همان طور که میبینید اگر نموار تابع در طول بازهای به اندازۀ \(\Large 2 \pi\) را تکرار کنیم، نمودار تابع در کل محور \(\Large x\)ها به دست میآید. بازههایی به طول \(\Large 4\pi\)، \(\Large 6\pi\) و … نیز چنین خاصیتی دارند. تناوب یعنی همین، یعنی تکرار! اگر به منحنی بین خطچینهای قرمز رنگ نگاه کنید، میبینید که نمودار بین هر دو خطچین قرمز رنگ، دائماً تکرار میشود. به چنین توابعی توابع متناوب گفته و کوچکترین بازهای که تابع دارای این خاصیت باشد، دوره تناوب میگوییم. به طور دقیق تر تعریف تابع متناوب و دوره تناوب به صورت زیر است:
تعریف: تابع \(\Large f\) با دامنۀ \(\Large D_f\) را در نظر بگیرید. اگر عدد حقیقی مثبتی مانند \(\Large T\) وجود داشته باشد که به ازای هر \(\Large x \in D_f\) داشته باشیم \(\Large x \pm T \in D_f\) و \(\Large f(x \pm T)=f(x)\)، تابع \(\Large f\) را تابع متناوب میگوییم. به کوچکترین عدد مثبت \(\Large T\) که چنین خاصیتی داشته باشد، دوره تناوب تابع \(\Large f\) میگوییم.
مثال 1: دوره تناوب توابع \(\Large f(x)=\sin x\) و \(\Large g(x)=\cos x\) را به دست آورید.
حل: اگر نمودار تابع \(\Large f(x)=\sin x\) یا \(\Large g(x)=\cos x\) را در بازهای به طول \(\Large 2 \pi\) تکرار کنیم، نمودار تابع در کل محور \(\Large x\)ها به دست میآید. به عبارتی دیگر داریم:
\(\LARGE \sin (x \pm 2\pi)=sin(x)\)
\(\LARGE \cos (x \pm 2\pi)=cos(x)\)
برای اینکه بهتر متوجه شوید، میتوانید دایرۀ مثلثاتی را که در شکل زیر رسم شده است، در نظر بگیرید.
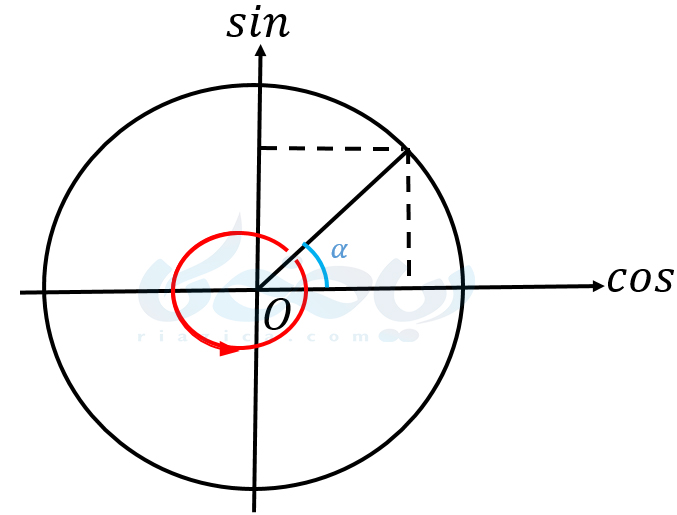
اگر از زاویهای مانند \(\Large \alpha\)، مقدار \(\Large 2 \pi\) رادیان در جهت عقربههای ساعت یا در خلاف جهت عقربههای ساعت حرکت کنیم، دوباره روی زاویهی \(\Large \alpha\) قرار میگیریم. بنابراین سینوس و کسینوس زاویۀ جدید برابر با همان سینوس و کسینوس زاویۀ \(\Large \alpha\) خواهد بود.
دوره تناوب تابع \(\Large f(x)=a\sin x +c\)
میخواهیم دوره تناوب توابعی به شکل \(\Large a\sin x+c\) را به دست آوریم. همانگونه که میدانید، میتوانیم نمودار این توابع را با استفاده از ضرب نمودار \(\Large \sin x\) در \(\Large a\) و انتقال عمودی آن به اندازۀ \(\Large c\) رسم کنیم. برای اینکه بهتر متوجه شوید، نمودار توابع \(\Large y= \sin x\) و \(\Large y=2 \sin x\) و \(\Large y=2 \sin x+3\) در شکلهای زیر رسم شده است.
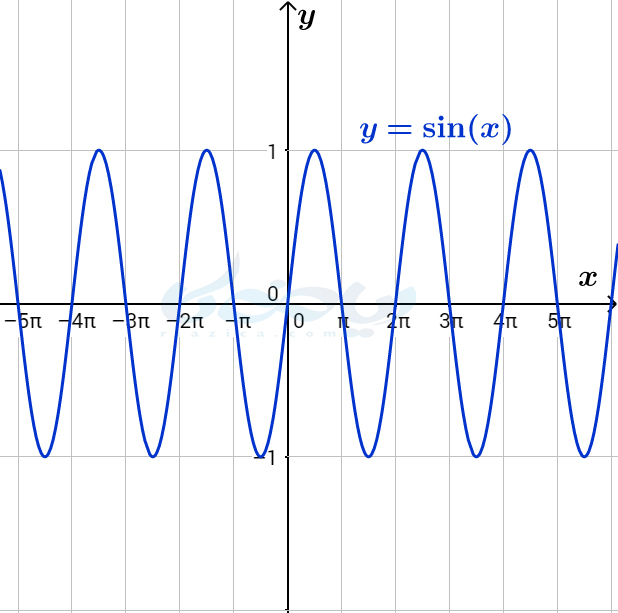
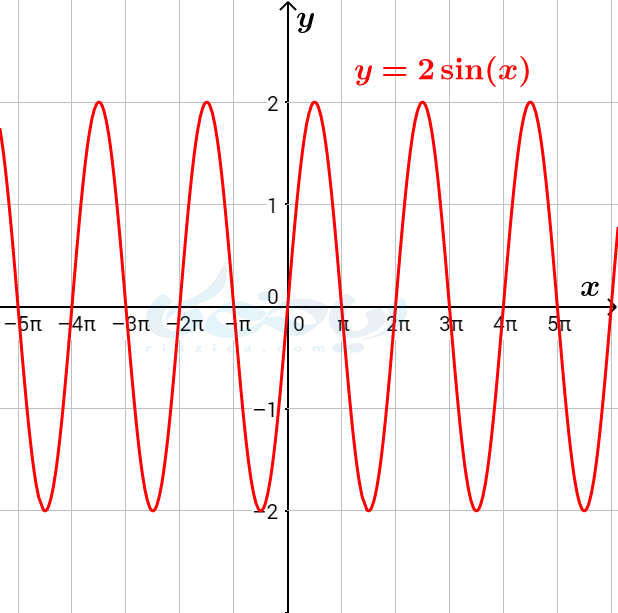
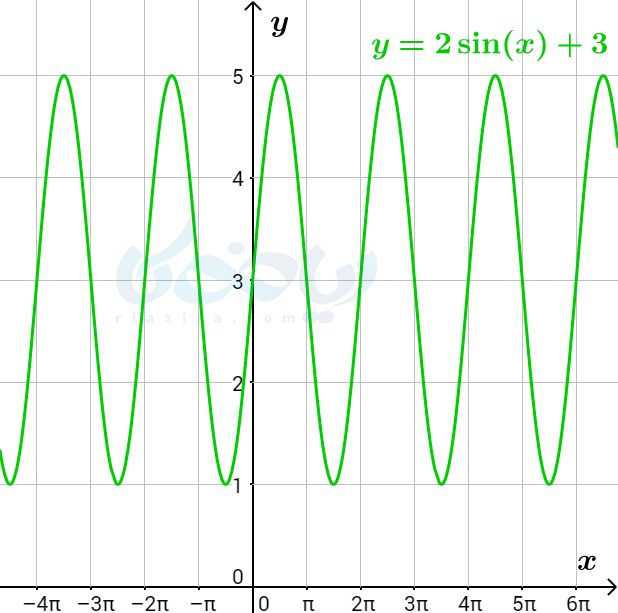
همان طور که در هر سه نمودار میبنید، اگر نمودار تابع در بازهای به اندازۀ \(\Large 2\pi\) را در کل محور \(\Large x\)ها تکرار کنیم، نمودار کل به دست میآید. به عبارت دیگر، ضریب \(\Large a\) که برابر با \(\Large 2\) است و انتقال \(\Large c\) که برابر با \(\Large 3\) است، تغییری در دوره تناوب ایجاد نکرده است. این موضوع را میتوان با استفاده از تعریف دوره تناوب نیز مشاهده کرد:
\(\Large a\sin (x\pm 2\pi)+c=a \sin x+c\)
بنابراین، دوره تناوب تابعی به شکل \(\Large a \sin x+c\) برابر با \(\Large 2 \pi\) است. باید دقت کنیم که اگرچه انتقال عمودی نمودار که به واسطۀ مقدار \(\Large c\) انجام میشود، تاثیری در دوره تناوب تابع ندارد، اما ماکزیمم و مینیمم تابع را تغییر میدهد. از آنجاییکه سینوس یک زاویه بین \(\Large -1\) و \(\Large 1\) است، ماکزیمم تابع \(\Large f(x)=a \sin x+c\) در صورت مثبت بودن \(\Large a\) زمانی اتفاق میافتد که \(\Large \sin x\) برابر با یک شود. درصورت منفی بودن \(\Large a\) نیز ماکزیمم زمانی اتفاق میافتد که \(\Large \sin x\) برابر با منفی یک شود. در این صورت مقدار ماکزیمم برابر خواهد بود با \(\Large |a|+c\). همچنین مینیمم تابع \(\Large f(x)=a \sin x+c\) در صورت مثبت بودن \(\Large a\) زمانی رخ میدهد که \(\Large \sin x\) برابر با منفی یک شود. درصورت منفی بودن \(\Large a\) نیز مینیمم زمانی اتفاق میافتد که \(\Large \sin x\) برابر با مثبت یک شود. در این صورت مقدار مینیمم برابر خواهد بود با \(\Large -|a|+c\).
در مثال بالا مقدار ماکزیمم ۵=۲+۳ ومقدار مینیمم ۱=۳+۲-میباشد که در نمودار نیز مشاهده می کنید.
دوره تناوب تابع \(\Large f(x)=\sin bx +c\)
همان طور که در قسمت قبل دیدیم، انتقال عمودی نمودار تابع، تاثیری در دوره تناوب آن نداشت. لذا برای بررسی دوره تناوب تابع \(\Large\sin bx+c\) کافی است تاثیر ضریب \(\Large b\) را بررسی کنیم. نمودار توابع \(\Large y=\sin x\) و \(\Large y=\sin 2x\) و \(\Large y=\sin(-\frac{x}{3})\) در شکلهای زیر رسم شده است.

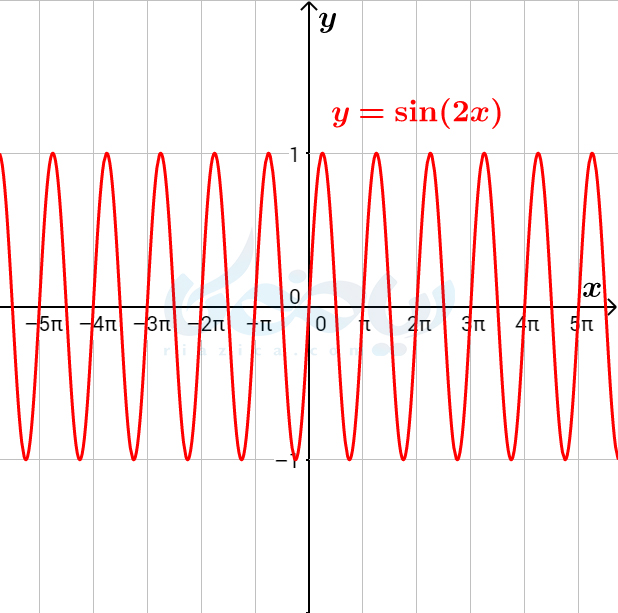
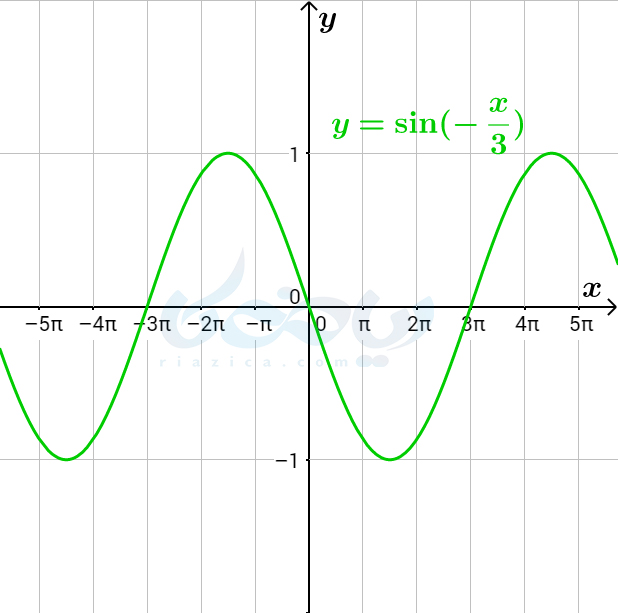
همان طور که میبینید، با توجه به تعریف دوره تناوب، دوره تناوب نمودار اول برابر با \(\Large 2\pi\)، دوره تناوب نمودار دوم برابر با \(\Large \pi\) و دوره تناوب نمودار سوم برابر با \(\Large 6\pi\) است. به بیان دیگر، دوره تناوب تابع \(\Large \sin bx+c\) برابر است با \(\Large 2\pi\) تقسیم بر قدرمطلق ضریب \(\Large b\). این مطلب را با استفاده از تعریف دوره تناوب نیز میتوان به صورت زیر یافت:
\(\LARGE \sin b(x \pm \frac{2\pi}{|b|})\)
\(\LARGE =\sin (bx \pm 2\pi)\)
\(\LARGE =\sin bx\)
بنابراین، همان طور که دیدیم، دوره تناوب تابع \(\Large f(x)=\sin bx+c\) برابر است با \(\Large \frac{2\pi}{|b|}\). باید در نظر داشته باشیم که بر خلاف قسمت قبل، ضریب \(\Large b\) تاثیری در مقدار ماکزیمم یا مینیمم تابع ندارد،ولی باعث انقباض وانبساط نمودار می شود.. در واقع ماکزیمم تابع \(\Large f(x)=\sin bx+c\) زمانی اتفاق میافتد که \(\Large \sin bx\) برابر با \(\Large 1\) باشد. در این صورت مقدار ماکزیمم تابع برابر خواهد بود با \(\Large 1+c\). مینیمم تابع \(\Large f(x)=\sin bx+c\) نیز زمانی اتفاق میافتد که \(\Large \sin bx\) برابر با \(\Large -1\) باشد. در این صورت مقدار مینیمم تابع برابر خواهد بود با \(\Large -1+c\).
دورۀ تناوب توابع سینوسی و کسینوسی
در دو قسمت قبل، دوره تناوب توابع به شکل \(\Large f(x)=a\sin x+c\) و \(\Large f(x)=\sin bx+c\) را بررسی کردیم. همان طور که دیدیم، ضریب \(\Large a\) و انتقال \(\Large c\) تاثیری روی دوره تناوب نداشته، در عین حال مقدار ماکزیمم و مینیمم را تغییر میدهند. اما درست برعکس \(\Large a\) و \(\Large c\)، ضریب \(\Large b\) روی دوره تناوب تاثیر گذاشته ولی مقدار ماکزیمم و مینیمم را تغییر نمیدهد. تمام این موارد برای توابع کسینوسی به شکل \(\Large f(x)=a\cos x+c\) و \(\Large f(x)=\cos bx+c\) نیز برقرار است. بنابراین نکاتی را که گفتیم میتوان در دو بند زیر خلاصه کرد:
- توابعی به شکل \(\Large f(x)=a\sin bx+c\) و \(\Large f(x)=a\cos bx+c\) دارای دوره تناوب \(\Large \frac{2\pi}{|b|}\) هستند.
- توابعی به شکل \(\Large f(x)=a\sin bx+c\) و \(\Large f(x)=a\cos bx+c\) دارای ماکزیمم \(\Large f(x)=|a|+c\) و مینیمم \(\Large f(x)=-|a|+c\) هستند.
مثال از پیدا کردن ماکزیمم و مینیمم و دوره تناوب
مثال 2: مقادیر ماکزیمم و مینیمم و دوره تناوب تابع \(\Large f(x)=\frac{-1}{3}\cos(4\pi x)+2 \) را به دست آورید.
حل:
\(\LARGE max=|\frac{-1}{3}|+2=\frac{7}{3}\)
\(\LARGE min=-|\frac{-1}{3}|+2=\frac{5}{3}\)
\(\LARGE T=\frac{2\pi}{|4\pi|}=\frac{1}{2}\)
مثال از پیدا کردن ضابطۀ تابع
مثال 3: نمودار تابع \(\Large f \) با ضابطۀ \(\Large f(x)=a\cos bx+c\) در شکل زیر رسم شده است. مقادیر \(\Large a\) و \(\Large b\) و \(\Large c\) را به دست آورید.
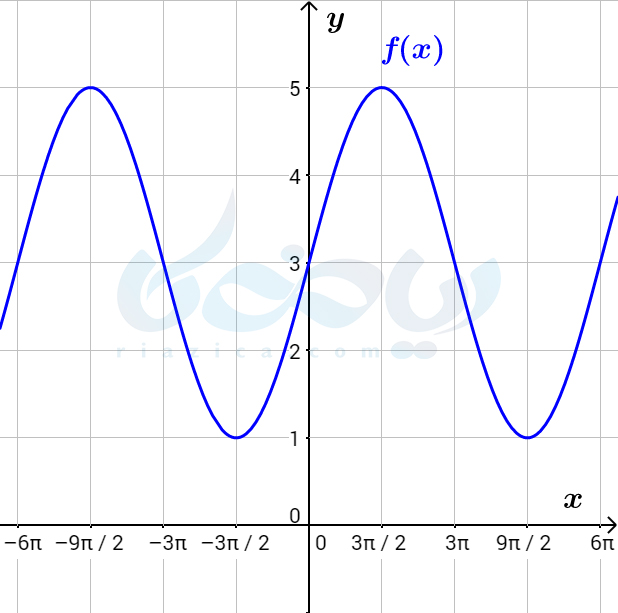
حل: همان طور که از نمودار تابع پیداست، دوره تناوب تابع برابر با \(\Large 6\pi\) است. بنابراین \(\Large \frac{2\pi}{|b|}\) برابر با \(\Large 6\pi\) است. پس \(\Large |b|\) برابر است با \(\Large \frac{1}{3}\). از طرفی مقدار ماکزیمم تابع برابر با \(\Large 5\) و مقدار مینیمم آن برابر با \(\Large 1\) است. بنابراین داریم:
\(\LARGE max=|a|+c=5\)
\(\LARGE min=-|a|+c=1\)
اگر معادلۀ اول و دوم را از یکدیگر کم کنیم، مقدار \(\Large 2|a|\) برابر با \(\Large 4\) به دست میآید:
\(\Large |a|+c-(-|a|+c)=4\)
پس، \(\Large |a|\) برابر با \(\Large 2\) است. اگر دو معادله را با یکدیگر جمع کنیم، مقدار \(\Large 2|c|\) برابر با \(\Large 6\) خواهد بود:
\(\Large |a|+c+(-|a|+c)=6\)
پس، \(\Large c\) برابر با \(\Large 3\) است. تا اینجا مقدار \(\Large c\) و \(\Large |a|\) و \(\Large |b|\) را به دست آوردیم. حال باید \(\Large a\) و \(\Large b\) را (بدون قدر مطلق) به دست آوریم. باید دقت کنیم، از آنجاییکه \(\Large \sin (-x)\) با \(\Large -\sin x\) برابر است، علامت کل عبارت \(\Large a \sin bx\) حائز اهمیت است نه \(\Large a\) و \(\Large b\) به تنهایی. یعنی به طور مثال تفاوتی ندارد که \(\Large a\) را منفی و \(\Large b\) را مثبت در نظر بگیریم یا \(\Large b\) را منفی و \(\Large a\) را مثبت در نظر بگیریم. در هر دو صورت یک منفی پشت عبارت \(\Large a \sin bx\) قرار میگیرد. برای به دست آوردن علامت عبارت \(\Large a \sin bx\) راههای متفاوتی وجود دارد. ساده ترین راه، امتحان کردن یک نقطه است. به طور مثال نقطۀ \(\Large (\frac{3\pi}{2},5)\) را روی نمودار در نظر میگیریم. مقدار \(\Large -2 \sin \frac{x}{3}+3\) برابر با \(\Large 1\) و مقدار \(\Large 2 \sin \frac{x}{3}x+3\) برابر با \(\Large 5\) است. پس، باید علامت مثبت پشت عبارت \(\Large 2 \sin \frac{3}{2}x\) قرار دهیم. در نتیجه \(\Large a\) و \(\Large b\) هر دو منفی و یا هر دو مثبت هستند و ضابطۀ تابع به صورت \(\Large 2 \sin \frac{x}{3}+3\) در میآید.
زنگ آخر کلاس دوره تناوب ریاضی دوازدهم تجربی
در این درسنامه که مربوط به ریاضی دوازدهم تجربی بود به بررسی مبحث دورۀ تناوب پرداختیم. همان طور که دیدید، ابتدا دورۀ تناوب و تابع متناوب را معرفی کردیم. سپس، تاثیر ضرایب مختلف و همچنین انتقال را در دورۀ تناوب و ماکزیمم و مینیمم نمودارهای سینوسی و کسینوسی بررسی کردیم. در آخر نیز دیدیم که با استفاده از روابطی که برای ماکزیمم و مینیمم و دورۀ تناوب توابع سینوسی و کسینوسی به دست آوردیم میتوان ضابطۀ برخی از توابع را به وسیلۀ نمودار آن ها مشخص کرد.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث دوره تناوب ریاضی دوازدهم تجربی دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





سلام تشکر از مطالب خیلی قشنگتون در رسم نمودار ها از چه برنامه ای استفاده میکنید اگر بفرمایید ممنون میشم.
سلام و عرض ادب
ممنون از انرژی و پیام پرمهرتون. از سایت های آنلاین رسم شکل کمک میگیریم.
موفق باشید
مچکرم
سلام و عرض ادب
خواهش میکنم.
سلام ممنون از مطلبی که گذاشته بودید ای کاش رسم منحنی از روی حداکثری و حداقلی و دوره تناوب رو هم توضیح بدید
با سلام وعرض ادب
برا تابع سینوس وکسینوس در پایه یازدهم به زودی قرار میدهیم
سلام . دوره تناوب توابع مثلثاتی وقتی توان می گیرند چند است ؟
سلام . سپاسگزارم از این همه مطالب قشنگ و توضیحات قابل فهم .میشه در مورد اینکه وقتی ماکسیمم و مینیمم و دوره تناوب تابع داده شده و ضابطه خواسته شده توضیح بدین . ممنونم .
با سلام وادب
دوست عزیز اگه خوب توابع مثلثاتی رو بشناسید واین پست روخونده باشید جواب واضحه از روی ماکسیمم ومینیمم تشخیص میدیم تابع سینوس هست یا کسینوس واندازه b روپیدا میکنیم واز روی دوره تناوب a رو پیدا میکنیم
سلام دوست عزیز مثال ۳ نمونه همین مطلب است
سلام یه سوالی داشتم.
دوره ی تناوب sin 2x (سینوس به توان دو ) ویا cos2x (کسینوس به توان 2 ) دوره ی تناوبشون رو از پی2/|b| یا پی/|b| استفاده کنیم منظورم اینه که توی صورت دوره تناوب های sin & cos از 2پی استفاده می شه ولی در sin & cos های به توان دو از پی استفاده می شه؟؟؟؟
ممنون اگه ن بدین.
بله درسته دوست عزیز
در تابع |y=|sinxدوره تناوب چی میشه؟
با سلام وادب
دوره تناوبش پی میشود
دوره تناوب دوتا سینوس دو ایکس
با سلام وادب
اگه درسنامه بالا رومطالعه کنید به جواب میرسید که میشود عدد پی
عالی بود توضیحات سپاس فراوان
سلام( cos(4x متناوب ؟؟؟
با سلام منظورتون دوره تناوب هست?
درود بر شما.
بسیار عالی
کامل و قابل درک توضیح دادید
با سلام
خدا رو شکر مفید بوده
سلام وقتتون بخیر
ببخشید دوره تناوب :
sin⁴ 2x + cos⁴ 2x
چنده ؟
اگه میشه راه حلش رو هم توضیح بدین.
ممنون!!
سلام وقتتون بخیر
ببخشید دوره تناوب
sin⁴ 2x + cos⁴ 2x
رو با چ فرمولی باید محاسبه کنیم؟
ممنون
سلام وقتتون بخیر
ببخشید دوره تناوب
sin⁴ 2x + cos⁴ 2x
رو با هم چگونه و با چه فرمولی باید محاسبه کنیم؟
خیلی ممنونم