حجم و سطح ریاضی هفتم 💎📦 – دورانش بده!

در درسنامهٔ حجم و سطح ریاضی هفتم می‌خواهیم با دوران اشکال مختلف حول یک محور، حجم‌های مختلفی به وجود آوریم. در کنار این مبحث، به مباحث جانبی از قبیل ساخت استوانه با یک مستطیل در دو حالت مختلف و نگاه به حجم‌ها از زوایای مختلف نیز خواهیم پرداخت. با ما تا انتهای درسنامهٔ حجم و سطح ریاضی هفتم همراه باشید.

ساخت استوانه با مستطیل

همان طور که در درسنامهٔ مساحت جانبی و کل ریاضی هفتم دیدید، شکل گستردهٔ یک استوانه، یک مستطیل به همراه دو دایره‌ است. دایره‌ها قاعده‌های استوانه را تشکیل می‌دهند. در واقع اگر یک صفحهٔ مستطیل شکل داشته باشیم و دو سر مستطیل را به صورت زیر به هم بچسبانیم، یک استوانه (بدون در نظر گرفتن قاعده‌ها) تشکیل می‌شود.

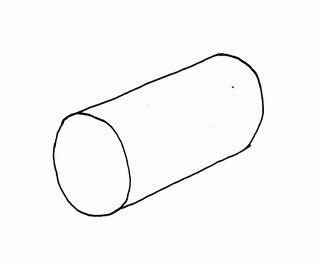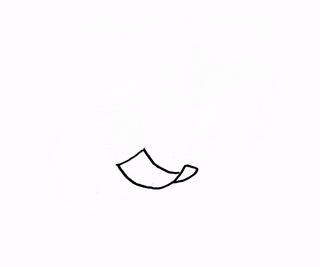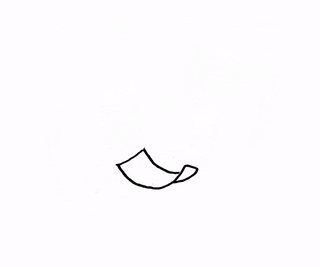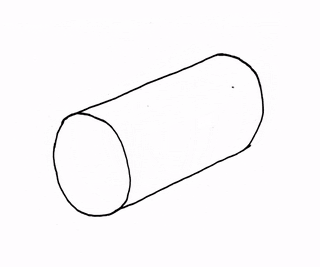
بسته به اینکه طول‌های مستطیل را به هم بچسبانیم یا عرض‌های آن را، دو استوانه با ابعاد متفاوت و در نتیجه حجم‌های مختلف تشکیل می‌شود. برای اینکه بهتر متوجه شوید، به مثال بعدی از درسنامهٔ حجم و سطح ریاضی هفتم توجه کنید.

مثال از ساخت مستطیل با استوانه

دو شکل زیر را در نظر بگیرید:

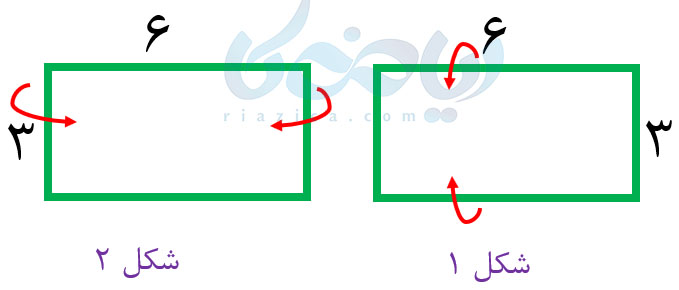
در هر دو شکل، با یک مستطیل سر و کار داریم. در شکل \(\Large 1\)، طول‌های مستطیل را به هم می‌چسبانیم. در شکل \(\Large 2\)، عرض‌های مستطیل را به هم می‌چسبانیم. در این صورت، استوانه‌های زیر به وجود می‌آیند:

همان طور که در درسنامهٔ محاسبه حجم های منشوری هفتم خواندیم، حجم هر منشور برابر است با حاصل ضرب مساحت قاعده در ارتفاع. برای محاسبهٔ مساحت قاعدهٔ استوانه، نیاز به دانستن شعاع قاعدهٔ آن داریم. بنابراین ابتدا باید شعاع قاعدهٔ هر استوانه را محاسبه کرده و سپس حجم آن را به دست آوریم. ابتدا قاعدهٔ استوانهٔ اول را محاسبه کنیم. محیط قاعدهٔ استوانهٔ اول برابر است با عرض مستطیل. بنابراین داریم:

\(\LARGE 2 \times \pi r=3\)

برای ساده شدن محاسبات، مقدار \(\Large \pi\) را برابر با \(\Large 3\) در نظر می‌گیریم. در این صورت اندازهٔ شعاع برابر است با:

\(\LARGE r=\frac{3}{2 \times \pi} = \frac{3}{2 \times 3} = \frac{1}{2}\)

در نتیجه حجم استوانهٔ اول به صورت زیر به دست می‌آید:

\(\LARGE V_1=\pi r^2h=3 \times \frac{1}{4} \times 6 =\frac{9}{2} \)

برای محاسبهٔ حجم استوانهٔ دوم نیز باید همین کار را انجام دهیم. ابتدا شعاع قاعدهٔ استوانهٔ دوم را محاسبه کنیم. محیط قاعدهٔ استوانهٔ دوم برابر است با طول مستطیل. بنابراین داریم:

\(\LARGE 2 \times \pi r=6\)

برای ساده شدن محاسبات، مقدار \(\Large \pi\) را برابر با \(\Large 3\) در نظر می‌گیریم. در این صورت اندازهٔ شعاع برابر است با:

\(\LARGE r=\frac{6}{2 \times \pi} = \frac{6}{2 \times 3} = 1\)

در نتیجه حجم استوانهٔ دوم به صورت زیر به دست می‌آید:

\(\LARGE V_1=\pi r^2h=3 \times 1 \times 3 =9 \)

همان طور که دیدید، با اینکه مستطیل اولیه یکی بود اما حجم‌ها مختلفی به دست آوردیم. می‌توان ثابت کرد که همیشه نسبت حجم استوانهٔ اول به حجم استوانهٔ دوم برابر است با نسبت عرض به طول مستطیل. در اینجا عرض مستطیل برابر با نصف طول مستطیل بود بنابراین حجم استوانهٔ اول نیز نصف حجم استوانهٔ دوم شد.

ساخت حجم با دوران

با دوران یک سطح حول یک محور (خط) می‌توان یک حجم به دست آورد. برای اینکه بهتر متوجه شوید، در ادامهٔ درسنامهٔ حجم و سطح ریاضی هفتم ، سطوح مختلف را حول محورهای مختلف دوران داده و حجم‌های حاصل را بررسی می‌کنیم.

دوران مستطیل حول یک ضلع

اگر یک مستطیل را حول یک محور (خط) که بر یکی از اضلاعش منطبق است، دوران دهیم یک استوانه تشکیل می‌شود. شکل زیر را در نظر بگیرید:

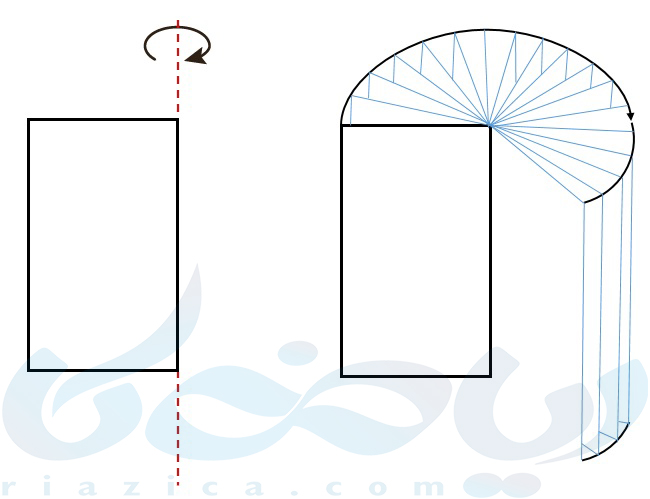
تصویر متحرک زیر نیز به تجسم بهتر شما در این مبحث از درسنامهٔ حجم و سطح ریاضی هفتم کمک می‌کند:

باز هم بسته به اینکه مستطیل را حول کدام یک از اضلاعش دوران دهیم، حجم‌های مختلفی به دست می آید. برای اینکه بهتر متوجه شوید، به مثال بعدی از درسنامهٔ حجم و سطح ریاضی هفتم توجه کنید.

مثال از دوران مستطیل و ساخت استوانه

مثال 1: یک مستطیل با ابعاد زیر را یک بار حول عرض و بار دیگر حول طول دوران می‌دهیم. در هر حالت، حجم استوانهٔ تشکیل شده را به دست آورید.

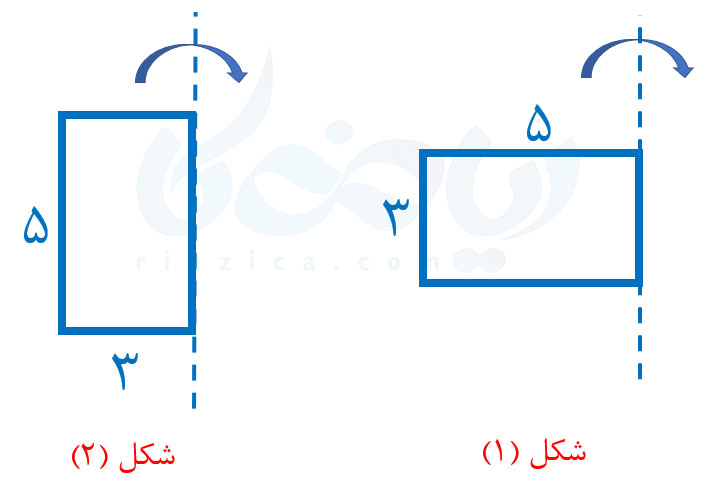
حل: در شکل \(\Large 1\)، شعاع قاعدهٔ استوانه برابر است با طول مستطیل؛ یعنی برابر است با \(\Large 5\). ارتفاع استوانه نیز برابر است با عرض مستطیل؛ یعنی برابر است با \(\Large 3\). در نتیجه حجم استوانهٔ شکل \(\Large 1\) به صورت زیر به دست می‌آید (برای ساده شدن محاسبات، مقدار \(\Large \pi\) را برابر با \(\Large 3\) در نظر می‌گیریم):

\(\LARGE V_1=\pi r^2 h\)

\(\LARGE =3 \times 25 \times 3=225\)

در شکل \(\Large 2\)، شعاع قاعدهٔ استوانه برابر است با عرض مستطیل؛ یعنی برابر است با \(\Large 3\). ارتفاع استوانه نیز برابر است با طول مستطیل؛ یعنی برابر است با \(\Large 5\). در نتیجه حجم استوانهٔ شکل \(\Large 2\) برابر است با :

\(\LARGE V_2=\pi r^2 h\)

\(\LARGE =3 \times 9 \times 5=135\)

همان طور که دیدید، بسته به اینکه دوران حول چه محوری صورت گیرد، حجم‌های مختلفی به دست می‌آید. در این مورد نیز می‌توان ثابت کرد که همیشه نسبت حجم استوانهٔ اول به حجم استوانهٔ دوم برابر است با نسبت طول به عرض مستطیل. در اینجا نسبت طول به عرض مستطیل برابر با \(\Large \frac{5}{3}\) بود، نسبت حجم استوانهٔ اول به دوم نیز برابر با \(\Large \frac{5}{3}\) شد.

نکته : نسبت حجم این دو استوانه به یکدیگر برابر نسبت طول به عرض می باشد.

نکته : نسبت مساحت کل این دو استوانه به یکدیگر نیز برابر نسبت طول به عرض می باشد.

نکته : مساحت جانبی این دو استوانه با هم برابر است.

مثال از درسنامهٔ حجم و سطح ریاضی هفتم

همان طور که دیدید، با دوران یک سطح حول یک محور در فضا، حجم تشکیل شد. به غیر از مستطیل می‌توانیم این کار را برای سطوح دیگر نیز انجام دهیم. در صورتی که یک مثلث قائم‌الزاویه را حول قاعدهٔ آن دوران دهیم، یک مخروط تشکیل می‌شود. به شکل زیر دقت کنید:

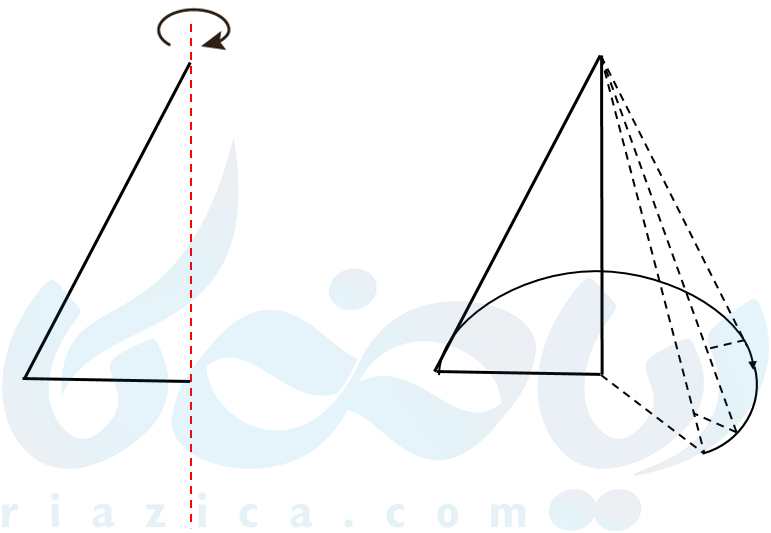
تصویر متحرک زیر نیز به تجسم بهتر شما کمک می‌کند:

مثال از درسنامهٔ حجم و سطح ریاضی هفتم

می‌توانیم یک نیم‌دایره را حول قطر آن دوران دهیم. در این صورت، همان طور که در شکل زیر می‌بینید، یک کره به دست خواهد آمد:

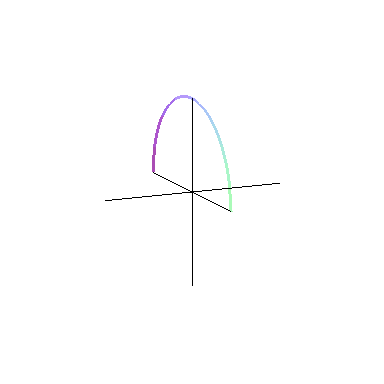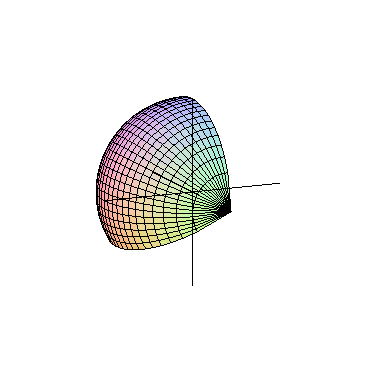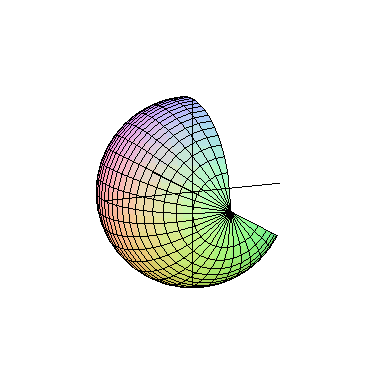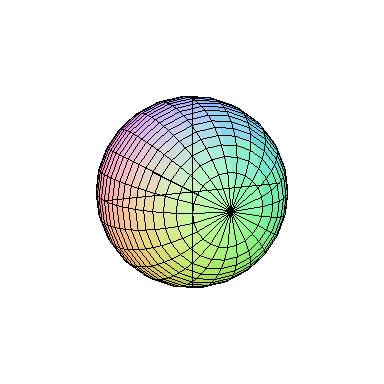
دوران شکل دلخواه در درسنامهٔ حجم و سطح ریاضی هفتم

لزومی ندارد که همیشه شکل‌های متداول در هندسه مانند مستطیل، مثلث یا دایره را دوران دهیم. هر سطح دلخواهی را می‌توان حول یک محور دوران داد و یک حجم دلخواه به دست آورد. در شکل زیر می‌توانید حجم حاصل از دوران یک سطح دلخواه حول یک محور را ببینید:

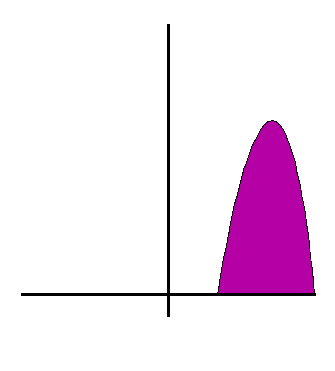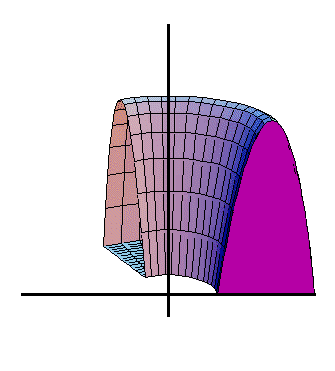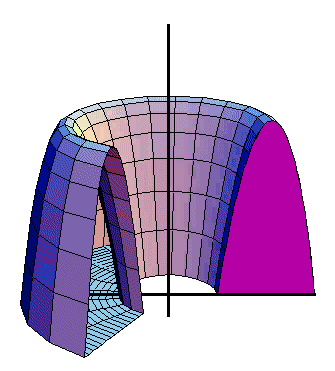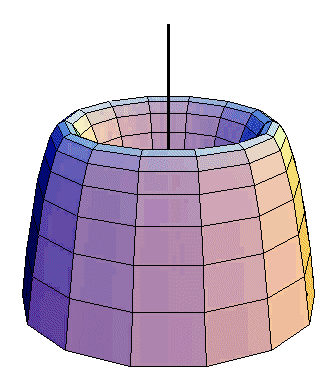
تفاوتی که دوران شکل بالا با شکل های قبلی درسنامه حجم و سطح ریاضی هفتم دارد، فاصلهٔ بین شکل و محور دوران است. در شکل‌های قبلی، سطح دلخواهمان را حول محوری منطبق بر یکی از اضلاع دوران می‌دادیم. اما همان طور که در شکل بالا می‌بینید، لزومی ندارد که سطح و محور، بدون فاصله باشند. در تصویر متحرک زیر می‌توانید دوران شکل دلخواه دیگری را حول محور مشاهده کنید.

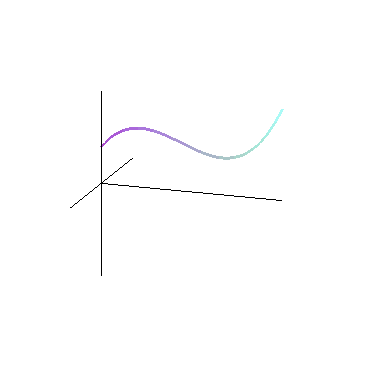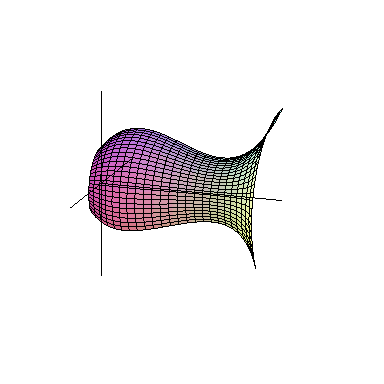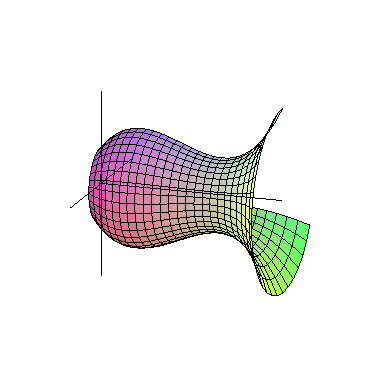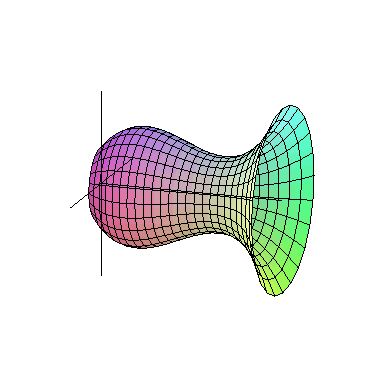
با حرکت یک سطح در فضا حجم ساخته می شود.

به قسمت بعدی از درسنامهٔ حجم و سطح ریاضی هفتم توجه کنید.

نگاه به حجم‌ها از زوایای مختلف

می‌توان به حجم‌های هندسی مختلف، از زوایای گوناگون نگاه کرده و شکل دیده شده را رسم کرد. مثلاً اگر از بالا به یک مکعب نگاه کنیم، یک مربع می‌بینیم. در تصویر متحرک زیر، ابتدا نمای سه بعدی جسم را دیده و سپس به آن از بالا نگاه می‌کنیم:

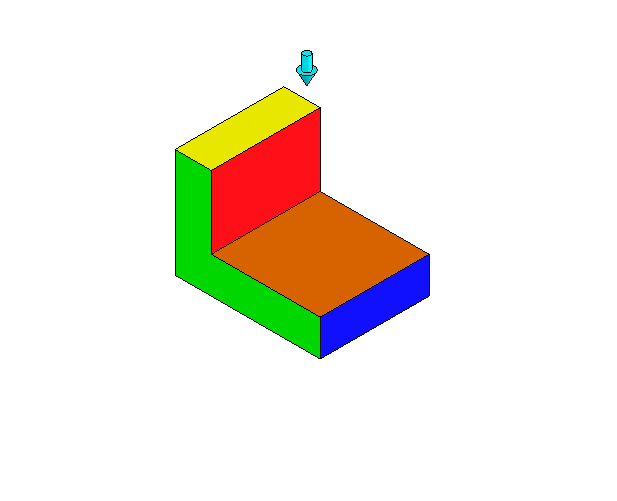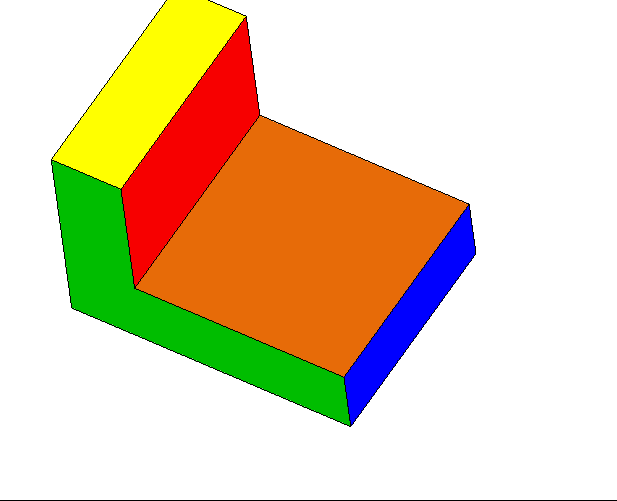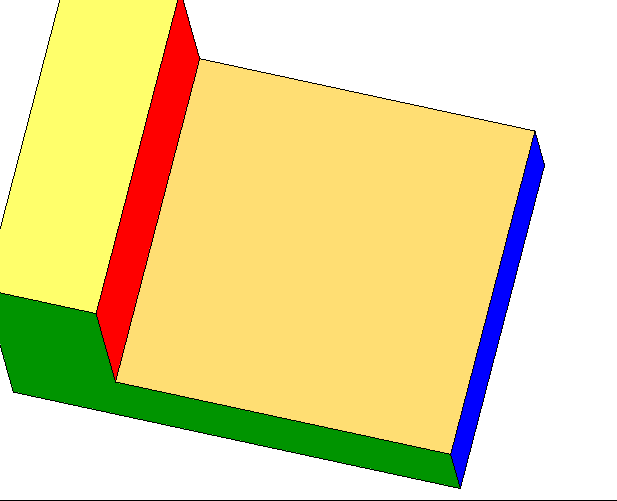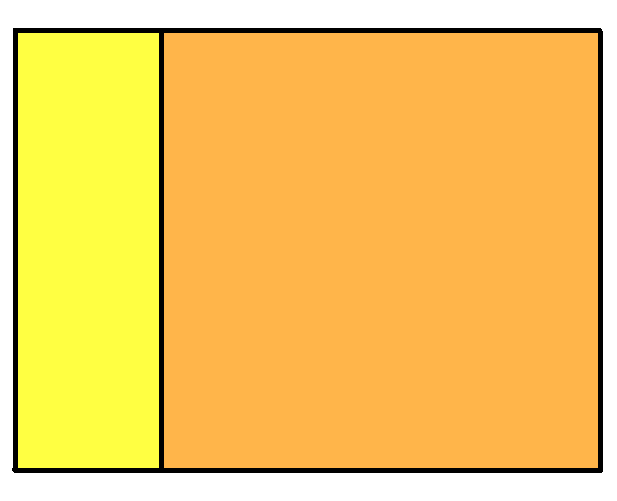
اگر به همین جسم از روبه‌رو نگاه کنیم، شکل زیر حاصل می‌شود:

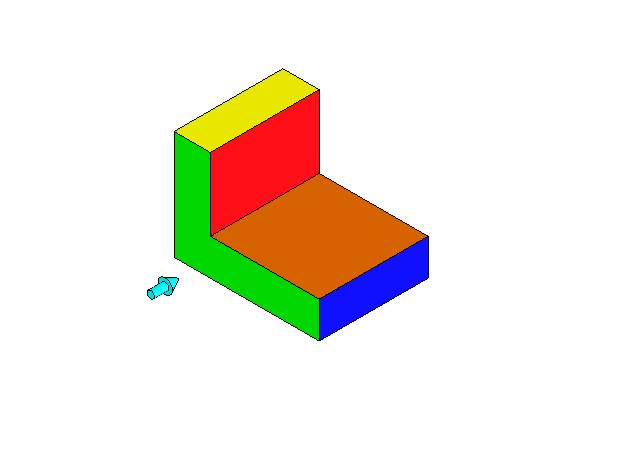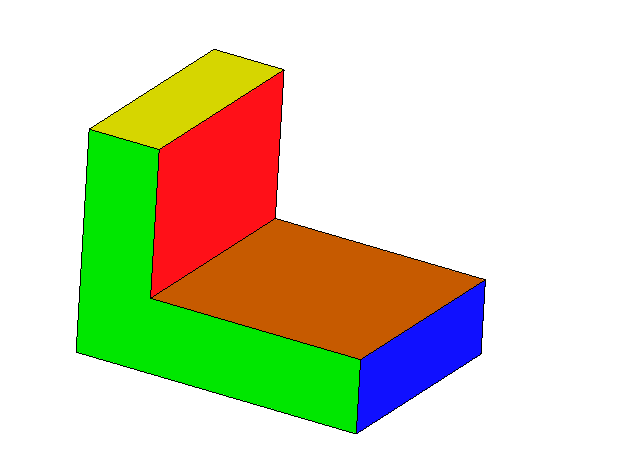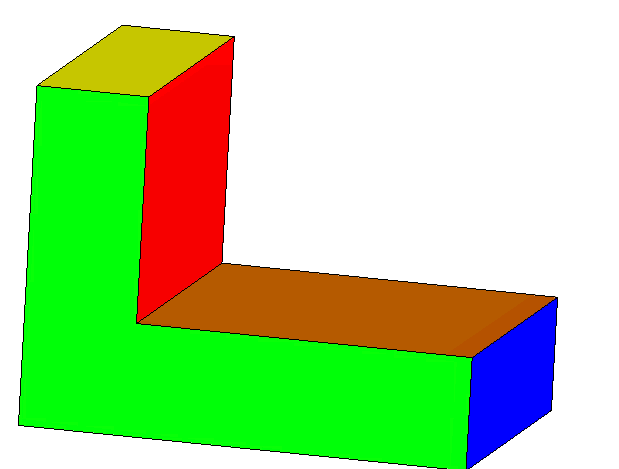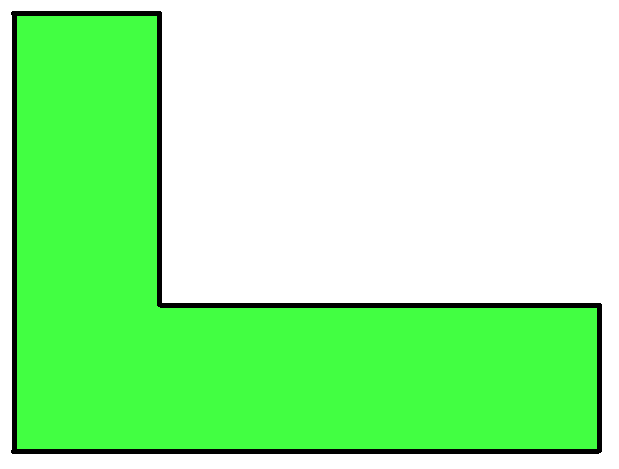
برای یادگیری مطالب بیشتر در این رابطه به پست حجم وسطح ریاضی نهم را مطالعه کنید

زنگ آخر کلاس حجم و سطح ریاضی هفتم

در درسنامه‌ای که از ریاضی هفتم خواندیم، دیدیم که با دوران اشکال مختلف حول یک محور (خط) می‌توان حجم‌های مختلفی به دست آورد. در کنار این مبحث، ساخت استوانه از یک مستطیل و همچنین نگاه به حجم‌ها از زوایای مختلف را بررسی کردیم.

ما در ریاضیکا آماده‌ی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با معادله خط ریاضی نهم دارید، در دیدگاه‌ها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند ‌داد.