آشنایی با اثبات در هندسه نهم ??‍⚖️ – استدلالش کن!

در درسنامۀ آشنایی با اثبات در هندسه نهم ابتدا به دو سؤال زیر پاسخ می‌دهیم:

• فرض و حکم یک مسئله چه چیزهایی هستند؟
• تعمیم نتیجۀ یک استدلال چیست و چه کاربردی دارد؟

بعد از پاسخ به این دو سؤال، برخی از اشتباهات رایج در اثبات مسائل هندسی را با هم بررسی کرده و دلیل غلط بودن هر اثبات را بررسی می‌کنیم. مثال‌هایی که با یکدیگر حل خواهیم کرد، کمک زیادی در درک مبحث می‌کند. پس با ما تا انتهای درسنامه همراه باشید.

فرض و حکم در آشنایی با اثبات در هندسه نهم

همیشه برای حل یک مسئلۀ ریاضی، اولین گام، شناخت صحیح فرض و حکم مسئله است. اما فرض و حکم چیستند؟ به زبان ساده، فرض یک مسئله همان اطلاعاتی است که مسئله برای حل به ما داده است. حکم مسئله نیز همان خواستۀ مسئله از ماست. برای اینکه بهتر متوجه شوید، به مثال زیر از مبحث آشنایی با اثبات در هندسه نهم دقت کنید.

مثال از تعیین فرض و حکم مسئله

مثال 1: در مسئلۀ زیر، فرض و حکم را مشخص کنید.

مسئله: در شکل زیر، نقطۀ \( \Large M\) روی نیمساز زاویۀ \( \Large A\) قرار دارد. ثابت کنید فاصلۀ نقطۀ \( \Large M\) از دو ضلع زاویۀ \( \Large A\) به یک اندازه است.

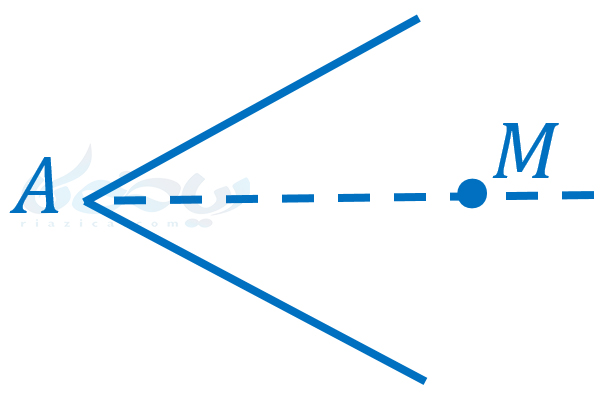
حل: اطلاعاتی که مسئله به ما داده این است که نقطۀ \( \Large M\) روی نیمساز زاویۀ \( \Large A\) قرار دارد. خواستۀ مسئله از ما این است که ثابت کنیم فاصلۀ نقطۀ \( \Large M\) از دو ضلع زاویۀ \( \Large A\) به یک اندازه است. بنابراین با توجه به توضیحی که در مورد فرض و حکم دادیم، فرض و حکم این مسئله به صورت زیر است:

مثال 2: در مسئلۀ زیر، فرض و حکم را مشخص کنید.

مسئله: نشان دهید نقاط روی عمود منصف یک پاره‌خط، از دو سر پاره‌خط به یک انداره‌اند.

حل: نوع بیان این مسئله با مسئلۀ قبلی کمی متفاوت است اما باز هم با توجه به نکته‌ای که گفتیم می‌توانیم فرض و حکم را مشخص کنیم. اطلاعاتی که مسئله به ما داده این است که نقاطی روی عمود منصف یک پاره‌خط دلخواه وجود دارند. خواستۀ مسئله از ما این است که ثابت کنیم فاصلۀ هر کدام از این نقاط از دو سر پاره‌خط به یک اندازه است. بنابراین فرض و حکم مسئله به صورت زیر است:

مثال 3: در مسئلۀ زیر، فرض و حکم را مشخص کنید.

مسئله: ثابت کنید در هر مثلث مجموع زوایا برابر با 180 درجه است.

حل: اطلاعاتی که این مسئله به ما داده است، از مسئلۀ قبل نیز کمتر است. در واقع در این مسئله تنها می‌دانیم که یک مثلث دلخواه داریم. خواستۀ مسئله از ما این است که ثابت کنیم مجموع زوایای این مثلث دلخواه برابر با 180 درجه است. بنابراین فرض و حکم این مسئله به صورت زیر است:

تعمیم نتیجه در آشنایی با اثبات در هندسه نهم

بحث مهم بعدی در درس آشنایی با اثبات در هندسه نهم تعمیم نتیجۀ حاصل از استدلال است. گاهی در استدلالی که برای یک مسئله به کار می‌بریم، از فرض ها یا ویژگی‌هایی استفاده می‌کنیم که برای مسائل مشابهِ دیگر نیز تنها به همان فرض‌ها یا ویژگی‌ها نیاز داریم. بنابراین می‌توانیم نتیجه‌ای که از آن استدلال گرفتیم را به مسائل دیگر نیز تعمیم دهیم. برای اینکه بهتر متوجه شوید، به مثال‌های زیر از درسنامۀ آشنایی با اثبات در هندسه نهم دقت کنید.

مثال از تعمیم نتیجه

مثال 4: در شکل زیر، مثلث \( \Large ABC\) متساوی‌الاضلاع است. \( \Large AD\) نیمساز زاویۀ \( \Large A\) است. ثابت کنید \( \Large AD\) میانه است. آیا می‌توانیم بدون اینکه اثبات را بازنویسی کنیم، نتیجه بگیریم نیمساز‌های زوایای \( \Large B\) و \( \Large C\) نیز میانه‌اند؟

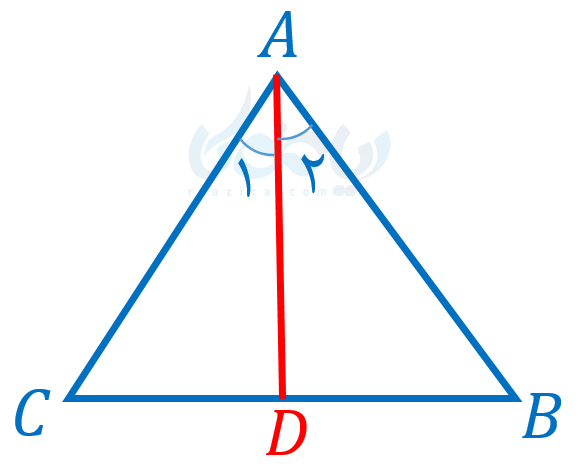
حل: ابتدا به صورت زیر ثابت می‌کنیم مثلث‌های \( \Large ABD\) و \( \Large ACD\) هم‌نهشت هستند (در صورتی که هم‌نهشتی مثلث‌ها را فراموش کرده‌اید، درسنامۀ مثلث‌های هم‌نهشت را مطالعه کنید):

بنابراین \( \Large BD=CD\). در نتیجه \( \Large AD\) میانه است. اما به قسمت اصلی سوال بپردازیم. آیا می‌توانیم بدون بازنویسی اثبات، نتیجه بگیریم نیمساز‌های زوایای \( \Large B\) و \( \Large C\) نیز میانه‌اند؟ برای اثبات میانه بودن \( \Large AD\) تنها از برابری اضلاع \( \Large AB\) و \( \Large AC\) و برابری زوایای \( \Large A_1\) و \( \Large A_2\) استفاده کردیم. نیمساز هم که در هر صورتی مشترک است پس چون تمام ضلعهای مثلث متساوی الاضلاع با هم برابرهستند،بنابراین اگر نیمساز زوایای دیگر را نیز در نظر بگیریم می‌توانیم میانه بودن آن‌ها را نتیجه گیری کنیم. دقت کنید همیشه نمی‌توان نتایج را به این صورت تعمیم داد. به مثال بعدی از درسنامۀ آشنایی با اثبات در هندسه نهم دقت کنید.

مثال از تعمیم نادرست نتیجه

مثال 5: فرض کنید در مثال 2 به جای مثلث متساوی‌الاضلاع، مثلث متساوی الساقین داشتیم. یعنی فرض کنید در شکل زیر، مثلث \( \Large ABC\) متساوی‌الساقین است. ثابت کنید \( \Large AD\) میانه است. آیا این بار هم می‌توانیم بدون اینکه اثبات را بازنویسی کنیم، نتیجه بگیریم نیمساز‌های زوایای \( \Large B\) و \( \Large C\) نیز میانه‌اند؟

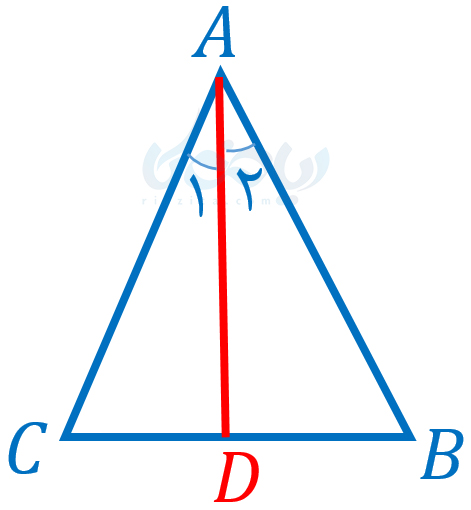
حل: ابتدا با استفاده از هم‌نهشتی مثلث‌های \( \Large ABD\) و \( \Large ACD\) ثابت می‌کنیم \( \Large AD\) میانه است:

بنابراین \( \Large BD=CD\). در نتیجه \( \Large AD\) میانه است. اما این بار نمی‌توانیم این نتیجه را به نیمساز دیگر زوایا نیز تعمیم دهیم. یعنی نمی‌توانیم بگوییم نیمساز‌های زوایای \( \Large B\) و \( \Large C\) نیز میانه‌اند. زیرا برای اثبات میانه بودن \( \Large AD\) از برابری اضلاع \( \Large AB\) و \( \Large AC\) استفاده کردیم. اما برای زوایای دیگر، برابری مشابه نداریم. یعنی به طور مثال نیمساز زاویۀ \( \Large B\) که در شکل زیر با \( \Large BM\) مشخص شده است را در نظر بگیرید:

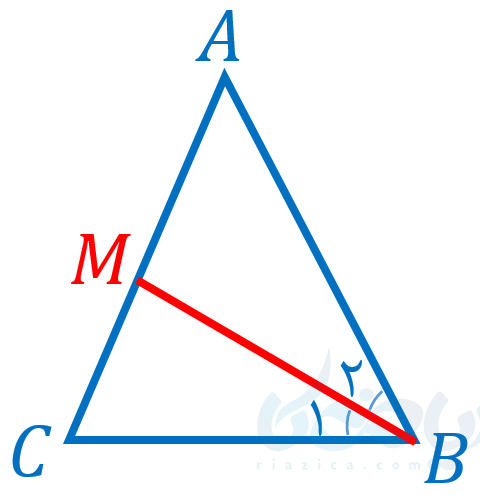
در این حالت، دیگر اضلاع \( \Large AB\) و \( \Large BC\) برابر نیستند و نمی‌توانیم هم‌نهشتی مثلث‌های \( \Large ABM\) و \( \Large BCM\) را اثبات کنیم. بنابراین باید در تعمیم نتایج یک مسئله کاملاً با دقت عمل کنیم.

بررسی اثبات‌های معتبر و نامعتبر

مبحث آخر از درسنامۀ آشنایی با اثبات در هندسه نهم بررسی اثبات‌های معتبر و نامعتبر است. به طور کلی اشکالات مختلفی وجود دارند که می‌توانند باعث نامعتبر شدن یک استدلال  یا اثبات شوند. در درسنامۀ استدلال ریاضی نهم برخی از آن‌ها را دیدیم. در این جا نیز بعضی از آن‌ها را بررسی می‌کنیم تا مراقب باشیم در اثباتمان دچار این اشتباه‌ها نشویم. در هر یک از قسمت‌های بعدی از درسنامۀ آشنایی با اثبات در هندسه نهم یکی از این اشتباهات را بررسی ‌می‌کنیم.

اثبات با اندازه‌گیری

به هیچ عنوان نمی‌توانیم با اندازه‌گیری ابعاد یک شکل، حکم یک مسئله را ثابت کنیم. به طور مثال فرض کنید از ما خواسته شده ثابت کنیم که قطرهای متوازی‌الاضلاع یکدیگر را نصف می‌کنند. نمی‌توانیم چند متوازی الاضلاع رسم کنیم و با اندازه گیری اقطار هر یک، خواستۀ مسئله را نتیجه گیری کنیم زیرا هم شخص اندازه گیری کننده وهم وسیله اندازه گیری دارای خطا هستند.

اثبات برای حالت خاص

یکی دیگر از اشتباهاتی که در درسنامۀ آشنایی با اثبات در هندسه نهم آن را بررسی می‌کنیم، اثبات حکم برای یک حالت خاص است. فرض کنید از ما خواسته شده که ثابت کنیم در هر مثلث، اندازۀ زاویۀ خارجی برابر است با مجموع دو زاویۀ داخلی غیر مجاور. یک اثبات غلط این است که مثلث متساوی‌الاضلاع \( \Large ABC\) که در شکل زیر رسم شده است را در نظر بگیریم:

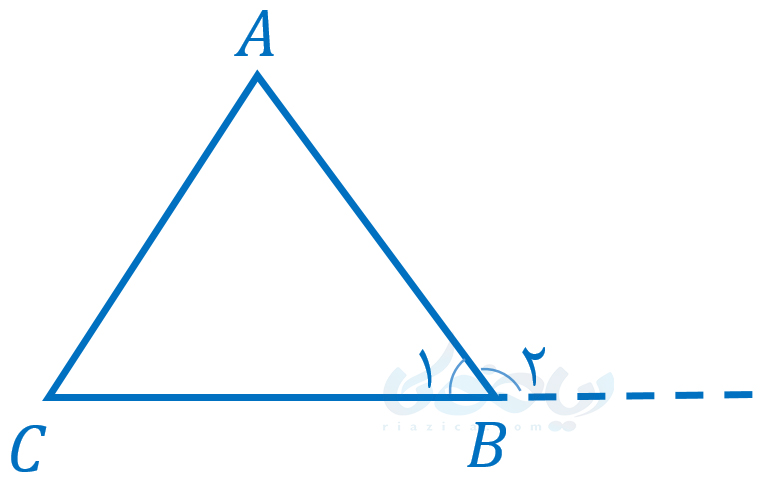
آنگاه بگوییم چون اندازۀ هر زاویه در مثلث متساوی‌الاضلاع برابر با 60 درجه است، بنابراین زاویۀ \( \Large B_1\) برابر با 60 درجه بوده و زاویۀ \( \Large B_2\) برابر با 120 درجه است. از آنجاییکه اندازۀ \( \Large A\) و \( \Large C\) هم هر کدام برابر با 60 درجه است، پس داریم:

\( \LARGE B_2=A+C\)

اما اثبات ما کاملاً اشتباه است. در مسئله از ما خواسته شده که یک حکم را برای هر مثلث ثابت کنیم، اما ما تنها این حکم را برای مثلث متساوی‌الاضلاع ثابت کرده‌ایم. در واقع به جای اینکه حکم را ثابت کنیم، آن را تنها برای یک حالت خاص ثابت کرده‌ایم. لذا اثبات ما درست نیست.

استنتاج غلط از نظر منطقی

اشتباه دیگری که در درسنامۀ آشنایی با اثبات در هندسه نهم بررسی می‌کنیم، استنتاج غلط از نظر منطقی است. یعنی در اثباتمان از یک نتیجه گیری که با توجه به منطق ریاضی غلط است، استفاده کنیم. برای اینکه بهتر متوجه شوید، مثال زیر را در نظر بگیرید.

مثال 6: کدام یک از دو نتیجه گیری زیر اشتباه است؟

1. در هر متوازی‌الاضلاع، قطرها یکدیگر را نصف می‌کنند. در نتیجه، در هر لوزی نیز قطرها یکدیگر را نصف می‌کنند.
2. در هر لوزی قطرها بر یکدیگر عمود هستند. در نتیجه، در هر متوازی الاضلاع قطرها بر یکدیگر عمود هستند.

حل: نتیجه گیری 1 درست است. زیرا هر لوزی یک متوازی‌الاضلاع است. چون در هر متوازی‌الاضلاع قطرها یکدیگر را نصف می‌کنند، پس در لوزی هم که نوعی متوازی الاضلاع است قطرها یکدیگر را نصف می‌کنند. اما نتیجه گیری 2 اشتباه است. هر متوازی الاضلاع یک لوزی نیست. بنابراین نمی‌توانیم نتیجه گیری کنیم در هر متوازی الاضلاع نیز قطرها بر هم عمود هستند.

زنگ آخر کلاس آشنایی با اثبات در هندسه نهم

به پایان این درسنامه رسیدیدم. با یکدیگر تعریف فرض و حکم یک مسئله را بررسی کردیم. دیدیم که در چه شرایطی می‌توان نتیجۀ حاصل از یک استدلال را به مسائل مشابه تعمیم داد. همچنین، به بررسی چند حالت از اشتباهات متداول در اثبات‌های هندسی پرداختیم و دلایل نادرست بودن هر یک را بیان کردیم.

ما در ریاضیکا آماده‌ی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث آشنایی با اثبات در هندسه نهم دارید، در دیدگاه‌ها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند ‌داد.