آموزش ریاضی پایه نهم
حل مسئله در هندسه نهم 4️⃣⚜️ – ۴ گام طلایی!
در درسنامۀ حل مسئله در هندسه نهم میخواهیم گامهای حل مسائل هندسی را با یکدیگر مرور کنیم. اگرچه نمیتوان یک روش کلی برای حل مسائل هندسی ارائه داد، اما میتوان یک چارچوب کلی برای حل آنها ترسیم کرد تا به کمک آن، آسانتر و سریعتر به پاسخ رسید. ابتدا این گامها را به صورت خلاصه بیان میکنیم. سپس در حل مثال، مطابق با این گامها جلو خواهیم رفت.
گامهای حل مسئله در هندسه نهم
با توجه به کتاب درسی، چهار گام به صورت زیر برای حل مسائل هندسی وجود دارد:
- خواندن صورت مسئله و تشخیص مفاهیم آن (باید تمامی مفاهیم مربوط به مسئله را، از سالهای گذشته تا کنون بشناسیم. به طور مثال اگر با دایره سر و کار داریم، ویژگیهای دایره را بشناسیم و بر آن مسلط باشیم)
- رسم شکل مناسب در صورت نیاز
- تشخیص فرض و حکم (بهتر است فرض و حکم را بنویسیم)
- پیدا کردن راه حل برای رسیدن از فرض به حکم
در ادامۀ درسنامۀ حل مسئله در هندسه نهم سعی میکنیم مثالهای مختلفی حل کرده و در هر کدام، گامهایی که ذکر کردیم را طی کنیم.
برابری کمانهای یک دایره
مثال 1: در شکل زیر کمانهای \(\Large AB\) و \(\Large CD\) با هم برابرند. ثابت کنید وترهای \(\Large AB\) و \(\Large CD\) نیز با یکدیگر برابرند.
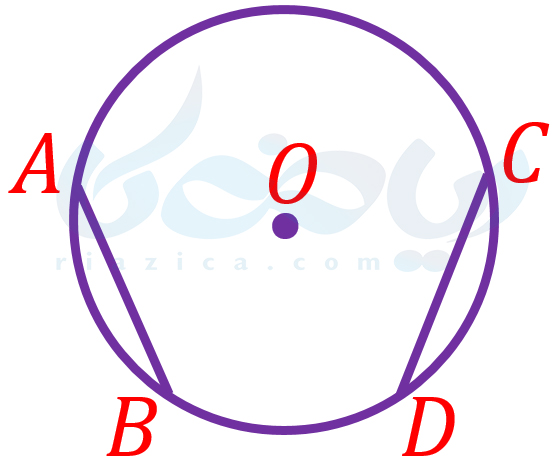
حل: بهترین روش برای حل این مسئله، رسم شعاعهای \(\Large OA\) و \(\Large OB\) و \(\Large OC\) و \(\Large OD\) و اثبات هم نهشتی مثلثهای \(\Large OAB\) و \(\Large OCD\) است. حال بیایید مطابق با چهار گامی که گفتیم پیش برویم. در گام اول، صورت مسئله را میخوانیم. در این مسئله با مفاهیمی مثل دایره، وتر دایره، برابری وترهای دایره و برابری کمانهای دایره سر و کار داریم. در گام دوم، شکل مسئله را تکمیل میکنیم. از آنجایی که می خواهیم با اثبات هم نهشتی مثلثهای \(\Large OAB\) و \(\Large OCD\)، برابری وترهای \(\Large AB\) و \(\Large CD\) را اثبات کنیم، خطوط اضافۀ زیر را که با خط چین مشخص شده است رسم میکنیم:
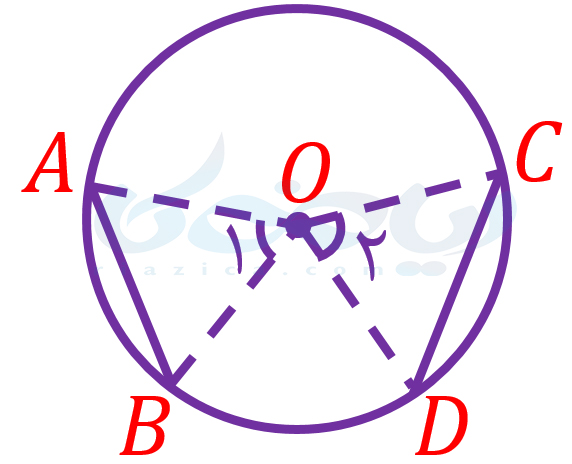
به یاد داشته باشید که برای حل مسائل هندسی دیگر نیز میتوانیم مانند این مسئله خطوط اضافهای را رسم کرده و بدون لطمه زدن به استنتاج منطقی، فرضهایی را اضافه کنیم. در گام سوم حل مسئله در هندسه نهم ، فرض و حکم مسئله را مشخص میکنیم. فرض مسئله این است که کمانهای \(\Large AB\) و \(\Large CD\) با هم برابرند. خواستۀ مسئله که همان حکم مسئله است، اثبات برابری وترهای \(\Large AB\) و \(\Large CD\) است. فرض و حکم را در جدولی به شکل زیر نشان میدهیم:
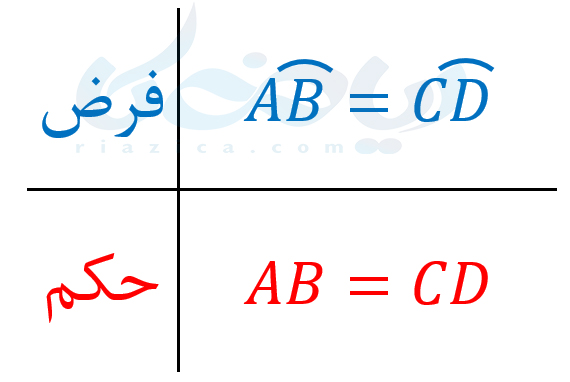
در گام چهارم، راه حل مناسب برای رسیدن از فرض به حکم را پیدا میکنیم. همانطور که گفتیم، از اثبات هم نهشتی مثلثهای \(\Large OAB\) و \(\Large OCD\)، برابری وترهای \(\Large AB\) و \(\Large CD\) را ثابت میکنیم. باید یادآوری کنیم که زوایای رو به رو به کمانهای برابر، با یکدیگر برابر هستند. با توجه به این مسئله، برای اثبات همنهشتی مثلثهای \(\Large OAB\) و \(\Large OCD\) به صورت زیر عمل میکنیم:
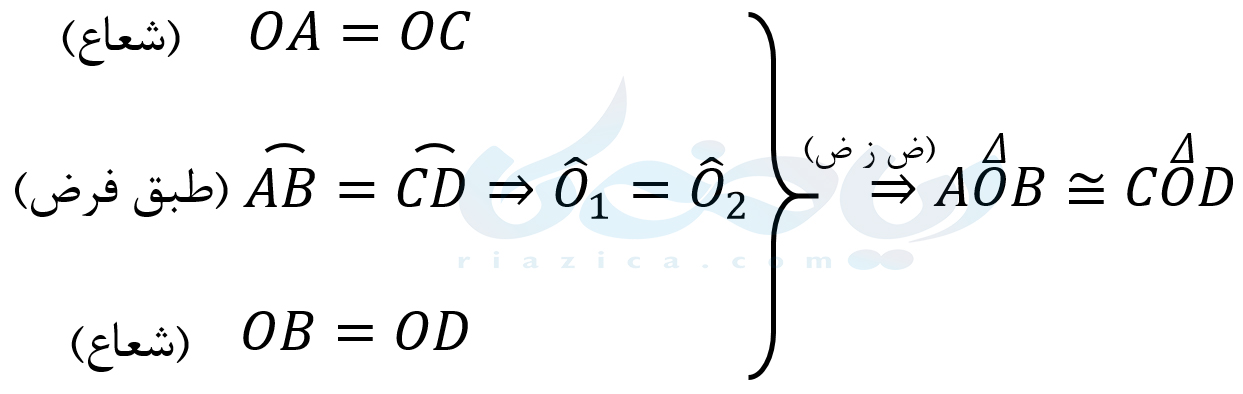
با توجه به این همنهشتی، تساویهای زیر را داریم:
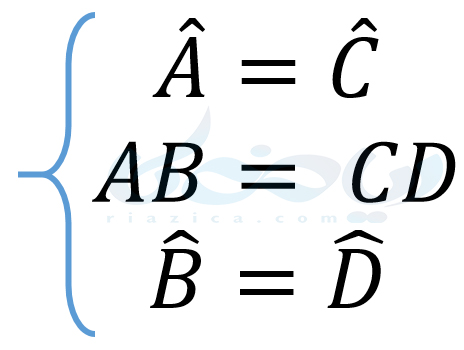
بنابراین \(\Large AB=CD\). به مثال بعدی از درسنامۀ حل مسئله در هندسه نهم توجه کنید.
برابری وترهای یک دایره
مثال 2: در شکل زیر وترهای \(\Large AB\) و \(\Large CD\) با هم برابرند. ثابت کنید کمانهای \(\Large AB\) و \(\Large CD\) نیز با یکدیگر برابرند.

حل: در گام اول، صورت مسئله را میخوانیم. در این مسئله نیز مانند مسئلۀ قبل با مفاهیمی مثل دایره، وتر، برابری وترهای دایره و برابری کمانهای دایره سر و کار داریم. در گام دوم، شکل مسئله را مانند مثال قبل تکمیل میکنیم. از آنجایی که می خواهیم با اثبات هم نهشتی مثلثهای \(\Large OAB\) و \(\Large OCD\)، برابری زوایای متناظر با کمانهای \(\Large AB\) و \(\Large CD\) را اثبات کنیم، خطوط اضافۀ زیر را که با خط چین مشخص شده است رسم میکنیم:

در گام سوم حل مسئله در هندسه نهم ، فرض و حکم مسئله را مشخص میکنیم. فرض مسئله این است که وترهای \(\Large AB\) و \(\Large CD\) با هم برابرند. خواستۀ مسئله که همان حکم مسئله است، اثبات برابری کمانهای \(\Large AB\) و \(\Large CD\) است. فرض و حکم را در جدولی به شکل زیر نشان میدهیم:

در گام چهارم، راه حل مناسب برای رسیدن از فرض به حکم را پیدا میکنیم. همانطور که گفتیم، از اثبات هم نهشتی مثلثهای \(\Large OAB\) و \(\Large OCD\)، برابری زوایای متناظر با کمانهای \(\Large AB\) و \(\Large CD\) و درنتیجه برابری خود این کمانها را اثبات میکنیم. برای اثبات همنهشتی مثلثهای \(\Large OAB\) و \(\Large OCD\) به صورت زیر عمل میکنیم:
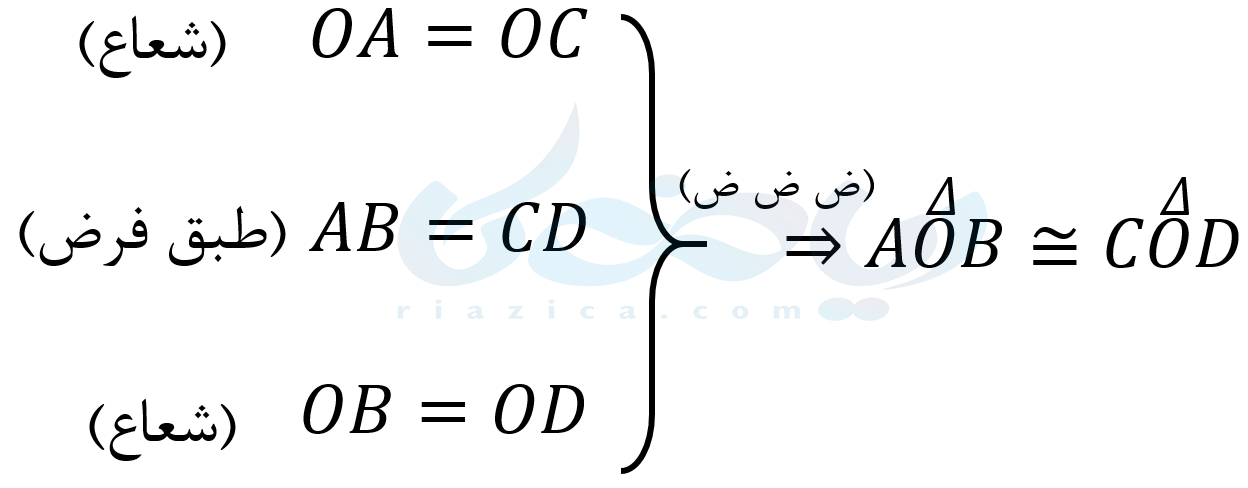
با توجه به این همنهشتی، تساویهای زیر را داریم:
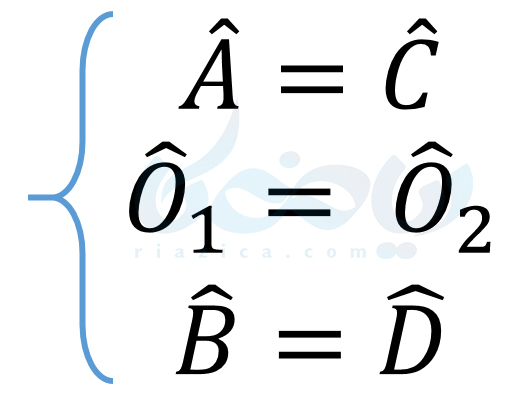
در نتیجه، باتوجه به برابری زوایای \(\Large O_1\) و \(\Large O_2\)، نتیجه میگیریم کمانهای \(\Large AB\) و \(\Large CD\) نیز با یکدیگر برابرند. به مثال بعدی از درسنامۀ حل مسئله در هندسه نهم توجه کنید.
نیمساز زاویۀ رأس
مثال 3: ثابت کنید فاصلۀ هر نقطه روی نیمساز زاویۀ رأس مثلث متساویالساقین، از دو سر قاعده برابر است.
حل: در گام اول، صورت مسئله را میخوانیم. در این مسئله با مفاهیمی مثل مثلث متساویالساقین، نیمساز، قاعده و فاصله از دو سر قاعده سر و کار داریم. در گام دوم، شکل مناسبی برای مسئله رسم میکنیم. بر خلاف دو مثال قبل، در این مثال شکلی به ما داده نشده. بنابراین اهمیت گام دوم در این مثال بیشتر از مثالهای قبلی است. شکل زیر را رسم میکنیم:
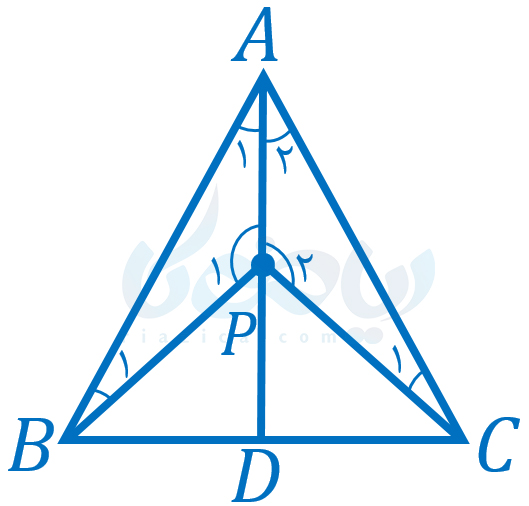
مثلث \(\Large ABC\) در شکل بالا متساویالساقین است. \(\Large AD\) نیمساز زاویۀ رأس مثلث، یعنی زاویۀ \(\Large A\) است. \(\Large P\) نقطۀ دلخواهی روی \(\Large AD\) است. در گام سوم حل مسئله در هندسه نهم ، فرض و حکم مسئله را مشخص میکنیم:
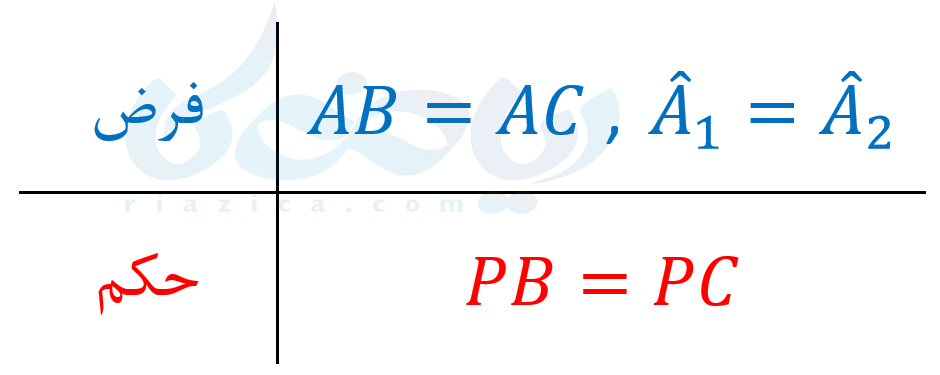
در گام چهارم، راه حل مناسب برای رسیدن از فرض به حکم را پیدا میکنیم. برای اثبات برابری \(\Large PB\) و \(\Large PC\) میتوانیم از هم نهشتی دو مثلث \(\Large APB\) و \(\Large APC\) استفاده کنیم:

در نتیجۀ این همنهشتی، تساویهای زیر را داریم:
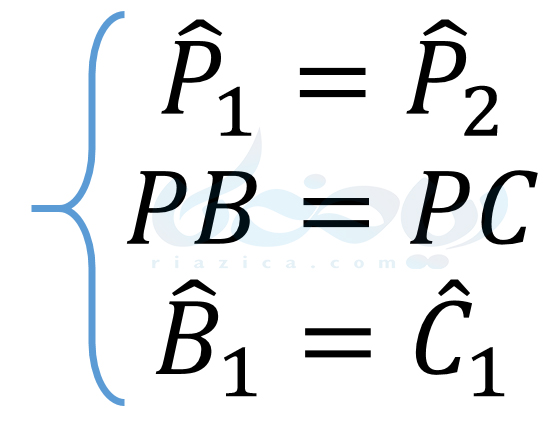
بنابراین \(\Large PB=PC\). یعنی فاصلۀ هر نقطۀ دلخواه روی \(\Large AD\) از \(\Large B\) و \(\Large C\) برابر است. به مثال بعدی از درسنامۀ حل مسئله در هندسه نهم توجه کنید.
مثال از متوازیالاضلاع
مثال 4: در شکل زیر، \(\Large ABCM\) و \(\Large ABMD\) متوازیالاضلاع هستند. ثابت کنید نقطۀ \(\Large M\) وسط \(\Large CD\) است.
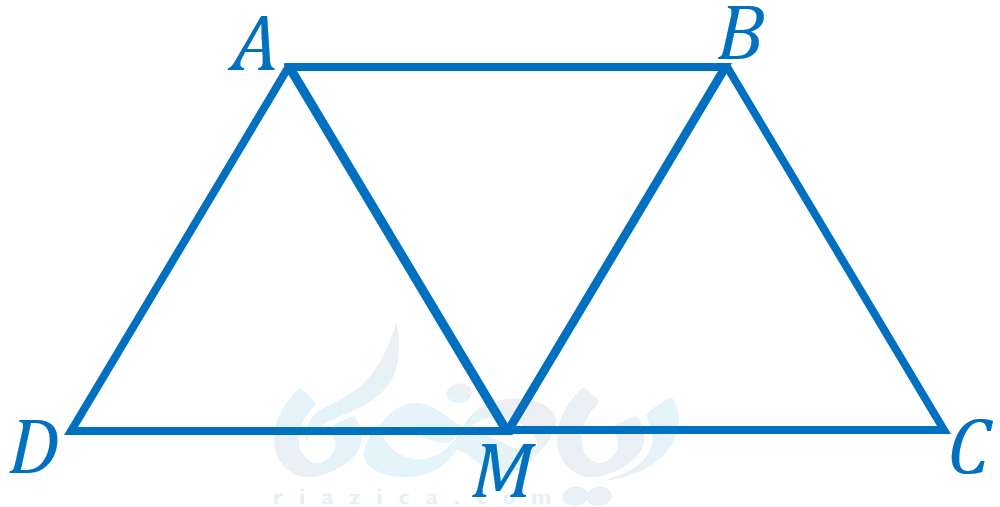
حل: در گام اول، صورت مسئله را میخوانیم. در این مسئله با مفاهیم مربوط به متوازیالاضلاع سر و کار داریم. در گام دوم، باید شکلی مناسب برای مسئله رسم کنیم. از آنجایی که خود مسئله شکل را به ما داده است، تنها برخی از زوایا را نام گذاری میکنیم:
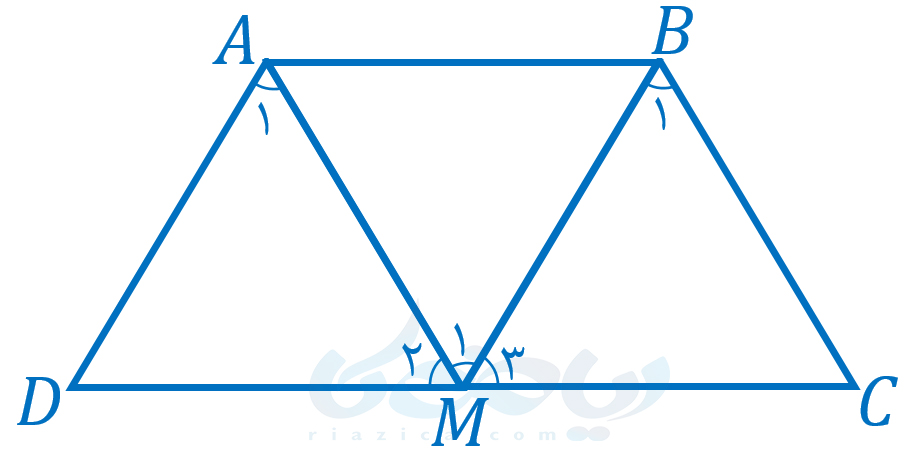
در گام سوم حل مسئله در هندسه نهم ، فرض و حکم مسئله را مشخص میکنیم:
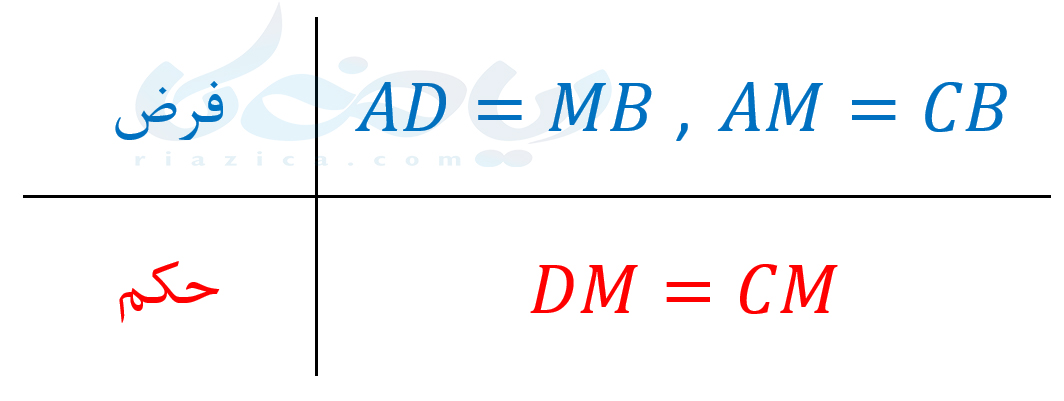
در گام چهارم، راه حل مناسب برای رسیدن از فرض به حکم را پیدا میکنیم. برای اثبات برابری \(\Large CM\) و \(\Large DM\) میتوانیم از هم نهشتی دو مثلث \(\Large BCM\) و \(\Large ADM\) استفاده کنیم:
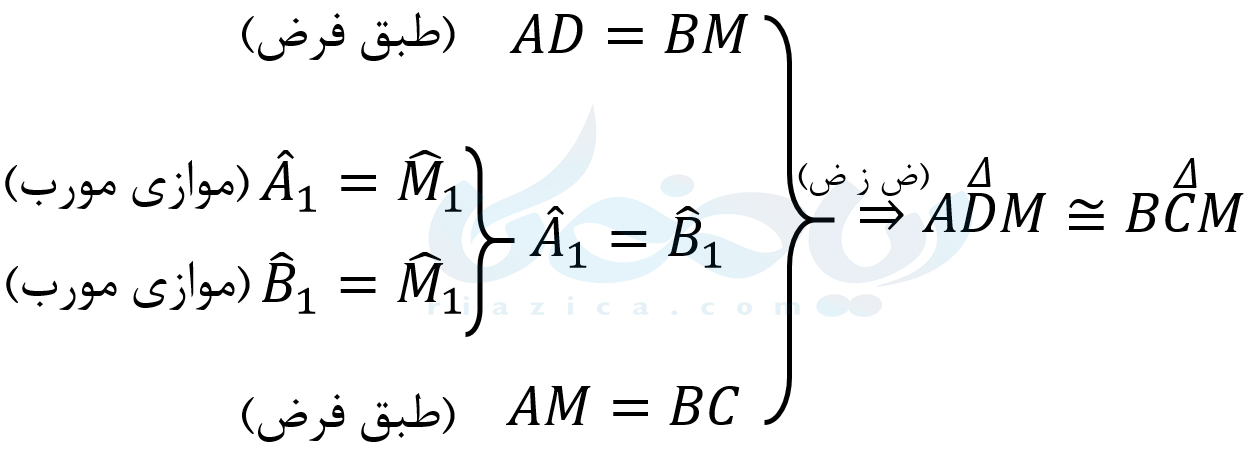
در نتیجۀ این همنهشتی، تساویهای زیر را داریم:
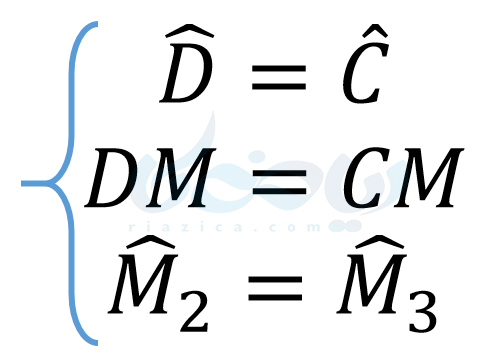
بنابراین \(\Large CM=DM\)، یعنی نقطۀ \(\Large M\) وسط \(\Large CD\) است.
زنگ آخر کلاس حل مسئله در هندسه نهم
به پایان این درسنامه از ریاضی نهم رسیدیم! چهار گام کلی (مطابق با کتاب درسی) برای حل مسئله هندسه نهم تعریف کردیم. همچنین، تعدادی مثال مختلف حل کردیم تا رعایت از این چهار گام را در حل مسئله نیز مشاهده کنید.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث حل مسئله در هندسه نهم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





عالی بود مرسی از سید امین موسوی نطنزی (:
ممنون از توضیحاتتون وراهنمایتون یه دنیا تشکر(✿
با سلام وادب
خواهش میکنم دوست عزیز
عااااالی
مرسی ممنون
با سلام وادب
ممنون از نظر لطف شما
خیلی خوب توضیح دادید ممنون از ریاضیکا
با سلام دوست عزیز
ممنون از لطف شما
عالی بود❣️
میشه بازم از این همنهشتی ها بزارین🌹
با سلام
ممنون دوست عزیز مبجث همنهشتی ها رو در پستهای دیگه کامل توضیح دادیم نمونه سوال وویدیو گذاشتیم