آموزش ریاضی پایه دوازدهم تجربی
بهینه سازی ریاضی دوازدهم تجربی 〽️📙 – یادگیری از طریق حل مثال
در درسنامهی پیش رو، به مبحث بهینه سازی ریاضی دوازدهم تجربی خواهیم پرداخت. در بهینه سازی ریاضی دوازدهم تجربی با مسائلی سروکار داریم که به دنبال کمترین یا بیشترین مقدار برای یک کمیت هستیم. این کمیت میتواند مساحت یک شکل باشد، یا هرینهی ساخت یک جسم و یا هر کمیت دلخواه دیگر.
برای حل مسائل بهینه سازی ریاضی دوازدهم تجربی ، نیازی به حفظ هیچ رابطه و فرمول اضافهای نیست. تنها باید از دانش قبلی خود در ریاضی استفاده کنیم. در ادامه با حل مثالهای بسیار مهم از این مبحث، کاملا به آن مسلط خواهیمشد.
مستطیل با بیشترین مساحت
مثال 1: در بین تمام مستطیلهای با محیط ثابت، عرض و طول مستطیلی را بیابید که بیشترین مساحت را دارد.
حل: طول مستطیل را \(\Large x \) و عرض آن را \(\Large y \) مینامیم. مساحت مستطیل برابر است با \(\Large S \). از طرفی محیط آن برابر با 8 است. پس

\(\LARGE 2(x+y)=8 \)
\(\LARGE x+y=4 \)
\(\LARGE \Rightarrow y=4-x \)
مساحت مستطیل را با استفاده از عبارت بالا بازنویسی میکنیم. یعنی داریم:
\(\begin{aligned} \LARGE S&\LARGE=xy \\&\LARGE=x(4-x)\\&\LARGE=4x-x^2\end{aligned}\)
رابطه ای که برای \(\Large S \) به دست آوردیم بدین معناست که اگر طول یک مستطیل با محیط 8، \(\Large x \) باشد، مساحت آن از رابطهی \(\Large S=4x-x^2 \) به دست میآید. برای اینکه ببینیم مستطیلهای دارای این ویژگی، یعنی با محیط 8، به ازای طول های مختلف چه مساحتی دارند، نمودار \(\Large S \) بر حسب \(\Large x \) را رسم میکنیم:

باید دقت کنیم، \(\Large x \) تنها میتواند بین 0 و 4 باشد. زیرا مجموع \(\Large x \) و \(\Large y \) برابر با 4 است. در غیر این صورت، مقدار یکی از اضلاع منفی میشود که غیر قابل قبول است. برای محاسبهی مینیمم تابع \(\Large S \) کافی است نقطهی بحرانی آن را پیدا کرده و مقدار تابع را در آن نقطه به دست آوریم. برای محاسبهی نقطهی بحرانی داریم:
\(\LARGE S'(x)=4-2x=0\)
\(\LARGE \Rightarrow x=2\)
حال که نقطهی بحرانی را به دست آوردیم، تابع مشتق را تعیین علامت میکنیم. با چگونگی تعیین علامت یک تابع، در درسنامهی تعیین علامت عبارتهای جبری آشنا شدهاید. جدول تغییرات تابع \(\Large S \) به صورت زیر در میآید:
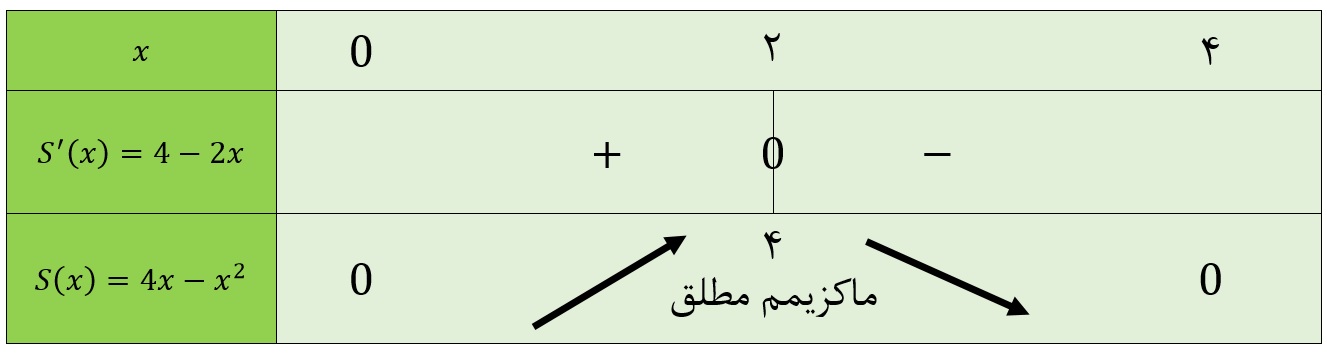
همانطور که از نمودار و جدول به روشنی پیداست، بیشترین مقدار مساحت زمانی حاصل میشود که \(\Large x \) برابر با 2 باشد. دقت کنید، \(\Large x=2 \) طول راس سهمی است که با نحوهی به دست آوردن آن را در سال یازدهم آشنا شدهاید. از آنجاییکه مجموع \(\Large x \) و \(\Large y \) برابر با 4 است، مقدار \(\Large y \) نیز برابر با 2 است. پس در واقع بیشترین مساحت، زمانی به دست میآید که مربعی به ضلع 2 داشتهباشیم.
کمترین حاصل ضرب در بهینه سازی ریاضی دوازدهم تجربی
مثال 2: دو عدد حقیقی بیابید که تفاضل آنها 5 باشد و حاصلضرب آنها کمترین مقدار ممکن گردد.
حل: یکی از اعداد را \(\Large x \) و دیگری را \(\Large y \) مینامیم. فرض میکنیم \(\Large x \) از \(\Large y \) بزرگتر است ( تفاوتی ندارد کدام یک را بزرگتر بگیرید. میتوانید \(\Large y \) را بزگتر از \(\Large x \) در نظر بگیرید. در این صورت باید جای \(\Large x \) و \(\Large y \) را در تمامی روابط پایین عوض کنید). داریم:
\(\LARGE x-y=5 \)
\(\LARGE \Rightarrow y=x-5 \)
\(\LARGE xy=x(x-5) \)
\(\LARGE xy=x^2-5x \)
حاصلضرب \(\Large xy \) را \(\Large M \) مینامیم. برای حل سوال، نیازی به رسم نمودار \(\Large M \) نیست. با این حال برای اینکه دید بهتری پیدا کنید، میتوانید نمودار را رسم کنید. نمودار \(\Large M \) بر حسب \(\Large x \) به صورت زیر در میآید:

برای محاسبهی مینیمم تابع \(\Large M \) کافی است نقطهی بحرانی آن را پیدا کرده و مقدار تابع را در آن نقطه به دست آوریم. برای محاسبهی نقطهی بحرانی داریم:
\(\LARGE M'(x)=2x-5=0\)
\(\LARGE \Rightarrow x=\frac{5}{2}\)
جدول تغییرات تابع \(\Large M \) به صورت زیر در میآید:

همان طور که در نمودار دیدید و در جدول تغییرات مشخص است، در \(\Large x=\frac{5}{2} \)، تابع مینیمم میشود. در اینجا نیز اکسترمم در راس سهمی قرار دارد. برای محاسبهی مقدار تابع در \(\Large x=\frac{5}{2} \) که کمترین حاصلضرب را به ما میدهد، روابط زیر را مینویسیم:
\(\LARGE y=x-5\)
\(\LARGE \Rightarrow y=\frac{5}{2}-5=-\frac{5}{2}\)
\(\LARGE \Rightarrow xy=(\frac{5}{2}) \times (-\frac{5}{2}) \)
\(\LARGE \Rightarrow xy=-\frac{25}{4}\)
گامهای اساسی در حل مسائل بهینه سازی ریاضی دوازدهم تجربی
همان طور که در مثال 1 و 2 دیدید، برای حل مسائل بهینه سازی ریاضی دوازدهم تجربی، سه گام مهم وجود دارد.
- گام اول، پیدا کردن تابع تغییرات کمیت است.
- گام دوم، پیدا کردن نقطهی بحرانی تابع است.
- گام سوم، محاسبهی اکسترمم تابع با توجه به نقطهی بحرانی است.
- در ادامه، چند مثال کمی پیشرفته تر از بهینه سازی ریاضی دوازدهم تجربی با یکدیگر خواهیمدید.
یک مثال جذاب از بهینه سازی ریاضی دوازدهم تجربی
مثال 3: میخواهیم کنار یک رودخانه، محوطهای را به شکل مثلث متساوی الساقین نردهکشی کنیم. قاعدهی مثلث منطبق بر رودخانه است. اگر 20 متر نرده داشته باشیم، بیشترین مساحت ممکن برای این مثلث چهقدر است؟
حل: به شکل زیر نگاه کنید. قاعدهی مثلث بر رودخانه منطبق است. پس در قاعده نیازی به نرده نداریم. مجموع طول نرده برای دو ساق، 10 متر است. مطابق شکل، ارتفاع مثلث را \(\Large h \) و نصف قاعدهی مثلث را \(\Large a \) مینامیم.

مساحت مثلث که با \(\Large S \) نشان میدهیم برابر است با:
\(\LARGE S=\frac{2a \times h}{2}=ah\)
\(\LARGE h=\sqrt{10^2-a^2}\)
\(\LARGE S=a\sqrt{10^2-a^2}\)
رسم نمودار \(\Large S \) کمی دشوار است. نیازی هم به رسم نمودار نیست. در صورتی که نقطهی بحرانی را به دست آورده و جدول تغییرات \(\Large S \) را رسم کنیم، ماکزیمم \(\Large S \) قابل محاسبه خواهد بود. با این حال برای اینکه دید بهتری پیدا کنید، نمودار \(\Large S \) بر حسب \(\Large x \) را در زیر رسم میکنیم:

\(\begin{aligned} \LARGE S’&\LARGE=\sqrt{10^2-a^2}\\&\LARGE+\frac{-a}{\sqrt{10^2-a^2}} \times a \end{aligned}\)
\(\LARGE S’=\frac{10^2-2a^2}{\sqrt{10^2-a^2}}=0\)
\(\LARGE \Rightarrow a^2=50\)
\(\LARGE \Rightarrow a=\sqrt{50}\)
جدول تغییرات تابع \(\Large S \) نیز به صورت زیر است:
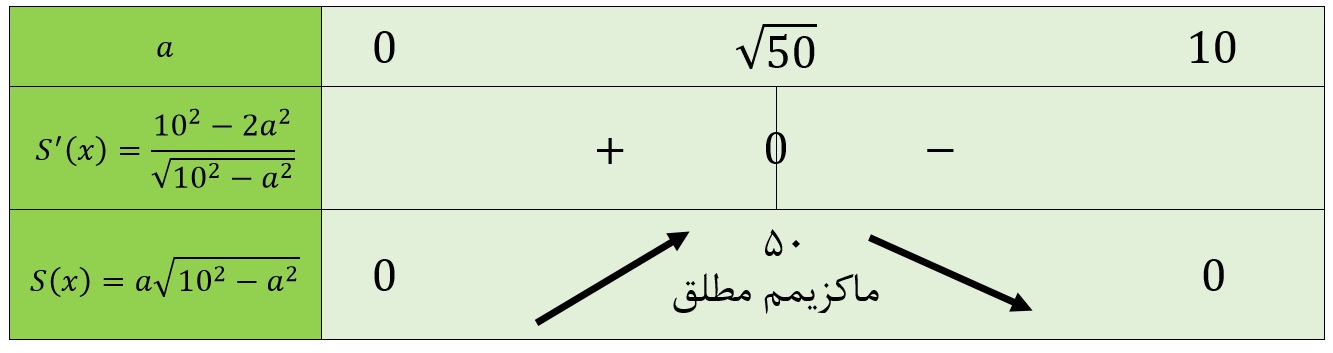
با توجه به نقطهی بحرانی و جدول تغییرات، بیشترین مساحت مثلث زمانی حاصل میشود که \(\Large a=\sqrt{50} \) باشد. در نتیجه \(\Large h = \sqrt{10^2-a^2} \) که در نهایت حاصل \(\Large h = \sqrt{50} \) خواهد شد. در این حالت مساحت ماکزیمم برابر خواهد بود با:
\(\begin{aligned} \LARGE S&\LARGE=ah\\&\LARGE=\sqrt{50} \times \sqrt{50}=50 \end{aligned}\)
مساحت مسطیل بین سهمی و محور مختصات
مثال 4: بیشترین مساحت ممکن برای مستطیلی که دو راس آن روی محور \(\Large x \)ها و دو راس دیگرش بالای محور \(\Large x \)ها و روی سهمی به معادلهی \(\Large y=48-4x^2 \) باشد را پیدا کنید.
حل: به شکل زیر نگاه کنید. یک مستطیل با شرایطی که در مساله گفته شده رسم شده است. طول مستطیل \(\Large 2x \) و عرض آن \(\Large 48-4x^2 \) است.

اگر مساحت مستطیل را با \(\Large S \) نشان دهیم، مقدار آن از رابطهی زیر به دست میآید:
\(\LARGE S=2x(48-4x^2)\)
\(\LARGE \Rightarrow S=96x-8x^3\)
نیازی به رسم نمودار \(\Large S \) بر حسب \(\Large x \) نیست. کافی است نقطهی بحرانی را به دست آوریم. سپس با استفاده از جدول تغییرات \(\Large S \)، ماکزیمم مساحت را محاسبه خواهیمکرد. برای محاسبهی نقطهی بحرانی داریم:
\(\LARGE S’=96-24x^2\)
\(\LARGE S’=0 \Rightarrow x^2=4\)
\(\LARGE \Rightarrow x=2, -2\)
\(\Large x \) مثبت است، چون طول ضلع مستطیل نمیتواند منفی باشد. در نتیجه \(\Large x=2 \) نقطهی بحرانی مورد نظر ماست. جدول تغییرات تابع \(\Large S \) به صورت زیر است:
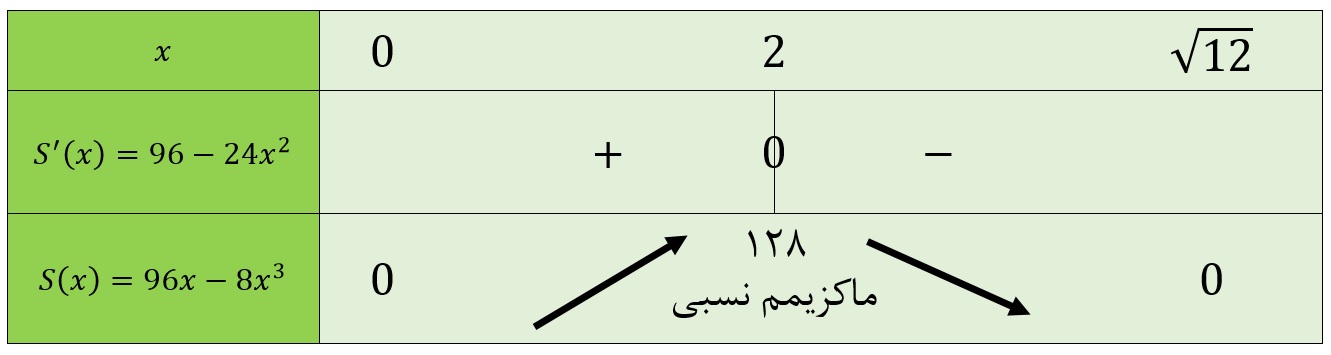
پس ماکزیمم مساحت مستطیل، زمانی به دست می آید که \(\Large x=2 \) باشد. مقدار \(\Large S \) به ازای \(\Large x=2 \) برابر خواهد بود با:
\(\LARGE S=2x \times (48-4x^2)\)
\(\begin{aligned} \LARGE \Rightarrow S&\LARGE=4\times(48-16)\\&\LARGE=4 \times 32=128 \end{aligned}\)
قبل از خونون ین پست حتما پستهای اکسترمم نسبی ویکنوایی ونقطه بحرانی ریاضی دوازدهم واکسترمم مطلق را بخوانید.
زنگ آخر کلاس بهینه سازی ریاضی دوازدهم تجربی
همان طور که گفتیم، برای حل مسائل بهینه سازی ریاضی دوازدهم تجربی باید سه گام اساسی را درست برداریم.
- گام اول یافتن تابع تغییرات کمیتی است که با آن سر و کار داریم. در این گام باید نسبت به تعیین دامنهی تابع دقت کنیم.
- گام دوم، پیدا کردن نقاط بحرانی تابعی است که در گام اول یافتیم.
- گام سوم، پیدا کردن اکسترمم تابع است. بسته به خواستهی مساله، گاهی این اکسترمم ماکزیمم است و گاهی مینیمم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث بهینه سازی ریاضی دوازدهم تجربی دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.




