آموزش ریاضی پایه نهم
توان صحیح ریاضی نهم ✅*️⃣ – صحیح یادش بگیر!
در درسنامۀ توان صحیح ریاضی نهم توانهای صحیح را معرفی کرده و روابط مربوط به آنها را بررسی میکنیم. با توانهای طبیعی در سال گذشته آشنا شدهاید. بنابراین نکتۀ جدید این مبحث، توانهای منفی و نحوۀ محاسبۀ آنهاست. پیشنهاد میکنیم در صورتی که توانهای طبیعی را فراموش کردهاید، قبل از مطالعۀ این درسنامه، درسنامۀ ضرب و تقسیم اعداد تواندار را مرور کنید. به قسمت اول از درسنامۀ توان صحیح ریاضی نهم توجه کنید.
توان منفی
نمیتوانیم در مورد توانهای منفی، مانند توانهای مثبت صحبت کنیم. مثلاً وقتی مینویسیم \(\Large 2^3\)، در توضیح آن میتوانیم بگوییم که باید \(\Large 2\) را \(\Large 3\) بار در خودش ضرب کنیم. اما به طور مثال اگر داشته باشیم \(\Large 2^{-3}\) نمیتوانیم بگوییم \(\Large 2\) را \(\Large -3\) بار در خودش ضرب کنیم. زیرا شهودی نسبت به ضرب به تعداد منفی نداریم. بنابراین باید توان منفی را تعریف کنیم.
تعریف: اگر \(\Large m\) عددی طبیعی و \(\Large a\) عددی غیر صفر باشد، آنگاه توان منفی را به صورت زیر تعریف میکنیم:
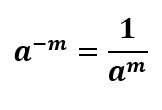
بنابراین به زبان ساده، برای به دست آوردن توان منفی یک عدد کافی است پایه را معکوس کرده و به توان مثبت برسانیم. به مثالهای زیر از درسنامۀ توان صحیح ریاضی نهم توجه کنید.
مثال از توان منفی
مثال 1: حاصل \(\Large 2^{-3}\) را به صورت یک کسر بنویسید.
حل: با توجه به تعریف توان منفی داریم:
\(\LARGE 2^{-3}=\frac{1}{2^3}=\frac{1}{8}\)
به مثال بعدی از درسنامۀ توان صحیح ریاضی نهم توجه کنید.
مثال از توان منفی یک کسر
مثال 2: عبارت \(\Large (\frac{3}{5})^{-2}\) را ساده کنید.
حل: تفاوتی نمیکند که یک کسر توان منفی داشته باشد، یا یک عدد صحیح توان منفی داشته باشد. در هر صورت از تعریف استفاده میکنیم:
\(\LARGE (\frac{3}{5})^{-2}=\frac{1}{(\frac{3}{5})^{2}}=\frac{1}{\frac{9}{25}}=\frac{25}{9}\)
میتوانیم جواب را که همان کسر \(\Large \frac{25}{9}\) است، به صورت \(\Large (\frac{5}{3})^2\) نیز بنویسیم. به طور کلی اگر \(\Large m\) عددی طبیعی و \(\Large a\) عددی غیر صفر باشد، آنگاه داریم:
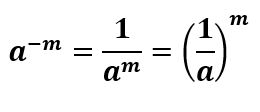
به مثال بعدی از درسنامۀ توان صحیح ریاضی نهم توجه کنید.
مثال از توان منفی یک عدد منفی
مثال 3: حاصل \(\Large (\frac{3}{4})^{-3}\) را به صورت یک عدد تواندار با توان طبیعی بنویسید.
حل: با توجه به تعریف داریم:
\(\LARGE (\frac{3}{4})^{-3}=\frac{1}{(\frac{3}{4})^{3}}\)
\(\LARGE =\frac{1}{\frac{27}{64}}\)
\(\LARGE =\frac{64}{27}\)
\(\LARGE =(\frac{4}{3})^3\)
به قسمت بعدی از درسنامۀ توان صحیح ریاضی نهم توجه کنید.
ضرب و تقسیم اعداد با توان صحیح
در پایۀ هشتم و در درسنامۀ ضرب و تقسیم اعداد تواندار، قواعد ساده سازی ضرب و تقسیم اعداد تواندار با توان طبیعی را مطالعه کردهاید. تمام آن قوانین، برای توانهای صحیح نیز برقرار است. برای اینکه به طور منسجم و با ذکر مثال، این روابط را برای توانهای صحیح نیز بیان کنیم، هر رابطه را در یک بخش جداگانه توضیح میدهیم و در انتها همۀ آنها در یک جدول میبینیم.
رابطۀ اول در توان صحیح ریاضی نهم
اگر \(\Large m\) و \(\Large n\) دو عدد صحیح باشند و \(\Large a\) یک عدد غیر صفر، آنگاه داریم:
\(\LARGE a^m\times a^n=a^{m+n}\)
به مثال بعدی از درسنامۀ توان صحیح ریاضی نهم توجه کنید.
مثال از رابطۀ اول
مثال 4: حاصل \(\Large 3^{2}\times 3^{-6}\) را به دست آورید.
حل: با توجه به رابطۀ اول داریم:
\(\LARGE 3^{2}\times 3^{-6}=3^{2-6}\)
\(\LARGE =3^{-4}\)
\(\LARGE =\frac{1}{3^4}\)
مثال 5: حاصل \(\Large (\frac{xy}{z})^{3}\times (\frac{xy}{z})^{-4}\) را به دست آورید.
حل: با توجه به رابطۀ اول داریم:
\(\LARGE (\frac{xy}{z})^{3}\times (\frac{xy}{z})^{-4}=(\frac{xy}{z})^{3-4}\)
\(\LARGE =(\frac{xy}{z})^{-1}\)
\(\LARGE =\frac{z}{xy}\)
در قسمت بعدی از درسنامۀ توان صحیح ریاضی نهم رابطۀ دوم را بیان میکنیم.
رابطۀ دوم در توان صحیح ریاضی نهم
اگر \(\Large m\) و \(\Large n\) دو عدد صحیح و \(\Large a\) یک عدد غیر صفر باشد، آنگاه داریم:
\(\LARGE \frac{a^m}{a^n}=a^m \div a^n=a^{m-n}\)
مثال از رابطۀ دوم
مثال 6: حاصل \(\Large \frac{2^4}{2^5}\) را به دست آورید.
حل: با توجه به رابطۀ دوم داریم:
\(\LARGE \frac{2^4}{2^5}=2^{4-5}=2^{-1}=\frac{1}{2}\)
به مثال بعدی از درسنامۀ توان صحیح ریاضی نهم توجه کنید.
مثال 7: حاصل \(\Large \frac{3^4 \times 5^7}{3^6 \times 5^2}\) را به دست آورید.
حل: ابتدا عبارت داده شده را ساده کرده و سپس از رابطۀ دوم استفاده میکنیم:
\(\LARGE \frac{3^4 \times 5^7}{3^6 \times 5^2}=\frac{3^4}{3^6} \times \frac{5^7}{5^2}\)
\(\LARGE =3^{4-6} \times 5^{7-2}\)
\(\LARGE =3^{-2} \times 5^{5}\)
\(\LARGE =\frac{5^{5}}{3^{2}} \)
در قسمت بعدی از درسنامۀ توان صحیح ریاضی نهم رابطۀ سوم را بیان میکنیم.
رابطۀ سوم در توان صحیح ریاضی نهم
اگر \(\Large m\) یک عدد صحیح و \(\Large a\) و \(\Large b\) دو عدد دلخواه و مخالف صفر باشند، آنگاه داریم:
\(\LARGE \frac{a^m}{b^m}=(\frac{a}{b})^m\)
مثال از رابطۀ سوم
مثال 8: حاصل \(\Large (\frac{-7}{12})^{-2} \times 36^{-2}\) را به دست آورید.
حل: به روشهای مختلفی میتوان عبارت داده شده را ساده کرد. برای اینکه از رابطۀ سوم استفاده کرده باشیم، به صورت زیر عمل میکنیم:
\(\LARGE (\frac{-7}{12})^{-2} \times 36^{-2}\)
\(\LARGE =\frac{(-7)^{-2}}{12^{-2}}\times 36^{-2}\)
\(\LARGE =(-7)^{-2}\times (\frac{36}{12})^{-2} \)
\(\LARGE =(-7)^{-2}\times 3^{-2} \)
\(\LARGE =(-21)^{-2} \)
\(\LARGE =\frac{1}{21^2}\)
در قسمت بعدی از درسنامۀ توان صحیح ریاضی نهم رابطۀ چهارم را بیان میکنیم.
رابطۀ چهارم در توان صحیح ریاضی نهم
اگر \(\Large m\) یک عدد صحیح و \(\Large a\) و \(\Large b\) دو عدد دلخواه باشند، آنگاه داریم:
\(\LARGE (ab)^m=a^m \times b^m\)
مثال از رابطۀ چهارم
مثال 9: حاصل \(\Large \frac{6^3}{2^4}\) را به دست آورید.
حل: ابتدا عبارت را ساده کرده و سپس از رابطۀ چهارم استفاده میکنیم:
\(\LARGE \frac{6^3}{2^4}=\frac{(2 \times 3)^3}{2^4}\)
\(\LARGE =\frac{2^3 \times 3^3}{2^4}\)
\(\LARGE =\frac{2^3}{2^4} \times 3^3\)
\(\LARGE =2^{-1} \times 3^3\)
\(\LARGE =\frac{3^3}{2} \)
در قسمت بعدی از درسنامۀ توان صحیح ریاضی نهم رابطۀ پنجم را بیان میکنیم.
رابطۀ پنجم در توان صحیح ریاضی نهم
اگر \(\Large m\) و \(\Large n\) دو عدد صحیح و \(\Large a\) یک عدد دلخواه باشد، آنگاه داریم:
\(\LARGE (a^m)^n=a^{mn}\)
مثال از رابطۀ پنجم
مثال 10: حاصل \(\Large ((-\frac{3}{5})^{-3})^{-2}\) را به دست آورید.
حل: با توجه به رابطۀ پنجم داریم:
\(\LARGE ((-\frac{3}{5})^{-3})^{-2}\)
\(\LARGE =(-\frac{3}{5})^{(-3) \times (-2)}\)
\(\LARGE =(-\frac{3}{5})^{6}\)
\(\LARGE =\frac{3^6}{5^6}\)
در قسمت بعدی از درسنامۀ توان صحیح روابطی که تا اینجا فراگرفتهایم، مرور میکنیم.
جمع بندی روابط
برای اینکه تمامی روابط را یکجا داشته باشیم، در جدول زیر همۀ آنها را آوردهایم:

دقت کنید که در روابط بالا، \(\Large m\) و \(\Large n\) اعداد صحیح و \(\Large a\) و \(\Large b\) اعداد غیر صفر هستند.
زنگ آخر کلاس توان صحیح
به پایان این درسنامه از ریاضی نهم رسیدیم. مبحث جدیدی که در این درسنامه فرا گرفتیم، توانهای منفی بود. همانطور که دیدید، میتوانیم از روابطی که برای توانهای طبیعی برقرار بود، برای توانهای منفی نیز استفاده کنیم. حل مثالهای متنوع این درسنامه، کمک زیادی به درک بهتر این مبحث خواهد کرد.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث توان صحیح ریاضی نهم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





بهترینسایته
با سلام وادب ممنون از لطف شما