آموزش ریاضی پایه دوازدهم تجربی
حد بی نهایت ♾💬 – زیباتر از تصور!
در این درسنامه به حد بی نهایت میپردازیم. حد بینهایت چیست؟ تفاوت حد بی نهایت با حد در بی نهایت چیست؟ چه حدهایی بینهایت یا اصطلاحا نا متناهی میشوند؟ ابتدا چند مبحث را مرور کرده و سپس به این سوالات پاسخ میدهیم.
تقسیم و بخش پذیری چند جمله ای ها
با تقسیم چند جمله ای ها در پایۀ نهم آشنا شدید. در مبحث حد بی نهایت به طور جدی نیاز به تسلط بر تقسیم و بخش پذیری چند جمه ای ها داریم. ابتدا برای یادآوری، یک مثال از این مبحث حل خواهیم کرد. سپس، به بیان یک قضیه و اثبات آن خواهیم پرداخت.
مثال از تقسیم چند جمله ای ها
مثال 1: چند جمله ای \(\Large x^2+3x-3 \) را بر دو جمله ای \(\Large x-1 \) تقسیم کنید.
حل:
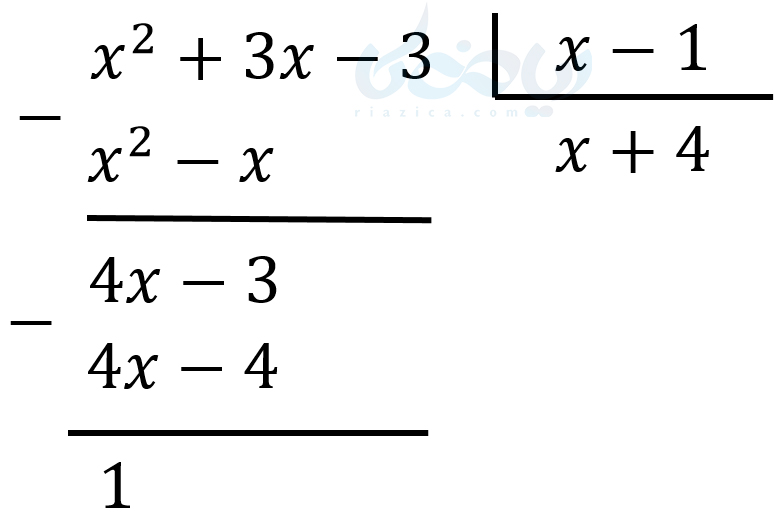
همان طور که میبینید، خارج قسمت تقسیم برابر شد با \(\Large x+4 \) و باقی ماندۀ آن برابر شد با 1. اما در چه شرایطی یک چند جمله ای بر یک دو جمله ای مثل \(\Large (x-a) \) بخش پذیر است؟ پاسخ به این سوال را با استفاده از قضیۀ زیر میدهیم. این قضیه در مفهوم حد بی نهایت بسیار استفاده خواهد شد.
قضیه: باقی ماندۀ تقسیم چند جمله ای \(\Large f(x) \) بر دو جمله ای \(\Large (x-a) \) برابر است با \(\Large f(a) \).
در نتیجۀ این قضیه، زمانی چند جمله ای \(\Large f(x) \) بر \(\Large (x-a) \) بخش پذیر است که \(\Large f(a) \) برابر با 0 باشد. اثبات این قضیه به سادگی انجام میشود. فرض کنید در تقسیم چند جمله ای \(\Large f(x) \) بر \(\Large (x-a) \)، خارج قسمت را با \(\Large Q(x) \) و باقی مانده را با \(\Large R \) نشان دهیم. در این صورت داریم:
\(\LARGE f(x)=(x-a)Q(x)+R \)
اگر در عبارت بالا \(\Large x \) را برابر با \(\Large a \) قرار دهیم، خواهیم داشت:
\(\LARGE f(a)=0+R \)
در نتیجه \(\Large R \) که همان باقی مانده است برابر است با \(\Large f(a) \). بنابراین برای محاسبۀ باقی ماندۀ تقسیم چند جمله ای \(\Large f(x) \) بر \(\Large (x-a) \)، نیازی به محاسبۀ تقسیم نیست. کافی است مقدار \(\Large f(a) \) را به دست آوریم. به طور مثال در مثال 1، بدون محاسبۀ تقسیم میتوان گفت باقی ماندۀ چند جملهای \(\Large x^2+3x-3 \) بر دو جمله ای \(\Large x-a \) برابر است با \(\Large f(1) \) که مقدار \(\Large f(1) \) نیز برابر با 1 است. از این مطلب برای تجزیۀ چند جمله ای ها نیز میتوان استفاده کرد. به مثال زیر دقت کنید.
مثال از تجزیۀ چند جمله ای ها
مثال 2: چند جمله ای \(\Large f(x)=x^3-2x^2-2x-3 \) را تجزیه کنید.
حل: با استفاده از قضیه ای که بیان کردیم، از آنجاییکه \(\Large f(3) \) برابر با 0 است، چند جمله ای\(\Large f(x) \) بر \(\Large (x-3) \) بخش پذیر است. در نتیجه، \(\Large f(x) \) را میتوان به صورت حاصل ضرب \(\Large (x-3) \) در یک عامل دیگر نوشت. اگر \(\Large f(x) \) را بر \(\Large (x-3) \) تقسیم کنیم، عامل دوم نیز به صورت زیر به دست میآید:
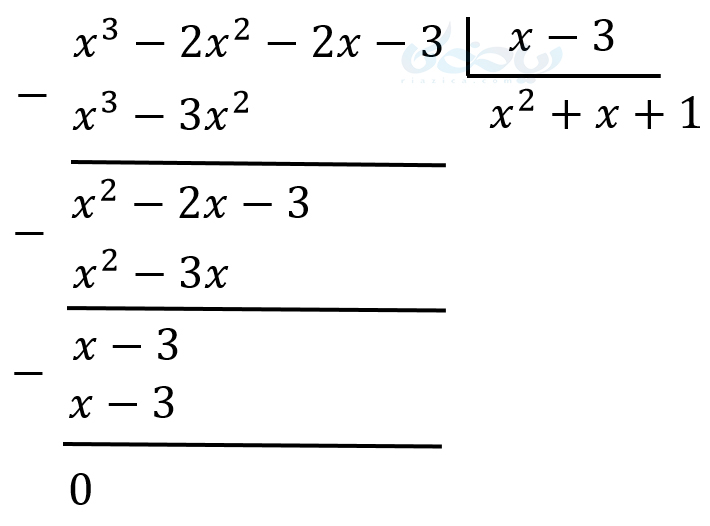
حد توابع کسری
یکی دیگر از مباحثی که برای معرفی حد بی نهایت کلیدی است، حد توابع کسری است. با محاسبۀ حد توابع کسری در سال یازدهم آشنا شدید. در صورتی که صورت و مخرج یک کسر به اعداد حقیقی میل کرده و حد مخرج مخالف صفر باشد، حد عبارت کسری برابر است با تقسیم حد صورت بر مخرج. برای یاد آوری، به مثال زیر دقت کنید.
مثال 3: حد \(\Large \lim\limits_{x\to 1} \frac{x^2+2x+3}{2x^3+1} \) را به دست آورید.
حل:
\(\LARGE \lim\limits_{x\to 1} \frac{x^2+2x+3}{2x^3+1} \)
\(\LARGE =\frac{1+2+3}{2+1}=2\)
همان طور که دیدید، حد عبارت کسری بالا به سادگی به دست آمد. اما مشکل جایی پیش میآید که صورت و مخرج هر دو به صفر میل کنند. در این صورت نیز برای برخی از حالات، حد وجود دارد. در ادامه دو حالت متداول را بررسی میکنیم.
تجزیۀ صورت و مخرج در محاسبۀ حد
در برخی از حالتها که صورت و مخرج یک کسر به صفر میل میکنند، با تجزیۀ صورت و مخرج و ساده کردن آنها میتوان حد را محاسبه کرد. در صورتی که تجزیۀ عبارتهای جبری را فراموش کردهاید، به درسنامۀ تجزیه عبارت های حبری به 4 روش مختلف مراجعه کنید.
مثال 4: حد \(\Large \lim\limits_{x\to -2} \frac{x^3+3x^2+5x+6}{x^2+5x+6} \) را به دست آورید.
حل:
\(\LARGE \lim\limits_{x\to -2} \frac{x^3+3x^2+5x+6}{x^2+5x+6} \)
\(\LARGE =\lim\limits_{x\to -2} \frac{(x+2)(x^2+x+3)}{(x+2)(x+3)} \)
\(\LARGE =\lim\limits_{x\to -2} \frac{x^2+x+3}{x+3} \)
\(\LARGE =5 \)
همان طور که دیدید، حد صورت و مخرج کسر به صفر میل میکرد. صورت و مخرج را تجزیه و عبارت \(\Large (x+2) \) را ساده کردیم. در نتیجه، مقدار حد به دست آمد. تجزیۀ مخرج ساده بود، اما از کجا حدس زدیم که صورت کسر باید این گونه تجزیه شود؟ همان طور که در ابتدای درسنامه دیدیم، از قضیهی بخش پذیری بر دو جمله ای ها برای تجزیۀ عبارات جبری نیز میتوان استفاده کرد. اگر صورت را \(\Large N(x) \) و مخرج را \(\Large D(x) \) بنامیم، از آنجاییکه \(\Large N(2)=0 \) و \(\Large D(2)=0 \)، هم صورت و هم مخرج بر دو جمله ای \(\Large (x+2) \) بخش پذیر هستند. در نتیجه میتوان پس ازتجزیۀ صورت و مخرج، عبارت \(\Large (x+2) \) را ساده کرد.
ضرب عبارات رادیکالی در صورت و مخرج
در برخی از عبارات کسری، در صورت یا مخرج کسر، یک عبارت رادیکالی وجود دارد. در برخی از حالات، با ضرب یک عبارت رادیکالی مناسب در صورت و مخرج کسر، یک عامل مشترک در صورت و مخرج به وجود میآید. از ساده کردن عامل مشترک میتوان در محاسبۀ حد عباراتی که صورت و مخرج آنها به صفر میل میکنند، استفاده کرد. در صورتی که چگونگی ضرب و تقسیم رادیکالها را فراموش کرده اید، به درسنامۀ خواص ضرب و تقسیم رادیکال ها ریاضی هشتم و پست گویا کردن مخرجهای گنگ مراجعه کنید. به مثال زیر توجه کنید.
مثال 5: حد \(\Large \lim\limits_{x\to 1} \frac{x-\sqrt{2x-1}}{x-1} \) را به دست آورید.
حل:
\(\LARGE \lim\limits_{x\to 1} \frac{x-\sqrt{2x-1}}{x-1} \)
\(\LARGE =\lim\limits_{x\to 1} \frac{x-\sqrt{2x-1}}{x-1} \times \frac{x+\sqrt{2x-1}}{x+\sqrt{2x-1}} \)
\(\LARGE =\lim\limits_{x\to 1} \frac{x^2-(2x-1)}{(x-1)(x+\sqrt{2x-1})} \)
\(\LARGE =\lim\limits_{x\to 1} \frac{(x-1)^2}{(x-1)(x+\sqrt{2x-1})} \)
\(\LARGE =\lim\limits_{x\to 1} \frac{x-1}{x+\sqrt{2x-1}} \)
\(\LARGE =0\)
حد نامتناهی
برای تعریف حد بی نهایت یا همان حد نا متناهی، هنوز لازم است تا یک مفهوم دیگر را معرفی کنیم. ابتدا همسایگی ، همسایگی محذوف و همسایگی راست و چپ را تعریف میکنیم. سپس به معرفی حد بینهایت خواهیم پرداخت. لازم به ذکر است که تمامی تعریفهای پایین در مجموعۀ اعداد حقیقی است.
همسایگی
در صورتی که \(\Large x_0 \in (a, b) \) باشد، بازۀ باز \(\Large (a, b) \) را یک همسایگی \(\Large x_0 \) مینامیم. به طور مثال، بازۀ \(\Large (1, 3) \)، یک همسایگی عدد حقیقی \(\Large 2 \) است.
همسایگی محذوف
مجموعۀ \(\Large (a, b)-{x_0} \) را یک همسایگی محذوف \(\Large x_0 \) مینامیم. در واقع اگر خود عدد را از یک همسایگی آن حذف کنیم، یک همسایگی محذوف آن عدد به دست میآید. یه طور مثال، مجموعۀ \(\Large (1, 3)-{2} \)، یک همسایگی محذوف عدد حقیقی \(\Large 2 \) است.
همسایگی راست و چپ
اگر \(\Large d \) عددی مثبت باشد، \(\Large (x_0, x_0+d) \) یک همسایگی راست \(\Large x_0 \) و \(\Large (x_0-d, x_0) \) یک همسایگی چپ \(\Large x_0 \) نام دارد. مثلا، \(\Large (2, 3) \)، یک همسایگی راست عدد حقیقی \(\Large 2 \) و \(\Large (1, 2) \) یک همسایگی چپ آن است.
آشنایی با حد بی نهایت (نامتناهی)
برای اینکه با مفهوم حد بینهایت آشنا شوید، فرض کنید می خواهیم حد تابع \(\Large f(x)=\frac{1}{|x|} \) را در نقطۀ \(\Large x=0 \) حساب کنیم. میدانیم \(\Large f(x) \) در \(\Large x=0 \) مقدار ندارد. پس سعی میکنیم تا طبق تعریف حد به نقطۀ \(\Large x=0 \) نزدیک شویم تا شاید بتوانیم حد تابع را در \(\Large x=0 \) به دست آوریم. در جدول زیر از راست و چپ به نقطۀ \(\Large x=0 \) نزدیک شدهایم.

همان طور که در جدول بالا میبینید، هر چه قدر به 0 نزدیک میشویم، مقدار \(\Large f(x) \) بزرگ میشود. در واقع اگر به اندازۀ کافی به 0 نزدیک شویم، مقدار \(\Large f(x) \) از هر مقدار دلخواهی بزرگتر خواهد شد. برای اینکه بهتر متوجه شوید، نمودار تابع \(\Large f(x) \) که در شکل زیر رسم شده است را در نظر بگیرید.
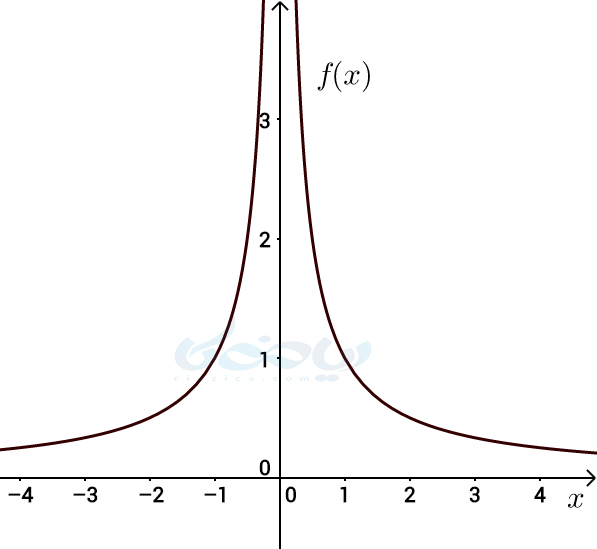
فرض کنید میخواهیم به مقادیر \(\Large f(x)>10^5 \) دست پیدا کنیم. در این صورت کافی است \(\Large x \) را از \(\Large \frac{1}{10^5} \) کوچکتر کرده و به 0 نزدیک شویم. در این صورت \(\Large f(x)=\frac{1}{|x|} \) از \(\Large 10^5 \) بزرگتر خواهد شد. برای هر عدد بزرگ دلخواهی میتوان این کار را انجام داد. در چنین شرایطی میگوییم حد \(\Large f(x) \) در \(\Large x=0 \) برابر با مثبت بی نهایت است و مینویسیم \(\Large \lim\limits_{x\to 0} f(x)=+\infty \). دقت کنید، همان طور که در درسنامۀ مشتق پذیری دوازدهم تجربی اشاره کردیم، \(\Large +\infty \) و \(\Large -\infty \) اعداد حقیقی نیستند. فقط به جهت توصیف چنین شرایطی از این نمادها استفاده میکنیم (به طور دقیقتر، \(\Large +\infty\) و \(\Large -\infty\) جزء دستگاه اعداد حقیقی توسیع یافته هستند که در این درس با آن ها سر و کار نداریم).
تعریف حد مثبت بی نهایت
در صورتی که \(\Large f(x)\) در یک همسایگی محذوف \(\Large a \) تعریف شده باشد، \(\Large \lim\limits_{x\to a} f(x)=+\infty \) به این معناست که اگر به اندازۀ کافی \(\Large x \) را به \(\Large a \) نزدیک کنیم، مقدار \(\Large f(x) \) از هر عدد مثبت دلخواهی بزرگتر خواهد شد.
تعریف حد منفی بی نهایت
در صورتی که \(\Large f(x)\) در یک همسایگی محذوف \(\Large a \) تعریف شده باشد، \(\Large \lim\limits_{x\to a} f(x)=-\infty \) به این معناست که اگر به اندازۀ کافی \(\Large x \) را به \(\Large a \) نزدیک کنیم، مقدار \(\Large f(x) \) از هر عدد منفی دلخواهی کوچکتر خواهد شد.
تعریف حدود نامتناهی یک طرفه
در صورتی که \(\Large f(x) \) در یک همسایگی راست \(\Large a\) تعریف شده باشد، \(\Large \lim\limits_{x\to a^+} f(x)=+\infty \) به این معناست که اگر \(\Large x \) را به اندازۀ کافی با مقادیر بزرگتر از \(\Large a \) به \(\Large a \) نزدیک کنیم، مقدار \(\Large f(x) \) از هر عدد مثبت دلخواهی بزرگتر خواهد شد. حد یک طرفۀ نامتناهی چپ و نامتناهی منفی نیز به صورت مشابه تعریف میشود.
مثال 6: حد چپ و راست تابع \(\Large f(x)=\frac{1}{x+3}\) را در نقطۀ \(\Large x=-3 \) به دست آورید.
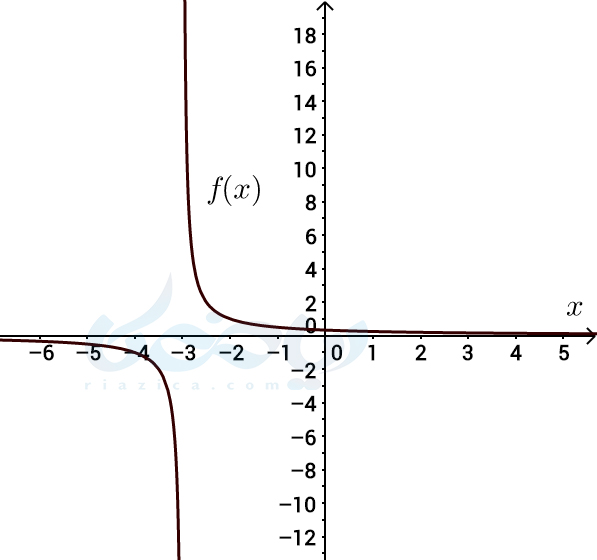
حل: همان طور که از ضابطۀ \(\Large f(x)\) پیداست، زمانی که \(\Large x \) را به \(\Large -3 \) با مقادیر بزرگتر از \(\Large -3 \) نزدیک میکنیم، مخرج نزدیک صفر شده و حد، بی نهایت میشود. از آنجاییکه با مقادیر بزرگتر از \(\Large -3 \) نزدیک شده ایم، علامت کسر مثبت مانده و در نتیجه \(\Large \lim\limits_{x\to-3^+}f(x)=+\infty \). اگر با مقادیر کوچکتر از \(\Large -3 \) به \(\Large -3 \) نزدیک شویم، باز هم مخرج به صفر میل میکند. تفاوت اینجاست که چون با مقادیر کوچکتر از \(\Large -3 \) به \(\Large -3 \) نزدیک شده ایم، علامت کسر منفی است. در نتیجه \(\Large \lim\limits_{x\to-3^-}f(x)=-\infty \). در نمودار تابع \(\Large f(x) \) که در شکل بالا رسم شده است نیز میتوان این مطلب را دید.
چه موقع حد بینهایت میشود؟
تعریف حدود بی نهایت را دیدیم. اما چه زمانی حد یک عبارت، بی نهایت میشود؟
قضیه: فرض کنید \(\Large \lim\limits_{x\to a}g(x)=0 \) و \(\Large \lim\limits_{x\to a}f(x)=L \) که \(\Large L \) یک عدد غیر صفر است. در این صورت، چهار حالت زیر از حالتهای متداولی هستند که حد نامتناهی میشود.
- اگر \(\Large L>0 \) و تابع \(\Large g(x) \) در یک همسایگی محذوف \(\Large a \) مثبت باشد، آنگاه \(\Large \lim\limits_{x\to a}\frac{f(x)}{g(x)}=+\infty \).
- اگر \(\Large L>0 \) و تابع \(\Large g(x) \) در یک همسایگی محذوف \(\Large a \) منفی باشد، آنگاه \(\Large \lim\limits_{x\to a}\frac{f(x)}{g(x)}=-\infty \).
- اگر \(\Large L<0 \) و تابع \(\Large g(x) \) در یک همسایگی محذوف \(\Large a \) مثبت باشد، آنگاه \(\Large \lim\limits_{x\to a}\frac{f(x)}{g(x)}=-\infty \).
- اگر \(\Large L<0 \) و تابع \(\Large g(x) \) در یک همسایگی محذوف \(\Large a \) منفی باشد، آنگاه \(\Large \lim\limits_{x\to a}\frac{f(x)}{g(x)}=+\infty \).
این چهار مورد برای حدود یک طرفه نیز برقرارند.
مثال از حد بی نهایت
مثال 7: حد \(\Large \lim\limits_{x\to \frac{2^+}{3}}\frac{[2x]+1}{-3x+2} \) را محاسبه کنید.
حل: از آنجاییکه از سمت چپ به نقطۀ \(\Large x=\frac{2}{3} \) نزدیک میشویم، مخرج با مقادیر مثبت به صفر میل میکند و حد صورت هم در \(\Large x=\frac{2}{3} \) برابر با \(\Large 2 \) است، طبق قضیۀ قبل، \(\Large \lim\limits_{x\to \frac{2}{3}}\frac{[2x]+1}{-3x+2}=+\infty\).
مثال 8: حد \(\Large \lim\limits_{x\to \frac{\pi^+}{2}}\frac{x+1}{cos x} \) را حساب کنید.
حل: از آنجاییکه با مقادیر بزرگتر از \(\Large x=\frac{\pi}{2} \) به \(\Large \frac{\pi}{2} \) نزدیک میشویم، مخرج با مقادیر منفی به صفر نزدیک میشود. از طرفی حد صورت در \(\Large x=\frac{\pi}{2} \) برابر \(\Large \frac{\pi}{2}+1\) است. بنابراین طبق قضیۀ قبل، \(\Large \lim\limits_{x\to \frac{\pi^-}{2}}\frac{x+1}{cos x}=-\infty \).
در ادامه توصیه میشه پست حد در بی نهایت رو مطالعه کنید.
زنگ آخر کلاس حد بی نهایت
در این درسنامه، ابتدا قسمتی از تقسیم و بخش پذیری چند جمله ای ها و حد توابع کسری را مرور کردیم. سپس، با تعریف همسایگی ، همسایگی محذوف و همسایگی چپ و راست آشنا شدیم. در آخر، حد بی نهایت را معرفی کردیم. چهار حالت از حالتهایی را که حد نامتناهی میشود در قضیۀ آخر درسنامه معرفی کردیم. مثالهای 7 و 8، دو نمونه از این چهار حالت بودند که با یکدیگر بررسی کردیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث حد بینهایت دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.




