حد در بی نهایت ♾✏️ – هر آنچه نیاز دارید بدانید

میدونی حد در بی نهایت چه جوریه؟ قضایاشو میدونی نحوه کارکرد با قضایا رو چی؟ در این درسنامه قصد داریم تا به مبحث حد در بی نهایت بپردازیم. ابتدا یک مثال مهم را با یکدیگر بررسی کرده و حد در بی نهایت را معرفی می‌کنیم. سپس به بررسی قضایا در این زمینه می‌پردازیم.

معرفی حد در بی نهایت

برای اینکه با این نوع حد آشنا شوید، تابع \(\Large  f(x)=\frac{1}{x} \) را در بازۀ \(\Large  (0, +\infty) \) در نظر بگیرید.

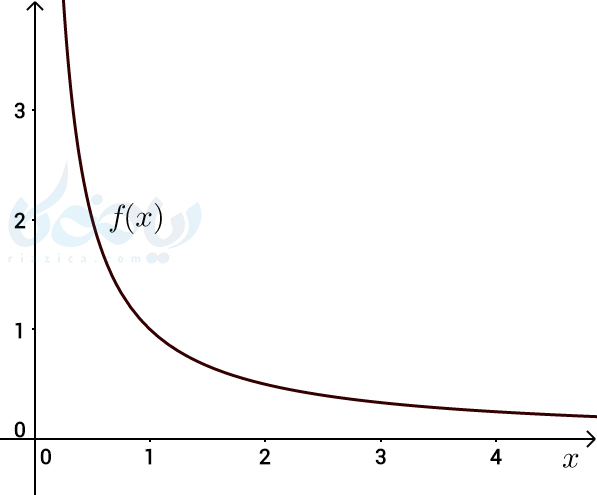
اگر از \(\Large  x=1 \) شروع کرده و به سمت اعداد بزرگتر روی محور \(\Large  x \) حرکت کنیم، مقادیر \(\Large  f(x) \)، رفتاری به صورت زیر خواهند داشت.

همان طور که در جدول بالا می‌بینید. هر چه قدر از مبدأ مختصات دور می‌شویم، مقادیر \(\Large  f(x) \) به 0 نزدیکتر می‌شوند. به عبارت دیگر، اگر \(\Large  x \) را به اندازۀ کافی بزرگ انتخاب کنیم. می‌توانیم به مقدار دلخواه به 0 نزدیک شویم. برای مثال فرض کنید می‌خواهیم فاصلۀ \(\Large  x \) از 0، کمتر از \(\Large  \frac{1}{10^5} \) باشد. در این صورت کافی است \(\Large  x \) را بزرگتر از \(\Large  10^5 \) انتخاب کنیم. در چنین حالتی می‌گوییم حد تابع \(\Large  f(x) \) در مثبت بی نهایت برابر با 0 است. همچنین می‌نویسیم \(\Large  \lim\limits_{x \to +\infty}f(x)=0 \).

این موضوع به طور مشابه برای بازۀ \(\Large  (-\infty, 0) \) نیز برقرار است. یعنی اگر بازۀ \(\Large  (-\infty, 0) \) را در نظر گرفته و از \(\Large  x=-1 \) به تدریج به سمت اعداد بسیار کوچک و منفی حرکت کنیم. مقدار \(\Large  f(x) \) به 0 نزدیک می‌شود. رفتار تابع \(\Large  f(x)\) در بازۀ \(\Large  (-\infty, 0) \)، در جدول زیر پیداست.

همان طور که در جدول بالا می‌بینید، هر چه قدر از مبدأ مختصات دور می‌شویم، مقادیر \(\Large  f(X) \) به 0 نزدیکتر می‌شوند. به عبارت دیگر، اگر \(\Large  x \) را به اندازۀ کافی کوچک انتخاب کنیم، می‌توانیم به مقدار دلخواه به 0 نزدیک شویم. برای مثال فرض کنید می‌خواهیم فاصلۀ \(\Large  f(x) \) از 0، کمتر از \(\Large  \frac{1}{10^5} \) باشد. در این صورت کافی است \(\Large  x \) را کوچکتر از \(\Large  -10^5 \) انتخاب کنیم. در چنین حالتی می‌گوییم حد تابع \(\Large  f(x) \) در منفی بی نهایت برابر با 0 است. همچنین می‌نویسیم \(\Large  \lim\limits_{x \to -\infty}f(x)=0 \).

تعریف حد در بی نهایت

حد در بی نهایت را بر اساس اینکه به سمت \(\Large  +\infty \) یا \(\Large  -\infty \) در حال حرکت هستیم، به صورت زیر تعریف می‌کنیم:

• تابع \(\Large  f(x) \) در بازه‌ای مثل \(\Large  (a, +\infty) \) تعریف شده است. اگر بتوان با انتخاب \(\Large  x \) های به اندازۀ کافی بزرگ، به مقدار دلخواه به عدد \(\Large  L \) نزدیک شد، اصطلاحاً می‌گوییم حد تابع \(\Large  f(x) \) در مثبت بی نهایت برابر با \(\Large L \) است. همچنین می‌نویسیم \(\Large  \lim\limits_{x \to +\infty}f(x)=L \).
• تابع \(\Large  f(x) \) در بازه‌ای مثل \(\Large  (-\infty, b) \) تعریف شده است. اگر بتوان با انتخاب \(\Large  x \) های به اندازۀ کافی کوچک، به مقدار دلخواه به عدد \(\Large  L \) نزدیک شد، اصطلاحاً می‌گوییم حد تابع \(\Large  f(x) \) در منفی بی نهایت برابر با \(\Large L \) است. همچنین می‌نویسیم \(\Large  \lim\limits_{x \to -\infty}f(x)=L \).

قضایا حد در بی نهایت

برای محاسبۀ حد در بی نهایت یک تابع، چند قضیۀ بسیار مهم وجود دارد که در هر زیر عنوان به بررسی یکی از آن‌ها خواهیم پرداخت.

مقدار نامتناهی در مخرج

اگر \(\Large  n \) یک عدد طبیعی باشد، آنگاه:

• \(\Large  \lim\limits_{x \to +\infty}\frac{1}{x^n}=0 \)
• \(\Large  \lim\limits_{x \to -\infty}\frac{1}{x^n}=0\)

به طور مثال \(\Large  \lim\limits_{x \to +\infty}\frac{1}{x^3} \) و \(\Large  \lim\limits_{x \to -\infty}\frac{1}{x^3} \) برابر با صفر هستند.

حد عملیات اصلی بین توابع در بی نهایت

اگر \(\Large  \lim\limits_{x \to +\infty}f(x)=m \) و \(\Large  \lim\limits_{x \to +\infty}g(x)=n \)، آنگاه:

• \(\Large  \lim\limits_{x \to +\infty}(f(x)\pm g(x))=m \pm n \)
• \(\Large  \lim\limits_{x \to +\infty}(f(x) g(x))=mn \)
• \(\Large  \lim\limits_{x \to +\infty}\frac{f(x)}{g(x)}=\frac{m}{n} (n \neq 0) \)

این قضیه برای حالتی که \(\Large  x \to -\infty\) نیز صادق است. به عبارت دیگر، حد جمع و ضرب و تقسیم توابع در بی نهایت برابر است با جمع و ضرب و تقسیم حد آن‌ها در بی نهایت ( دقت کنید که حد مخرج تقسیم باید مخالف صفر باشد).

مثال 1: مقدار \(\Large  \lim\limits_{x \to +\infty}\frac{3x^2+2x+5}{4x^2+6x+1} \) را محاسبه کنید.

حل: برای محاسبۀ حد چنین توابعی در قسمت بعد قضیه‌ای معرفی می‌کنیم که کار ما را بسیار آسان خواهد کرد. اما با استفاده از دو قضیه‌ای که تا اینجا خواندیم نیز می‌توانیم مقدار این حد را به دست آوریم. برای این کار کافی است بزرگترین توان \(\Large  x \) را که در صورت و مخرج موجود است، از صورت و مخرج فاکتور گرفته و با استفاده از قضایای قبل، حد را به صورت زیر محاسبه کنیم.

\(\LARGE  \lim\limits_{x \to +\infty}\frac{3x^2+2x+5}{4x^2+6x+1} \)

\(\LARGE  =\lim\limits_{x \to +\infty}\frac{x^2(3+\frac{2}{x}+\frac{5}{x^2})}{x^2(4+\frac{6}{x}+\frac{1}{x^2})} \)

\(\LARGE  =\frac{\lim\limits_{x \to +\infty}(3+\frac{2}{x}+\frac{5}{x^2})}{\lim\limits_{x \to +\infty}(4+\frac{6}{x}+\frac{1}{x^2})} \)

\(\LARGE  =\frac{\lim\limits_{x \to +\infty}3+\lim\limits_{x \to +\infty}\frac{2}{x}+\lim\limits_{x \to +\infty}\frac{5}{x^2}}{\lim\limits_{x \to +\infty}4+\lim\limits_{x \to +\infty}\frac{6}{x}+\lim\limits_{x \to +\infty}\frac{1}{x^2}} \)

\(\LARGE  =\frac{3+0+0}{4+0+0} =\frac{3}{4}\)

حد توابع چند جمله‌ای در بی نهایت

فرض کنید \(\Large  n \) یک عدد طبیعی و \(\Large  a \) یک عدد حقیقی غیر صفر باشد. در این صورت، اگر داشته باشیم:

\(\Large f(x)=ax^n+bx^{n-1}+ \dots+ k\)

آنگاه \(\Large  \lim\limits_{x \to +\infty}f(x)=\lim\limits_{x \to +\infty}ax^n \) و \(\Large  \lim\limits_{x \to -\infty}f(x)=\lim\limits_{x \to -\infty}ax^n \). به عبارت دیگر حد یک تابع چند جمله ای مانند \(\Large f(x) \) در بی نهایت برابر است با حد جمله ای که بیشترین توان را دارد (در صورتی که مبحث چند جمله ای ها را فراموش کرده‌اید، به درسنامۀ تابع چند جمله ای به زبان ساده مراجعه کنید).

مثال 2: حد موجود در مثال 1 را این بار با استفاده از قضیه‌ای که بیان کردیم به دست آورید.

حل:

\(\LARGE  \lim\limits_{x \to +\infty}\frac{3x^2+2x+5}{4x^2+6x+1} \)

\(\LARGE  =\frac{\lim\limits_{x \to +\infty}(3x^2+2x+5)}{\lim\limits_{x \to +\infty}(4x^2+6x+1)} \)

\(\LARGE  =\frac{\lim\limits_{x \to +\infty}(3x^2)}{\lim\limits_{x \to +\infty}(4x^2)} \)

\(\LARGE  =\lim\limits_{x \to +\infty}\frac{3x^2}{4x^2} \)

\(\LARGE  =\frac{3}{4} \)

حد نامتناهی در بی نهایت

حد برخی از توابع در بی نهایت، یک مقدار نامتناهی می‌شود. به طور مثال، تابع \(\Large  f(x)=x \) را در نظر بگیرید. اگر مقدار \(\Large  x \) را به سمت اعداد بسیار مثبت نزدیک کنیم، مقدار \(\Large  f(x) \) به صورت زیر تغییر می‌کند.

همان طور که در جدول بالا می‌بینید، اگر مقدار \(\Large  x \) را به اندازۀ کافی بزرگ کنیم، \(\Large  f(x) \) به مقدار دلخواه بزرگ خواهد شد. مثلا اگر به دنبال \(\Large  f(x) \) با مقادیر بزرگتر از \(\Large  10^6 \) باشیم، کافی است \(\Large  x \) را بزرگتر از \(\Large  10^6 \) در نظر بگیریم. در این حالت می‌نویسیم \(\Large  \lim\limits_{x \to +\infty} f(x)=+\infty\). همین کار را برای \(\Large  x \) های بسیار کوچک نیز می‌توان انجام داد. در جدول زیر رفتار \(\Large  f(x) \) به ازای \(\Large  x \) های بسیار کوچک نشان داده شده است.

همان طور که از جدول بالا پیداست، اگر \(\Large  x \) را به اندازه‌ی کافی کوچک در نظر بگیریم، \(\Large  f(x) \) از هر عدد منفی کوچکتر خواهد شد. مثلا اگر به دنبال \(\Large  f(x) \) با مقادیر کوچکتر از \(\Large  -10^6 \) باشیم، کافی است \(\Large  x \) را کوچکتر از \(\Large  -10^6 \) در نظر بگیریم. در این حالت می‌نویسیم \(\Large  \lim\limits_{x \to -\infty} f(x)=-\infty \).

تعریف حد نامتناهی در بی نهایت

حد نامتناهی در بی نهایت به صورت زیر تعریف می‌شود:

• تابع \(\Large  f(x) \) در بازۀ \(\Large  (a, +\infty) \) تعریف شده است. اگر با انتخاب \(\Large  x \) های به اندازۀ کافی بزرگ، \(\Large  f(x) \) از هر عدد مثبت دلخواهی بزرگتر شود، می نویسیم \(\Large  \lim\limits_{x \to +\infty} f(x)=+\infty \).
• تابع \(\Large  f(x) \) در بازۀ \(\Large  (-\infty, a) \) تعریف شده است. اگر با انتخاب \(\Large  x \) های به اندازۀ کافی کوچک، \(\Large  f(x) \) از هر عدد منفی دلخواهی کوچکتر شود، می نویسیم \(\Large  \lim\limits_{x \to -\infty} f(x)=-\infty\).

دو رابطۀ \(\Large  \lim\limits_{x \to +\infty} f(x)=-\infty \) و \(\Large  \lim\limits_{x \to -\infty} f(x)=+\infty \) نیز به صورت مشابه تعریف می‌شوند.

مثال 3: نمودار تابع \(\Large  f(x) \) در شکل زیر رسم شده است. مقدار \(\Large  \lim\limits_{x \to +\infty} f(x) \) و \(\Large  \lim\limits_{x \to -\infty} f(x)\) را بیابید.

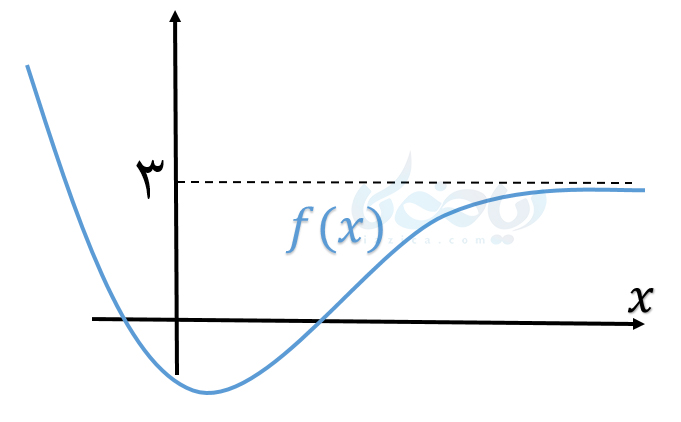
حل:همان طور که ار نمودار \(\Large  f(x) \) پیداست، به ازای \(\Large  x \) های بسیار بزرگ، \(\Large  f(x) \) به عدد 3 نزدیک می‌شود. بنابراین \(\Large  \lim\limits_{x \to +\infty} f(x)=3 \). اما به ازای \(\Large  x \) های به اندازۀ کافی کوچک، \(\Large  f(x)\) از هر عدد مثبت دلخواهی بزرگتر می‌شود. بنابراین \(\Large  \lim\limits_{x \to -\infty} f(x)=+\infty \).

حد در بی نهایت تابع یک جمله‌ ای

اگر \(\Large  f(x)=x^n \) باشد، آنگاه \(\Large  \lim\limits_{x \to +\infty} f(x)=+\infty \). در صورتی که \(\Large  f(x) \) را در یک عدد ثابت غیر صفر مثل \(\Large  a \)ضرب کنیم، بازهم حد \(\Large  f(x) \) در بی نهایت، نامتناهی شده و علامت آن برابر با علامت \(\Large  a \) خواهد بود. مثلا، اگر \(\Large  f(x)=x^3 \) باشد، داریم:

\(\LARGE \lim\limits_{x \to +\infty} x^3=+\infty \)

\(\LARGE \lim\limits_{x \to +\infty} 2x^3=+\infty \)

\(\LARGE \lim\limits_{x \to +\infty}( -2x^3)=-\infty \)

در صورتی که بخواهیم \(\Large  \lim\limits_{x \to -\infty} x^n\) را حساب کنیم، پاسخ بسته به زوج و فرد بودن \(\Large  n \) متفاوت خواهد بود. در واقع \(\Large  -\infty \) با اینکه یک عدد حقیقی نیست، اما مانند یک عدد حقیقی منفی رفتار می کند. مثلا، اگر \(\Large  f(x)=x^2 \) باشد، \(\Large  \lim\limits_{x \to -\infty} x^2=+\infty\) اما \(\Large  \lim\limits_{x \to -\infty} x^3=-\infty\).

زنگ آخر کلاس

در دسنامه‌ای که با یکدیگر خواندیم، ابتدا حد در بی نهایت را معرفی کردیم. سپس، چند قضیه‌ی بسیار مهم را بررسی کردیم. با به کار گیری این قضیه‌ها می‌توانیم به سوالات مبحث حد در بی نهایت پایه دوازدهم تجربی پاسخ دهیم. در انتهای درسنامه نیز به مبحث حد نامتناهی در بی نهایت پرداختیم. تمامی آموزش‌های ریاضی دوازدهم تجربی رو میتوانید داخل سایت ببینید.

ما در ریاضیکا آماده‌ی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با این مبحث دارید، در دیدگاه‌ها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند ‌داد.