آموزش ریاضی پایه یازدهم تجربی
آموزش حل لگاریتم : تمام آنچه که باید یاد بگیرید ✳️📝
با سلام به دوستان ریاضیکا در درسنامه اموزش تابع لگاریتمی-تابع معکوس موفقیت ،مفهوم لگاریتم ،تابع لگاریتمی ورسم تابع لگاریتمی را فرا گرفتیم .حال در این پست سعی داریم با قوانین لگاریتم آشنا شویم وبا استفاده از این قوانین مقدار لکاریتم یک عدد را بدست آوریم ومعادلات لگاریتمی را حل نماییم.
آموزش حل لگاریتم از مفاهیم جذابی است که در کتاب ریاضی یازدهم عنوان شده است. در این نوشتار میخواهیم این مفهوم مهم را با 12 قانونش و اثباتشان یاد بگیریم.
تعریف لگاریتم :
تابع نمایی زیر را در نظر بگیرد:
![]()
چون این تابع یک تابع یک به یک است پس وارون پذیر است. وارون آن یک تابع لگاریتمی است که به صورت زیر نمایش داده میشود.
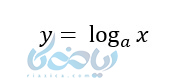
حال با توجه به تعریف لگاریتم و ویژگیهای زیر به آموزش حل لگاریتم و اثبات بعضی از این ویژگی ها می پردازیم.

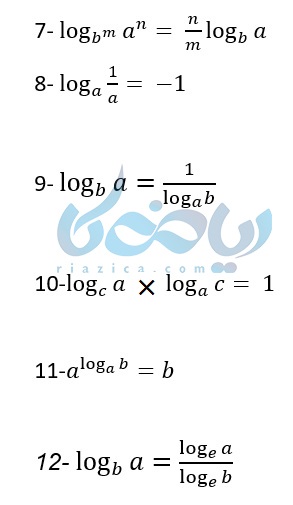
اثبات روابط لگاریتمی
اثبات 3:
\( \LARGE log_c a + log_c b = log_c ab \)
فرض کنیم:\( \Large log_c a = m , log_c b = n \)
\( \LARGE \begin{cases} log_c a = m \rightarrow c^m = a \\ log_c b = n \rightarrow c^n = b \end{cases} \)
طرفین رابطه را درهم ضرب میکنیم:
\( \LARGE c^m \times c^n = ab \)
\( \LARGE c^{m+n} = ab \)
از طرفین لگاریتم میگیریم:
\( \LARGE log_c ab = m + n \)
پس طبق فرض داریم:
\( \LARGE log_c ab = log_c a + log_c b \)
اثبات 4:
\( \LARGE log_c a – log_c b = log_c \frac{a}{b} \)
فرض کنیم:\( \Large log_c a = m , log_c b = n \)
\( \LARGE \begin{cases} log_c a = m \rightarrow c^m = a \\ log_c b = n \rightarrow c^n = b \end{cases} \)
طرفین رابطه را به هم تقسیم، میکنیم:
\( \LARGE c^{m – n}= \frac{a}{b} \)
از طرفین لگاریتم میگیریم:
\( \LARGE log_c \frac{a}{b} = m – n \)
پس طبق فرض داریم:
\( \LARGE log_c \frac{a}{b} = log_c a – log_c b \)
اثبات رابطه ۵:
البته این رابطه بسته به اینکه توان آن چه نوع عددی است، اثباتهای متفاوتی دارد. ما در این مرحله آن را عضو اعداد طبیعی \( \Large n \in \mathbb{N} \) فرض و به صورت زیر اثبات میکنیم:
\( \LARGE log_b a^n = nlog_b a \)
طرف اول:
\( \LARGE log_b a^n \)
\( \LARGE = log_b {a \times a \times a … \times a} \)
طبق رابطه 3:
\( \LARGE log_b a + log_b a + ..+ log_b a \)
\( \LARGE = nlog_b a \)
مثال 1: حاصل عبارت های زیر را به دست آورید.
الف)
\( \LARGE log_{100} {0.001} + 3log_{32} {64} \)
\( \LARGE – log_{2} {\sqrt2} = ? \)
حل 1 الف:
\( \LARGE log_{100}{0.001} + 3log_{32}{64} \)
\( \LARGE – log_{2}{\sqrt2} \)
\( \LARGE = log_{10^2}{10^{-3}} + 3log_{2^5}{2^6} \)
\( \LARGE – log_{2}{2^{\frac{1}{2}}} \)
\( \LARGE = -\frac{3}{2}log_{10}{10} + \frac{18}{5}log_{2}{2} \)
\( \LARGE – \frac{1}{2}log_{2}{2} \)
\( \LARGE = \frac{-15+36-5}{10} = \frac{16}{10} = 1.6 \)
ب)
\( \LARGE log_{\sqrt5} {125} + 2log_{27} {81} \)
\( \LARGE – log_{\sqrt2} {\sqrt8} = ? \)
حل 1 ب:
\( \LARGE log_{\sqrt5} {125} + 2log_{27} {81} \)
\( \LARGE – log_{\sqrt2} {\sqrt8} \)
\( \LARGE = log_{5^{\frac{1}{2}}} {5^{3}} – 2log_{3^3} {3^4} \)
\( \LARGE – log_{2^{\frac{1}{2}}} {2^{\frac{3}{2}}} \)
\( \LARGE = 6 – \frac{8}{3} – 3 = \frac{1}{3} \)
نکته ۱: اگر مبنای لگاریتم عدد ۱۰ باشد آن را نمی نویسیم. مانند فرجه ۲ یا توان را \( \Large log_{10} {5} = log_{} {5} \) که به آن لگاریتم اعشاری می گویند.
مثال 2: اگر \( \LARGE log_{} {3} = a , log_{} {2} = b \) باشد، مقدار عبارت زیر را بر حسب \( \Large a \) و \( \Large b \) بدست آورید.
\( \LARGE log_{} {\frac{24}{\sqrt18}} = ? \)
حل 2:
\( \LARGE log_{} {\frac{24}{\sqrt18}} \)
\( \LARGE = log_{} {24} – log_{} {\sqrt18} \)
\( \LARGE = log_{}( {2^3} \times 3) – log_{} {18^{\frac{1}{2}}} \)
\( \LARGE = log_{} {2^3} + log_{} {3} \)
\( \LARGE – \frac{1}{2}log_{}( {3^2} \times 2) \)
\( \LARGE = 3log_{} {2} + log_{} {3} \)
\( \LARGE – \frac{1}{2}(2log_{} {3} + log_{} {2}) \)
\( \LARGE = 3b + a- a- \frac{1}{2}b \)
\( \LARGE = \frac{5}{2}b \)
محاسبه لگاریتم مطلبی مهم است که باید از ویژگی های لگاریتم برای محاسبهٔ آن استفاده کنیم. مثالهای بالا نیز از همین دسته بودند.
آموزش حل لگاریتم: معادلات لگاریتمی
یکی از مهمترین کاربردهای لگاریتم حل معادلات لگاریتمی است که معمولاً از مدلسازی یک مسئله واقعی بدست می آید. برای کاربرد حل معادلات لگاریتم میتوان به مثالهای زیر اشاره کرد:
- محاسبه شدت زلزله
- مشخص کردن ضعیفترین صدای قابل شنیدن یا آستانه شنوایی
- پیشبینی جمعیت یک جامعه پس از زمان مشخص
- محاسبه نیمه عمر عناصر رادیواکتیو
- محاسبه طول عمر یافتههای باستانشناسی
حل معادله لگاریتمی
به طور کلی اگر \( \Large a \) عدد حقیقی مثبت \( \Large a \neq 1 \) باشد، آنگاه با توجه به یک به یک بودن تابع لگاریتمی، از تساوی \( \Large log_{a} {x} = log_{a} {y} , (x , y) > 0 \) میتوان نتیجه گرفت : \( \Large x = y \) و بر عکس.
اگر \( \Large x = y \) آنگاه \( \Large log_{a} {x} = log_{a} {y} , (x , y) > 0 \).
در مبحث آموزش حل معادله لگاریتم باید یکی از دو حالت زیر برقرار باشد:
- یک طرف لگاریتم و طرف دوم یک عدد باشد و بعد با تبدیل معادله به یک معادله نمایی آن را حل میکنیم
- دو طرف دو لگاریتم هم بنا باشند تا از خاصیتی که بالا گفتیم استفاده شود.
مثال 3: \( \Large x \) را در معادلات زیر پیدا کنید.
الف)
\( \Large log_{3} {x} = 2 \rightarrow x=? \)
حل 3 الف:
\( \LARGE log_{3} {x} = 2 \)
\( \LARGE x = 3^2 = 9 \)
ب)
\( \Large log_{5} {(x+6)} = log_{5} {(2x-3)} \)
\( \Large \rightarrow x = ? \)
حل 3 ب:
\( \LARGE log_{5} {(x+6)} = log_{5} {(2x-3)} \)
\( \LARGE x + 6 = 2x – 3 \)
\( \LARGE \rightarrow x = 9 \)
ج)
\( \Large log_{5} {(x+1)} + log_{5} {(x-1)}= 1 \)
\( \Large \rightarrow x = ? \)
حل 3 ج:
\( \LARGE log_{5} {(x+1)} \)
\( \LARGE + log_{5} {(x-1)}= 1 \)
\( \LARGE log_{5} {(x^2-1)} = 1 \)
\( \LARGE x^2 – 1 = 5^1 \)
\( \LARGE x^2 = 6 \)
\( \LARGE \rightarrow x =\pm \sqrt6 \)
کاربرد های آموزش حل لگاریتم در زندگی روزمره
لگاریتم در زندگی امروز کاربردهای زیادی دارد و در هر رشته و هر شغلی فوایدش بسیار است. بعنوان مثال از آموزش حل لگاریتم و یادگرفتن رسم آن غیر از ریاضی میتوان به کاربرد آن در علوم مختلف اشاره کرد:
- مهندسی شیمی و در بحث \( \Large PH \) برای تشخیص بازی و اسیدی مایعات اشاره کرد کاربرد فراوان و به ویژهای دارد.
- لگاریتم در بحث زلزله و تعیین دامنه آن نیز کاربرد دارد.
- دانشمندان نیز برای بیان زلزله از مقیاس ریشتر استفاده می کنند که از بحث لگاریتم گرفته شده است.
- در بحث اخترشناسی فاصلهٔ بین ستارگان و سیاره ها نیز به کار میرود.
- در بحث موسیقی برای بیان سطح فشار صوت و سنجش فواصل موسیقی نیز از لگاریتم استفاده می گردد.
- در باستانشناسی با استفاده از روش سالیابی کربن 14، میتوان عمر یک اثر باستانی را محاسبه کرد. در این روش، تعیین قدمت اثر با یک تابع لگاریتمی مدلسازی می شود.
به طور کلی میتوان گفت هرجایی که با عددهایی که توان آن بسیار کوچک و یا بسیار بزرگ است، از لگاریتم استفاده میکنیم.
توصیه می شود حتما قبل از خواندن این پست درسنامه تابع لگاریتمی-تابع معکوس موفقیت را مطالعه کنید.
کلام آخر در آموزش حل لگاریتم
در این آموزش از مجموعه آموزشهای ریاضی یازدهم تجربی، باهم در مورد آموزش حل لگاریتم، ۱۲ قانون مهم آن و اثبات مهمترین قانونهایش صحبت کردیم. همچنین مثالهای مختلفی را باهم بررسی کردیم. در انتها نیز کاربردهای مختلف و متنوعی از حل لگاریتم در زندگی انسان امروز بیان شد.
در صورتیکه هرگونه سوالی از این بخش دارید، میتوانید سوال خود را در بخش دیدگاهها در پایین همین قسمت برای ما مطرح کنید. ما در ریاضیکا به سوالات شما عزیزان پاسخ خواهیم داد.





سلام
خواستم بگم فرمولای خوبی گذاشتید ممنون اما ابتدا فرمول ساده شده رو اشتباه گذاشتید چون وقتی y=a^x باشه میشه Log a y = x نه اینکه y=Log a x لطفا تصحیح بفرمائید
سلام و عرض ادب
در اصل این x , y معکوس شده x,y اصلی هستند یعنی x لوگاریتم y تابع نمایی است و y آن x تابع نمایی است در تابع معکوس آن ها را جابجا کرده و اسمشان را عوض می کنیم.
موفق باشید
سلام خسته نباشید Log این عبارت چطوری حساب میکنید
a+(48-a)exp(-b(x-8))
سلام و عرض ادب
ممنون از نگاهتون. ببخشید برای ما خوانا نبود ممنون میشم واضح تر بنویسید.
موفق باشید.
سلام میختاستم تشکر کنم از سایت کاربردی و بروزتون?⚘
سلام عرض ادب
ممنون از انرژی که دادید.
موفق باشید.
سلام
برای پایه لگاریتم غیر از به شکل اعداد تواندار نویسی ، کار دیگه ای هم میشه انجام داد؟
سلام و عرض ادب
برای ساده کردن لگاریتم ها بهترین راه همان توان دار نویسی می باشد.
موفق باشید.
سلام خسته نباشید من لگاریتم رو برا آزمون استخدامی در حد ساده میخواستم میشه کمکم کنید ؟ زیاد وقت ندارم? در حد ریشه معادله و جواب معادله و از این چیزای ساده
سلام و عرض ادب
متاسفانه نمیتونیم در امتحانات کمک کنیم.
درسنامه ما با زبان ساده این مبحث توضیح داده، بخونید مشکلی بود ما پاسخگو هستیم.
موفق باشید
سلام .. ممنون از توضیحاتی که در سایت قرار دادید، یه سوال داشتم ، لگاریتم n در پایه 4 چه جوابی داره؟ یا به چه فرمتی میتونیم بنویسیمش؟ممنون
با عرض سلام و درود
چون این یک عبارت است نه معادله پس جواب ندارد. منظورتون از فرمت چیست؟
موفق باشید
سلام خسته نباشید ممنون میشم اگه این عبارت لگاریتم رو جواب بدید.Log (2+3+7
با سلام
باید این اعداد رو جمع کنید بعد ۱۲ رو تجزیه کنید در نهایت میشه دوتا لگاریتم ۲بعلاوه لگاریتم ۳
سلام. ممنون میشم اگه این لگاریتم وجواب بدید.
لگاریتم ۳ ایکس منها یک مساوی دو. log3x_1=2
سلام وعرض ادب
کافیه به تابع نمایی تبدیل کنید میشه 3x-1=100 حالا این معادله رو حل میکنیم جواب میشه ۳۳
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
این درسته که از هر عبارت که لگاریتم میگیریم اون عبارت فاقد واحد میشه؟ به عنوان مثال Ph چون لگاریتم میگیریم واحد نداره
با سلام وعرض ادب
بله درسته
سلام خسته نباشید
ببخشید میشه توضیحاتی هم درباره لگاریتم گرفتن از طرفیت بدین?
چرا تمام قوانین لگارتم وجود نداره وهمچنان اثبات انها نیز وجود نداره
با سلام واحترام
فقوانین واثباتهایی که برای پایه یازدهم لازمه همگی نوشته شده
کاش با لحنی زیباتر بیان میکردید چون ما زحمت زیادی برای سایت میکشیم
یچبا سلام و احترام
از این که با زبان ساده،کامل، گویا و روان دانش خودتون رو اینجا در اختیار ما گذاشتید بینهایت سپاسگزارم. کمک بزرگی برای من بود و خوشحال شدم با سایت مفیدتون آشنا شدم. قطعاً از بقیه قسمتهای سایت هم استفاده خواهم کرد. موفق باشید.
با سلام واحترام
با شنیدن چنین نظرات خوشحالروخرسند میشیم وشاکر خداوندیم که رسالتمون رو در آموزش دانش آموزان سرزمینمون انجام داده ایم
سلام وقتتون بخیر می خواستم بپرسم برای تبدیل log2x- به جمع منفی پشت عبارت به چه صورت تاثیر میکنه؟
آیا به این شکل میشه log2+logx- یا منفی باید در هر دو تاثیر بذاره؟
با سلام
چون پرانتز نداره روی لگاریتم بعدی تاثیر نداره
سلام و وقت بخیر
ممنون از اطلاعات خوبتون
میخواستم بدونم روش حل معادله هایی مثل
X^logx= 1000 (ایکس به توان لگاریتم ایکس در مبنای ۱۰ مساوی ۱۰۰۰) چطور حل میشن؟
سلام خسته نباشید میشه لطفا اثبات رابطه ۱۰ رو مگین لطفا
سلام دوست عزیز
طبق ۹ این دو تا معکوس یکدیگرند پس حاصلضربشان یک می شود.
با سلام
لذت بردم از سایت خوبتون به راه تون ادامه بدید
با سلام وادب
ممنون از نگاه وانرٰٰژی که به ما می دهید.
باسلام خدمتتون دستتون درد نکنه همه چی کامل بود فقط یه چیز رو جا انداختید که اگر لگاریتم توی توان یک عدد باشه جای اون عدد با آرگومان قابل تعویضه مثلا
10 به توان2 logمیتونه نوشته بشه ۲ به توان log 10 که کلا میشه ۲.
با سلام
ممنون از یاد آوری شما
چند مثال برای لگاریتم
با سلام log5 چگونه حل میشود ؟
لگ ۱۰ تقسیم بر دو میشه یک منهای لگ دو
سلام
ببخشید استاد
log رادیکال ۵ برمبنای ۵ چند میشه
سلام میشود یک دوم