آموزش تابع نمایی – تابع موفقیت ✳️📶

در سالهای گذشته با توان و خواص اعداد توان دار آشنا شدید . حال می‌خواهیم با آموزش تابع نمایی و لگاریتمی آشنا شویم. می‌دانید اسم دیگر توان نما است. تابع نمایی یک تابع توانی است. تابع وارون تابع نمایی، تابع لگاریتمی است که این توابع در ریاضیات، فیزیک، شیمی، عمران و دیگر رشته‌ها کاربرد زیادی دارد.

تعریف تابع نمایی

تابعی است که متغیر در توان قرار دارد و نمایش آن به صورت زیر خواهد بود:

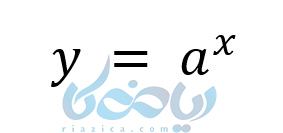
که در آن \( \Large a \) عددی مثبت و مخالف صفر است. دامنه تابع نمایی اعداد حقیقی و برد آن اعدد صحیح مثبت است. مانند:

---

---

 رسم نمودار تابع نمایی به روش نقطه یابی

تابع زیر را در نظر بگیرید :

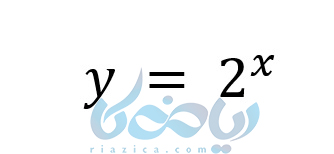
به کمک آموزش تابع نمایی می‌خواهیم ببینیم نمودار این تابع به به چه شکلی خواهد بود. با استفاده از روش نقطه یابی نمودار آن را باهم رسم می‌کنیم.

2	1	۰	-1	-2	x
4	2	1	\( \Large \frac{1}{2} \)	\( \Large \frac{1}{4} \)	y

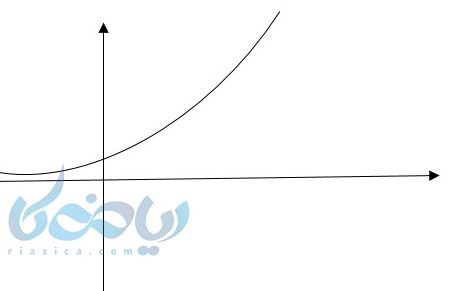
به طور کلی وقتی \( \Large a \) به صورت زیر باشد نمودار آن صعودی است:
(\( \LARGE a>1 \))

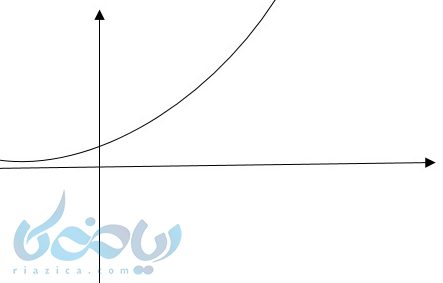
که محور  \( \Large y \) را در نقطه یک قطع کرده و محور \( \Large x \)ها را اصلاً قطع نمی‌کند.

مثال ۱: تابع زیر را رسم کنید؟

\( \LARGE y = (\frac{1}{2})^x \)

حل ۱: به کمک آموزش تابع نمایی و نقطه یابی نمودار زیر را رسم می کنیم.

 

2	1	۰	-1	-2	x
\( \Large \frac{1}{4} \)	\( \Large \frac{1}{2} \)	1	2	4	y

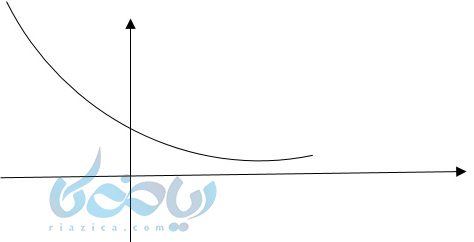
به طور کلی وقتی \( \Large a \) به صورت زیر باشد نمودار نزولی است. شکلش به صورت زیر است:
(\( \LARGE 0<a<1 \))

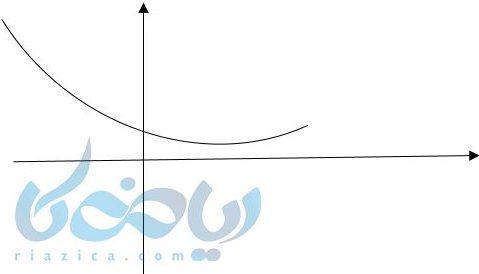
که محورها را قطع نکرده و محوری \( \Large y \)ها را باز در یک نقطه قطع می‌کند.
اما تابع نمایی به صورت های زیر می تواند باشد:

\( \Large y = (\frac{1}{2})^{x+1} – 2 \)

\( \Large y = 2^{x} – 1 \)

\( \Large y = 2^{x – 9} \)

سوال ۲: آیا هر بار برای رسم نمودار تابع نمایی لازم است با تعداد نقاط پیشماری آنها را رسم می کنیم؟

پاسخ ۲: خیر. همانطور که تا به این لحظه از آموزش تابع نمایی آموختیم، با استفاده از سه نقطه و شناختی که از نمودارهای پایهٔ یا به قولی نمودارهایی مادر پیدا کرده‌ایم، آن‌ها را رسم می‌کنیم. برای این کار مراحل زیر را طی خواهیم کرد:

1. ابتدا ریشه توانی را پیدا کرده.
2. عدد به دست آمده را به جای \( \Large x \) گذاشته و \( \Large y \) آن نقطه را نیز پیدا می‌کنیم. مثلاً در رابطهٔ زیر ریشهٔ توان \( \Large x = 1 \) است که به ازای آن \( \Large y = 1 \) می‌شود.
3. در نهایت این نقطه را وسط جدول نوشته و یک نقطه قبل و بعد این \( \Large x \) را نوشته و دو نقطه کمکی برای رسم پیدا می‌کنیم.

\( \LARGE y = 2^{x-1} \)

2	1	۰	x
2	1	\( \Large \frac{1}{2} \)	y

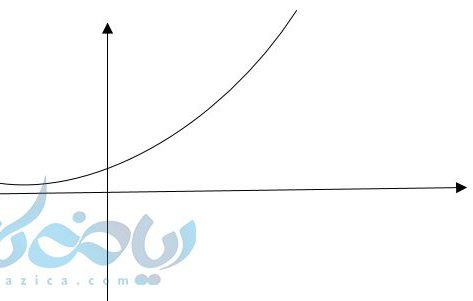
البته همانطور که می‌بینید هرچقدر \( \Large x \)ها به طرف منفی بینهایت می‌روند، \( \Large y \) به صفر نزدیک و نزدیک‌تر می‌شود ولی هیچ گاه صفر نمی شود. پس محور \( \Large x \)ها را قطع نمی‌کند و کنار آن به سمت بی‌نهایت می‌رود. بعدها که مفهوم حد در بی نهایت را خواندید متوجه خواهید شد که به این خط، خط مجانب می‌گویند که نمودار کنار آن به سمت بی‌نهایت می‌رود.

رسم نمودار تابع نمایی به روش انتقال

اما می توان به روش دیگری به نام روش انتقال نمودارهایی شبیه نمودار بالا را رسم کردما دو نوع انتقال داریم :

1. انتقال افقی
2. انتقال عمودی

برای رسم نمودار به روش انتقال ابتدا نمودار اصلی (مادر) را رسم می کنیم سپس با توجه به ضابطه تابع آن را منتقل می کنیم در مثال بالا چون مبنای تابع ۲ می باشد پس نمودار اصلی آن به صورت \( \LARGE y = 2^{x} \) است که به صورت زیر رسم می شود:

\( \LARGE y = 2^{x} \)

1	۰	-1	x
2	1	\( \Large \frac{1}{2} \)	y

\( \Large x = 0 \) ریشه توانی است.

انتقال افقی

حال اگر بخواهیم نمودار تابع \( \LARGE y = 2^{x-1} \) را رسم کنیم  چون \( \Large x \) منهای یک شده، ما نمودار زیر را یک واحد به سمت راست منتقل می‌کنیم .در اصل به \( \Large x \)ها یک واحد اضافه می‌شود، ولی \( \Large y \)‌ها تغییر نمی‌کنند.

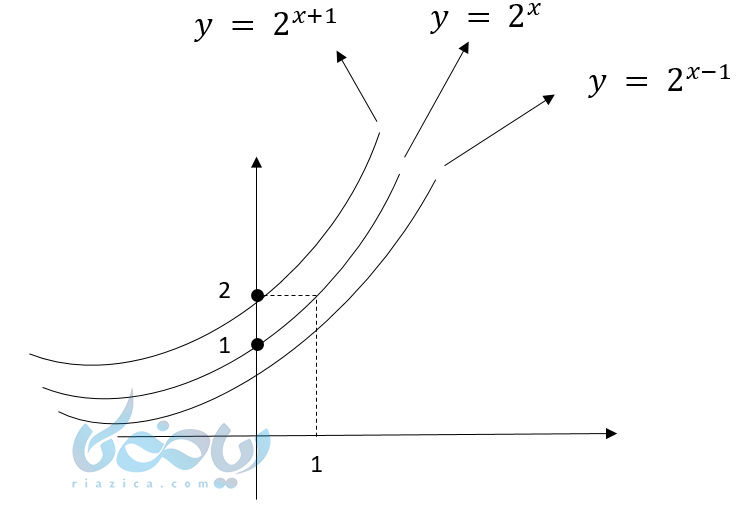
البته راه نقطه‌یابی همواره بهتر و راحت‌تر است. حال اگر نمودار \( \Large y = 2^{x+1} \) را بخواهیم از راه انتقال رسم کنیم، باید نمودار را یک واحد به سمت چپ منتقل می کنیم که نمودار \( \Large y = 2^{x} \) بدست می‌آید. این نمودار در شکل بالا قابل مشاهده است.

انتقال عمودی

اما اگر داشته باشیم \( \Large y = 2^{x} + 1 \)، از راه انتقال نمودار یک واحد به سمت بالا می‌رود. در چنین حالت‌هایی، دیگر خط مجانب محور \( \Large x \)ها نمی‌شود. بلکه خط \( \Large  y = 1 \) می‌شود. چون هر مقداری به \( \Large x \) بدهیم وقتی عدد 2 به توان آن برسد و با عدد یک جمع شود، همیشه مقدار این تابع از یک بیشتر است. پس داریم:

1	۰	-1	x
3	2	\( \Large 1\frac{1}{2} \)	y

پس در رسم نمودار دقت کنیم و اجازه ندهیم نمودار از خط \( \Large y = 1 \) پایین‌تر بیاید.

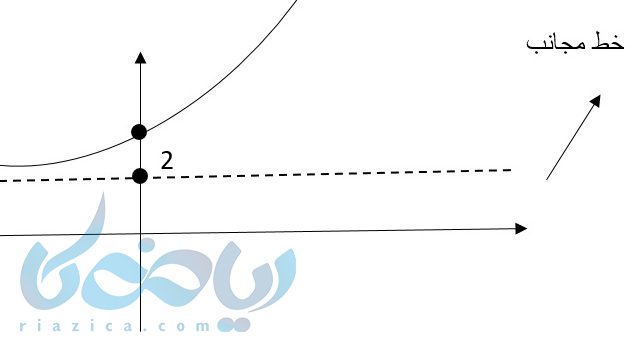
نمودار تابع \( \Large y = 2^{x-1} + 2 \) را در نظر بگیرید. برای رسم این نمودار از راه انتقال نمودار تابع \( \Large y = 2^{x} \) را یک واحد به سمت راست و دو واحد به سمت بالا انتقال می‌دهیم. ولی همانطور که گفتیم راه نقطه‌یابی بهتر است.

ریشه توان و یک نقطه قبل و بعد آن را پیدا می کنیم. خط مجانب این تابع \( \Large y = 2 \) است. برای رسم این نمودار از راه انتقال نمودار تابع:

2	1	۰	x
4	3	\( \Large 2\frac{1}{2} \)	y

مثال ۳: نمودار زیر را رسم کنید؟

\( \LARGE y = 2^{x+2} -1\)

حل ۳: به کمک آموزش تابع نمایی و نقطه یابی نمودار زیر را باهم رسم می‌کنیم.

خط مجانب \( \Large y = -1 \) است.

 

-1	-2	-3	x
1	۰	\( \Large -\frac{1}{2} \)	y

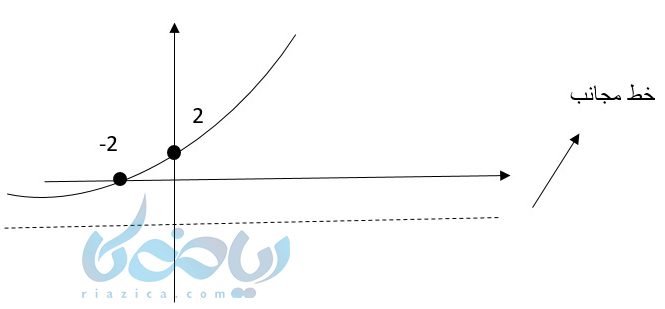
اگر بخواهیم این تابع را به روش انتقال رسم کنیم هم انتقال افقی وهم انتقال عمودی داریم دو احد به سمت چپ و یک واحد به سمت پایین

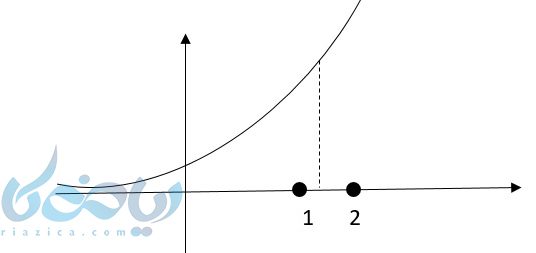
مثال ۴: با استفاده از نمودار تابع، \( \Large y = 4^x \) مقدار تقریبی را به \( \Large 4^{\sqrt2} \) بدست آورید؟

حل ۴: می‌دانیم، \( \Large \sqrt2 \simeq 1.4 \) است. این عدد را روی محور \( \Large x \)ها پیدا کرده و به نمودار وصل می‌کنیم. بعد به محور \( \Large y \)ها وصل و عدد را می‌خوانیم.

1	۰	-1	x
4	1	\( \Large \frac{1}{4} \)	y

---

---

قرینه تابع نمایی :

تابع زیر را در نظر بگیرید:

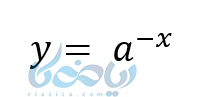
تابع بالا قرینه تابع زیر است:

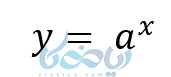
تابع اول را به صورت زیر نیز می‌توان نوشت:

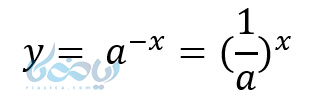
پس دو تابع زیر قرینه یکدیگر هستند:

نمودار این دو تابع بر اساس آموزش تابع نمایی نسبت به محور \( \Large y \) ها قرینه هم هستند.

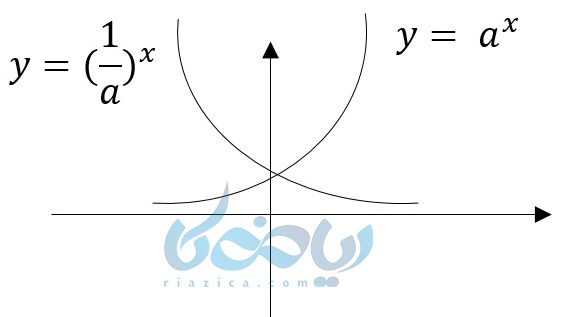
نکته مهم در آموزش تابع نمایی:

دو تابع زیر را در نظر بگیرید. این دو تابع نسبت به محور \( \Large x \)ها قرینه هستند.

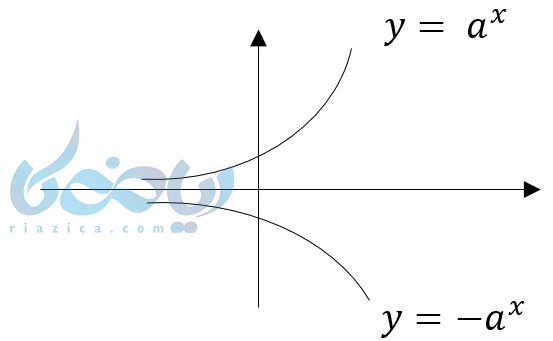
پس اگر \( \Large x \) قرینه شود، نمودار نسبت به محور \( \Large y \)ها قرینه می‌شود. ولی اگر \( \Large a^x \) قرینه شود نسبت به محور \( \Large x \) ها قرینه می شود.

نکته ۱: در مورد مقایسه دو عدد توان دار با پایه های برابر اگر پایه عدد بزرگتر از یک باشد، هرچه توان بیشتر باشد عدد بزرگتر است. چون در اصل نمودار توابع نمایی با پایه بزرگتر از یک، یک تابع صعودی است. یعنی هر چه \( \Large x \) ها بیشتر می‌شوند \( \Large y \)‌ها نیز بزرگتر می‌شوند.

ولی وقتی پایهٔ عددی بین صفر و یک است، نمودار یک نمودار نزولی خواهد بود. هرچه توان یا همان \( \Large x \) بیشتر می‌شود \( \Large y \)ها کوچکتر می‌شود. پس داریم:

\( \LARGE 4^{\sqrt5} > 4^{\sqrt3} \)

\( \LARGE (\frac{1}{2})^{\sqrt5} < (\frac{1}{2})^{\sqrt3} \)

نکته ۲: توابع نمایی، توابع یک به یک هستند. یعنی به ازای هر \( \Large x \) یک \( \Large y \) و به ازای هر \( \Large y \) یک \( \Large x \) داریم.

معادلات نمایی در تابع نمایی

معادلاتی که در آن متغیر یا مجهول در توان قرار گرفته باشد، معادله نمایی نامیده می‌شود. در آموزش تابع نمایی پی میبریم که برای حل معادلات نمایی از خاصیت یک به یک بودن آن ها استفاده می‌شود. به این صورت که اگر \( \Large a \) یک عدد حقیقی مثبت مخالف 1 باشد داشته باشیم.

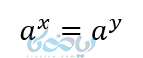
آنگاه

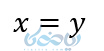
و برعکس.

برای حل معادلات نمایی هر دو طرف را به صورت عدد توان دار با پایه مساوی در می‌آوریم. سپس از خاصیت بالا استفاده کرده و معادله را حل می کنیم. به مثال‌های زیر توجه کنید که با کمک آموزش تابع نمایی حل شده است:

مثال ۵:

\( \Large 3^{3x-1} = 81 \)

\( \Large 3^{3x-1} = 3^4 \)

\( \Large 3x – 1 = 4 \)

\( \Large \rightarrow x = \frac{5}{3} \)

مثال ۶:

\( \Large 5^{x+3} = 125^{x-1} \)

\( \Large 5^{x+3} = (5^3)^{x-1} \)

\( \Large 5^{x+3} = 5^{3x-3} \)

\( \Large x +3 = 3x – 3 \)

\( \Large 6 = 2x \)

\( \Large \rightarrow x = 3 \)

مثال ۷:

 \( \Large (\frac{3}{5})^{x+2} = \frac{125}{27} \)

\( \Large (\frac{3}{5})^{x+2} = (\frac{3}{5})^{-3} \)

\( \Large x + 2 = -3 \)

\( \Large \rightarrow x = -5 \)

آخر کلاس: تابع نمایی، تابع موفقیت

به شکل زیر دقت کنید. این شکل یک تابع نمایی است. مجور افقی آن زمان و محور قائم آن موفقیت نام دارند. این نمودار می‌تواند مربوط به هر فردی در هر کجای این کره‌ی خاکی باشد و نشان‌دهنده‌ٔ موفقیت‌هایی که او در طول زمان بدست آورده.

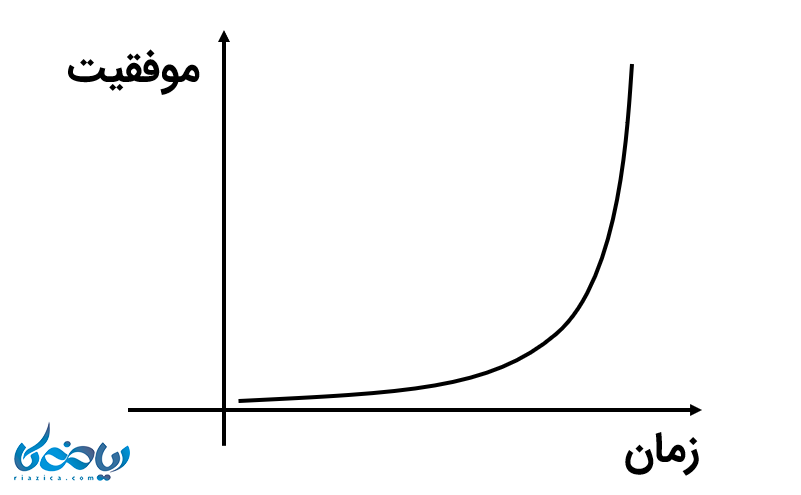
اجازه دهید منظور خودم را واضح‌تر بگویم. شما در طول زمان تلاش می‌کنید تا به اهدافی که تعیین کرده‌اید برسید. در ابتدا رشد شما و موفقیت‌های بدست آمده کوچک و ناچیز هستند. در ادامه و با گذشت زمان اثر و تجربه‌ٔ موفقیت‌ها و شکت‌های گذشته خود را نشان می‌دهند. تا جایی که بعد از گذشت مدتی رشد شما به صورت نمایی بالا می‌رود. در این بین تنها چیزی که تضمین می‌کند شما به اهداف خود دست پیدا می‌کنید، ثابت قدم بودن در تلاش است.

هدف ما در ریاضیکا رشد و توسعه شما در زندگی و درست است. در صورتی که هر سوالی از مبحث آموزش تابع نمایی داشتید می‌توانید با درج آن در قسمت دیدگاه‌ها در پایین همین صفحه، آن را مطرح کنید. کارشناسان ما پاسخ سوالات شما را خواهند داد.

---

---