آموزش ریاضی پایه دوازدهم تجربی
معادله دایره ریاضی دوازدهم تجربی 🔴⚽️ + مثال و تصویر
در این درسنامه، نحوهی نوشتن معادله دایره و صورت گستردهی آن را یاد خواهیمگرفت. علاوه بر این، اوضاع نسبی دایره و خط و همچنین اوضاع نسبی دو دایره را با یکدیگر بررسی خواهیمکرد.
دایره چیست؟
به مجموعه نقاطی از صفحه دایره میگوییم که دارای فاصلهی یکسان از یک نقطه هستند. به رسم با پرگار نگاه کنید. فاصلهی سوزن پرگار با میلهی دیگر آن در هنگام رسم ثابت است. پس در واقع در حال رسم نقاطی هستیم که از سوزن پرگار به یک فاصله هستند. این دقیقاً مطابق همان تعریفی است که ابتدا گفتیم.
فاصلهی دو نقطه
برای نوشتن معادله ی دایره نیاز است تا مروری بر تعریف فاصلهی دو نقطه داشته باشیم. شکل زیر را در نظر بگیرید.
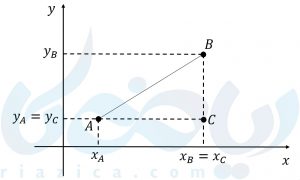
فکر کنید میخواهیم به صورت هندسی، فاصلهی دو نقطهی \( \Large A \) و \( \Large B\) را به دست آوریم. شما بودید چه کار میکردید؟ بله، کاملا درست است. از قضیهی فیثاغورث استفاده میکنیم. یعنی داریم:
\( \LARGE AB^2=AC^2+CB^2 \)
\( \LARGE AB=\sqrt{AC^2+CB^2} \)
مقدار \( \Large AC^2\) و \( \Large CB^2\)بر حسب مختصات نقاط \( \Large A\) و \( \Large B\) که در شکل بالا مشخص است برابر است با:
\( \LARGE AC^2=(x_C-x_A)^2 \)
\( \LARGE CB^2=(y_B-y_C)^2 \)
اگر به شکل بالا نگاه کنید، میبینید \( \Large x_C=x_B\) و \( \Large y_C=y_A\). پس معادلات بالا را به صورت زیر بازنویسی می کنیم:
\( \LARGE AC^2=(x_B-x_A)^2 \)
\( \LARGE CB^2=(y_B-y_A)^2 \)
بنابراین اندازه \( \Large AB\) که از ابتدا به دنبال آن بودیم برابر است با:
\( \Large \sqrt{(x_B-x_A)^2+(y_B-y_A)^2} \)
مثال 1: دو نقطهی \( \Large O=(2, 5)\) و \( \Large P=(-1, 9)\) را در صفحه داریم. فاصلهی این دو نقطه را محاسبه کنید.
حل: طبق معادلهی بالا، اندازهی \( \Large PO\) که همان فاصلهی آنهاست، برابر است با:
\( \Large \sqrt{(x_P-x_O)^2+(y_P-y_O)^2} \)
\( \Large =\sqrt{(-1-2)^2+(9-5)^2}\)
\( \Large =\sqrt{9+16}=\sqrt{25}=5 \)
معادله ی دایره
همانطور که گفتیم، دایره از مجموعهٔ نقاطی که از یک نقطهی ثابت به یک فاصلهاند تشکیل شده است. این نقطهی ثابت را مرکز دایره و فاصلهی این نقطه تا نقاط دیگر را شعاع مینامیم. بنابراین تمام اطلاعاتی که برای نوشتن معادله دایره نیاز داریم، مرکز و شعاع آن است. بیاید معادله ی دایره ای به مرکز \( \Large O(\alpha, \beta)\) و شعاع \( \Large r\) را بنویسیم. فاصلهی یک نقطه از دایره به مختصات \( \Large (x, y)\) از مرکز \( \Large O\) برابر است با:
\( \Large \sqrt{(x-\alpha)^2+(y-\beta)^2} \)
که این فاصله برابر است با شعاع دایره، یعنی همان \( \Large r\). پس معادلهی یک دایره به صورت زیر در میآید:
\( \Large r=\sqrt{(x-\alpha)^2+(y-\beta)^2} \)
\( \Large r^2=(x-\alpha)^2+(y-\beta)^2 \)
چند مثال مهم از معادله دایره
مثال 2: معادله دایره ای به مرکز \( \Large (5, -4)\) و شعاع 2 را بنویسید.
حل:
\( \Large 2^2=(x-5)^2+(y-(-4))^2 \)
\( \Large \Rightarrow 4=(x-5)^2+(y+4)^2 \)
مثال 3: اگر معادله دایره ای \( \Large 9=(x+2)^2+(y-1)^2 \) باشد، مرکز و شعاع آن را بیابید.
حل: به فرم معادلهی داده شده نگاه می کنیم. 9 همان \( \Large r^2\) است. پس \( \Large r\) یا همان شعاع برابر با 3 است. \( \Large (x+2)^2\) هم همان \( \Large x-(-2)\) است که در فرم اصلی، به صورت \( \Large (x-\alpha)^2\) نوشتیم. پس \( \Large \alpha=-2\). به همین ترتیب، \( \Large (y-1)^2\) نیز همان \( \Large (y-\beta)^2\) است، درنتیجه \( \Large \beta=1\). پس مرکز دایره برابر است با \( \Large O=(\alpha, \beta)=(-2, 1)\).
معادله دایره : معادله ی گسترده
منظور از معادله ی گسترده یا ضمنی دایره چیست؟ اگر معادله دایره را ساده کنیم، یعنی مراحل زیر را انجام دهیم، به معادله ی گسترده ی دایره میرسیم.
\( \Large r^2=(x-\alpha)^2+(y-\beta)^2 \)
\( \begin{align} \LARGE r^2& \LARGE =x^2-2 \alpha x+ \alpha^2 \\& \LARGE+y^2-2 \beta y+ \beta^2 \end {align} \)
\( \begin{align} \LARGE r^2& \LARGE =x^2+y^2-2 \alpha x \\& \LARGE-2 \beta y+\alpha^2+ \beta^2 \end {align} \)
اگر در عبارت بالا، \( \Large -2\alpha\) را \( \Large a\) بنامیم، \( \Large -2\beta\) را \( \Large b\) بنامیم، و \( \Large \alpha^2+\beta^2-r^2\) را \( \Large c\) بنامیم، صورت معادله، به شکل \( \Large x^2+y^2+ax+by+c=0\) در میآید. برای اینکه این معادله را به فرم غیر گسترده درآوریم، کافی است به صورت زیر، عبارات \( \Large (\frac{a}{2})^2\) و \( \Large (\frac{b}{2})^2\) را اضافه و کم کنیم تا دو مربع کامل ایجاد شود:
\( \Large (x^2+ax+(\frac{a}{2})^2)+ \)
\( \Large (y^2+by+(\frac{b}{2})^2) \)
\( \Large -(\frac{a}{2})^2-(\frac{b}{2})^2+c=0\)
اگر پرانتز اول را به صورت یک مربع کامل و پرانتز دوم را به صورت یک مربع کامل بنویسیم و سه جملهی آخر را نیز ساده کنیم، به معادلهی زیر می رسیم:
\( \LARGE (x+\frac{a}{2})^2+(y+\frac{b}{2})^2= \)
\( \LARGE \frac{a^2+b^2-4c}{4} \)
پس طبق رابطهی بالا، اگر معادله ی گسترده ی یک دایره \( \Large x^2+y^2+ax+by+c=0\) باشد، مرکز دایره \( \Large O=(-\frac{a}{2}, -\frac{b}{2})\) و شعاع آن \( \Large \sqrt{\frac{a^2+b^2-4c}{4}}\) است. از آنجاییکه شعاع باید عددی مثبت باشد، پس معادلهی \( \Large x^2+y^2+ax+by+c=0\) تنها زمانی نشان دهندهی یک دایره است که اولاً ضریب \( \Large x^2\) و \( \Large y^2\) با هم برابر باشد، ثانیا \( \Large \frac{a^2+b^2-4c}{4}>0\) باشد.
چند مثال از معادله ی گسترده
مثال 4: معادله ی گسترده ی دایرهای به صورت \( \Large x^2+y^2+6x+10y-2=0\) است. معادلهی غیرگستردهی دایره را بنویسید.
حل: کافی است جملات \( \Large x\) و \( \Large y\) را به صورت مربع کامل درآوریم. اعداد \( \Large 9\) و \( \Large 25\) را به صورتی که در زیر میبینید، اضافه و کم میکنیم:
\( \LARGE x^2+6x+9+ \)
\( \LARGE y^2+10y+25+ \)
\( \LARGE -9-25-2=0 \)
اگر سه جملهی اول معادلهی بالا را به صورت یک مربع کامل و سه جملهی بعدی را به صورت یک مربع کامل بنویسیم و سه جملهی آخر را نیز ساده کنیم، به معادلهی زیر می رسیم:
\( \Large (x+3)^2+(y+5)^2=36 \)
مثال 5: معادله ی گسترده ی دایرهای به صورت \( \Large x^2+y^2+4x+8y-2=0\) است. مرکز و شعاع آن را به دست آورید.
حل: ضریب \( \Large x\) که همان \( \Large a\) است، برابر با 4 و ضریب \( \Large y\) که همان \( \Large b\) است برابر با 8 است. پس مرکز دایره \( \Large O=(-\frac{4}{2}, -\frac{8}{2})=(-2, -4)\) است. شعاع دایره نیز طبق عبارتی که در بالا به دست آوردیم برابر است با:
\(\begin{align}\LARGE r&\LARGE=\sqrt{ \frac{a^2+b^2-4c}{4} }\\&\LARGE=\sqrt{\frac{4^2+8^2-4(-2)}{4}}\\&\LARGE=\sqrt{22}\end{align}\)
مثال 6: آیا معادلهی \( \Large 2x^2+2y^2+16x+4y=0\) معادلهی یک دایره است؟ اگر چنین است، مرکز و شعاع آن را به دست آورید.
حل: حواسمان باشد، در فرم گستردهای که معرفی کردیم، یعنی فرم \( \Large x^2+y^2+ax+by+c=0\) ضرایب \( \Large x^2\) و \( \Large y^2\) برابر 1 است. پس باید کل معادله را تقسیم بر 2 کنیم:
\( \Large x^2+y^2+8x+2y=0\)
\( \Large \Rightarrow a=8, b=2, c=0\)
\( \Large O=(-\frac{a}{2},-\frac{b}{2})\)
\( \Large \Rightarrow O=(-4,-1)\)
\( \LARGE r=\sqrt{\frac{a^2+b^2-4c}{4}}\)
\( \LARGE \Rightarrow r=\sqrt{\frac{64+4-0}{4}}=\Large\sqrt{17}\)
یک مفهوم مهم از درس معادله دایره : اوضاع نسبی خط و دایره
برای اینکه وضعیت نسبی یک خط و دایره را بررسی کنیم، نیاز داریم تا نحوهی محاسبهی فاصلهی یک نقطه از خط را یادآوری کنیم. همان طور که در درسنامهی آموزش معادله خط به زبان ساده خواندید، فاصلهی نقطهی \( \Large P(x_0, y_0)\) از خط به معادلهی \( \Large ax+by+c=0\) برابر است با:
\( \LARGE d=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\)
به طور کلی میتوان سه وضعیت برای یک خط و دایره تعریف کرد:
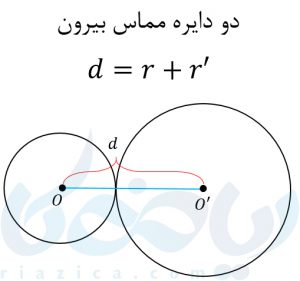
- اگر فاصلهی مرکز دایره از یک خط، برابر با شعاع باشد، آن خط بر دایره مماس است.
- اگر کمتر از شعاع باشد، دو شکل متقاطعاند.
- اگر بیشتر از شعاع باشد، یکدیگر را قطع نمیکنند.
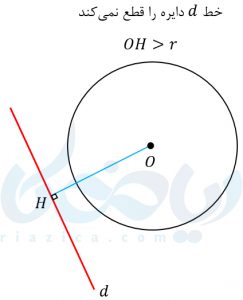
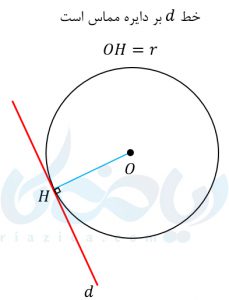
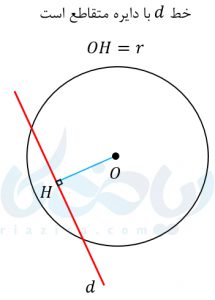
مثالهایی از اوضاع نسبی خط و دایره
مثال 7: وضعیت خط \( \Large 3x+4y=7\) و دایره \( \Large x^2+y^2+4x+6y+4=0\) را مشخص کنید.
حل: ابتدا باید مرکز و شعاع را به دست آوریم. سپس فاصلهی مرکز را تا خط داده شده حساب کرده و با مقایسهی آن با شعاع، وضعیت خط و دایره را تعیین کنیم.
\( \Large x^2+y^2+4x+6y+1=0\)
\( \LARGE \Rightarrow a=4, b=6\)
\( \LARGE O=(-\frac{a}{2}, -\frac{b}{2})\)
\( \LARGE \Rightarrow O=(-2, -3)\)
\( \LARGE r=\sqrt{\frac{a^2+b^2-4c}{4}}\)
\(\begin{align} \LARGE \Rightarrow r&\LARGE=\sqrt{\frac{16+36-16}{4}}\\&\LARGE=\sqrt{9}=3\end{align}\)
\( \LARGE d=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\)
\( \Large\Rightarrow d=\frac{|3\times(-2)+4\times(-3)+(-7)|}{\sqrt{3^2+4^2}}\)
\( \Large\Rightarrow d=\frac{25}{5}=5\)
از آنجاییکه \( \Large d\) بزرگتر از \( \Large r\) است، در نتیجه دایره و خط همدیگر را قطع نمی کنند.
مثال 8: معادله دایره ای را بنویسید که مرکز آن \( \Large O(-3, 4)\) بوده و بر خط \( \Large 5x-12y=2\) مماس باشد.
حل: همان طور که گفتیم زمانی دایره بر خط مماس است که فاصلهی مرکز آن از خط، برابر با شعاع باشد.
\( \LARGE d=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\)
\( \Large d=\frac{|5\times(-3)-12\times4+(-2)|}{\sqrt{5^2+(-12)^2}}\)
\( \LARGE d=\frac{65}{13}=5\)
\( \LARGE \Rightarrow r=d=5\)
حالا هم مرکز دایره را داریم، هم شعاع آن. کافی است معادله دایره را به فرم غیرگسترده بنویسیم:
\( \Large (x-\alpha)^2+(y-\beta)^2=r^2\)
\( \Large O=(-3,4), r=d=5\)
\( \Large \Rightarrow (x+3)^2+(y-4)^2=25\)
مثال مهم خط و دایرهی متقاطع
مثال 9: دایرهای داریم که مرکز آن نقطهی \( \Large O(15, 5)\) است. این دایره روی خط \( \Large 3x+4y=5\) وتری به طول 10 جدا میکند. معادلهی این دایره را بنویسید.
حل: به شکل زیر نگاه کنید.
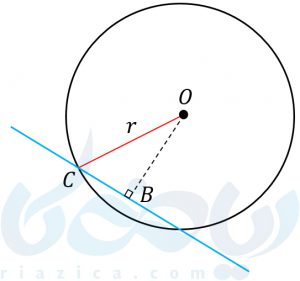
در مثلث \( \Large OBC\)، طول \( \Large BC\) برابر با نصف وتر، یعنی 5 است. ابتدا طول \( \Large OB\) که همان فاصلهی مرکز دایره از خط است را به دست میآوریم. سپس شعاع دایره که همان \( \Large OC\) است را طبق قضیهی فیثاغورث محاسبه میکنیم:
\( \LARGE OB=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\)
\( \Large OB=\frac{|3\times15+4\times5-5|}{\sqrt{3^2+4^2}}\)
\( \LARGE OB=\frac{60}{5}=12\)
\(\begin{align} \Large r=OC&\Large=\sqrt{OB^2+BC^2}\\&\Large=\sqrt{12^2+5^2}\\&\Large=13\end{align}\)
بنابراین با در نظر داشتن مرکز دایره که \( \Large O(15, 5)\) است و شعاع آن که برابر با 13 است، معادله به شکل زیر در میآید:
\( \Large (x-15)^2+(y-5)^2=13^2\)
آموزش معادله دایره : اوضاع نسبی دو دایره
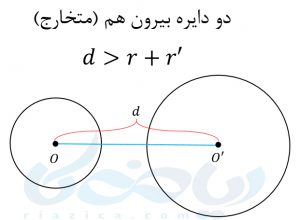
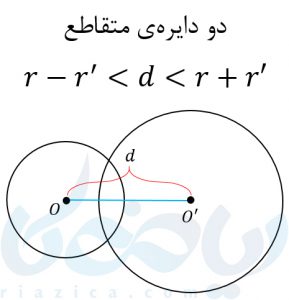
یک دایره با مرکز \( \Large O\) و شعاع \( \Large r\) و دایرهی دیگر با مرکز \( \Large O’\) و شعاع \( \Large r’\) داریم. پارهخطی که این دو مرکز را به هم وصل میکند، خط المرکزین نامیده میشود. بر اساس اندازهی خط المرکزین و همچنین اندازهی شعاع دو دایره، یکی از حالتهای زیر اتفاق میافتد:

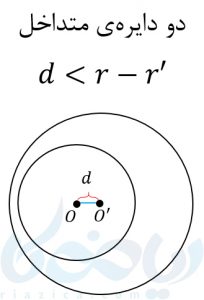
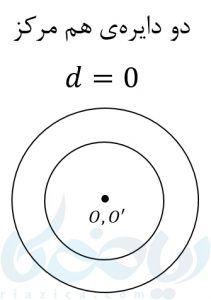
مثال 10: وضعیت دو دایره با معادلات زیر را مشخص کنید.
1) \( \Large x^2+y^2+8x+4y+4=0\)
2) \( \Large x^2+y^2+2x-4y-4=0\)
حل: مرکز دایرهی 1 را \( \Large O_1\) و مرکز دایرهی 2 را \( \Large O_2\) مینامیم. ابتدا مختصات مراکز و شعاعها را محاسبه کرده و اندازهی خط المرکزین \( \Large O_1O_2\) را به دست میآوریم. سپس اندازهی \( \Large r_1+r_2\) و \( \Large r_1-r_2\) را محاسبه می کنیم. با مقایسهی این دو مقدار و اندازهی خط المرکزین، وضعیت دو دایره را تعیین می کنیم:
\(\begin{align} \LARGE O_1&\LARGE=(-\frac{a_1}{2},-\frac{b_1}{2})\\&\LARGE=(-4, -2)\end{align}\)
\( \begin{align}\LARGE O_2&\LARGE=(-\frac{a_2}{2},-\frac{b_2}{2})\\&\LARGE=(-1, 2)\end{align}\)
\( \Large r_1=\sqrt{\frac{64+16-16}{4}}=4\)
\( \Large r_2=\sqrt{\frac{4+16+16}{4}}=3\)
طول \( \Large O_1O_2\) که همان خط المرکزین است برابر است با:
\( \Large \sqrt{(-1+4)^2+(2+2)^2}\)
\( \Large \Rightarrow d=O_1O_2=5\)
از آنجاییکه \( \Large r_1-r_2<d<r_1+r_2\) است، پس متقاطع هستند.
مثال 11: دو معادله دایره به صورت زیر داری. وضعیت دایره نسبت به هم را مشخص کنید.
1) \( \Large x^2+y^2-4x-6y-3=0\)
2) \( \Large x^2+y^2+6x+18y+65=0\)
حل: مرکز اولی را \( \Large O_1\) و مرکز دومی را \( \Large O_2\) مینامیم. ابتدا مختصات مراکز و شعاعها را محاسبه کرده و اندازهی خط المرکزین \( \Large O_1O_2\) را به دست میآوریم. سپس اندازهی \( \Large r_1+r_2\) و \( \Large r_1-r_2\) را محاسبه می کنیم. با مقایسهی این دو مقدار و اندازهی خط المرکزین، وضعیت دو دایره را تعیین می کنیم:
\(\begin{align} \LARGE O_1&\LARGE=(-\frac{a_1}{2},-\frac{b_1}{2})\\&\LARGE=(2, 3)\end{align}\)
\( \begin{align}\LARGE O_2&\LARGE=(-\frac{a_2}{2},-\frac{b_2}{2})\\&\LARGE=(-3, -9)\end{align}\)
\( \Large r_1=\sqrt{\frac{16+36+12}{4}}=4\)
\( \Large r_2=\sqrt{\frac{36+324-260}{4}}=5\)
طول \( \Large O_1O_2\) که همان خط المرکزین است برابر است با:
\( \Large \sqrt{(2+3)^2+(3+9)^2}\)
\( \Large \Rightarrow d=O_1O_2=13\)
از آنجاییکه \( \Large d>r_1+r_2\) است، پس متخارج هستند.
توصیه میشه قبل از خواندن این پست ،پست مقاطع مخروطی را مطالعه کنید.
زنگ آخر آموزش معادله دایره
در این درسنامه یاد گرفتیم که چگونه به راحتی معادله دایره و صورت گسترده ی آن را بنویسیم. همچنین وضعیت نسبی یک دایره و خط و وضعیت نسبی دو دایره را، هم با شکل، هم با نوشتن معادله و هم با چند مثال زیبا بررسی کردیم. با تسلط بر مفاهیم این درسنامه و حل مثالها، هیچ مشکلی در این مبحث نخواهیم داشت.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث دایره دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





مختصر و مفید بود .دمین ایسی یاشا