مجانب افقی و مجانب قائم ✏️⚛️ – راحت پیدا کن!

در درسنامهٔ مجانب افقی و مجانب قائم به بررسی مجانب‌های تابع می‌پردازیم. سعی می‌کنیم با توضیح ساده و حل مثال‌های مختلف از کتاب حسابان 2 به درک بهتر شما از این مبحث کمک کنیم. در صورتی که احساس می‌کنید نیاز به مرور مباحث گذشته دارید، می‌توانید قبل از شروع مطالعهٔ این درسنامه، درسنامه‌های حد بی نهایت و حد در بی نهایت را مطالعه کنید. مجانب افقی با حد در بی نهایت و مجانب عمودی با حد بی نهایت مرتبط است.

مجانب افقی

به شکل زیر نگاه کنید:

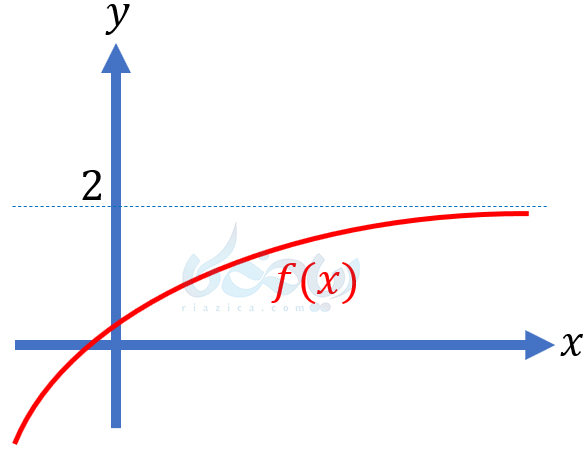
همان طور که می‌بینید، وقتی که \(\Large x\) به \(\Large +\infty\) میل می‌کند، \(\Large f(X)\) به \(\Large 2\) میل می‌کند. به بیان ساده‌تر، نمودار تابع به خط \(\Large y=2\) نزدیک می‌شود. در این حالت می‌گوییم خط \(\Large y=2\) مجانب افقی تابع \(\Large f\) است. 

حال به شکل زیر نگاه کنید:

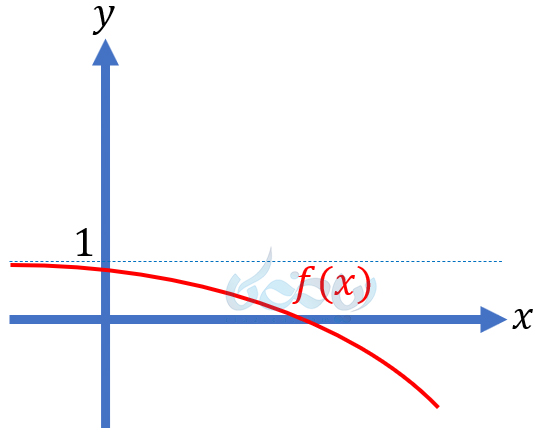
در شکل بالا، زمانی که \(\Large x\) به \(\Large -\infty\) میل می‌کند، \(\Large f(x)\) به \(\Large 1\) میل می‌کند. به بیان ساده‌تر، نمودار تابع به خط \(\Large y=1\) نزدیک می‌شود. در این حالت نیز می‌گوییم خط \(\Large y=1\) مجانب افقی تابع \(\Large f\) است. 

بنابراین می‌توانیم اینگونه جمع‌بندی کنیم:

دقت کنید که لازم نیست هر دو حالت بالا برقرار باشد؛ به عبارت دیگر، اگر تنها یکی از شروط \(\Large\lim\limits_{x \to +\infty}f(x)=L\) یا \(\Large \lim\limits_{x \to -\infty}f(x)=L\) برقرار باشد، می‌گوییم خط \(\Large y=L\) مجانب افقی تابع \(\Large y=f(x)\) است.

مثال از درسنامهٔ مجانب افقی و مجانب قائم

مثال 1: مجانب‌های افقی تابع \(\Large f(x)=\frac{x}{2x^2+4x-1}\) را به دست آورید.

حل: کافی است حدهای \(\Large \lim\limits_{x \to +\infty}f(x)\) و \(\Large \lim\limits_{x \to -\infty}f(x)\) را محاسبه کنیم. از آنجاییکه درجهٔ مخرج از صورت بیشتر است، حاصل هر دو حد برابر با صفر می‌شود. یعنی داریم:

\(\LARGE \lim\limits_{x \to +\infty}f(x)= \lim\limits_{x \to -\infty}f(x)=0\)

بنابراین، خط \(\Large y=0\) مجانب افقی تابع \(\Large f(x)\) است.

مثال از درسنامهٔ مجانب افقی و مجانب قائم

مثال 2: مجانب‌های افقی تابع \(\Large f(x)=2+\frac{3x^2-1}{x^2+4x}\) را به دست آورید.

حل: مانند مثال قبل، کافی است حدهای \(\Large \lim\limits_{x \to +\infty}f(x)\) و \(\Large \lim\limits_{x \to -\infty}f(x)\) را محاسبه کنیم. با توجه به آنچه در درسنامهٔ حد در بی نهایت خواندیم، داریم:

\(\LARGE \lim\limits_{x \to \pm \infty}f(x)=\lim\limits_{x \to \pm \infty}(2+\frac{3x^2-1}{x^2+4x})\)

\(\LARGE =2+\lim\limits_{x \to \pm \infty}\frac{3x^2-1}{x^2+4x}\)

\(\LARGE =2+3\)

\(\LARGE =5\)

بنابراین، خط \(\Large y=5\) مجانب افقی تابع \(\Large f(x)\) است.

مجانب قائم

به شکل زیر نگاه کنید:

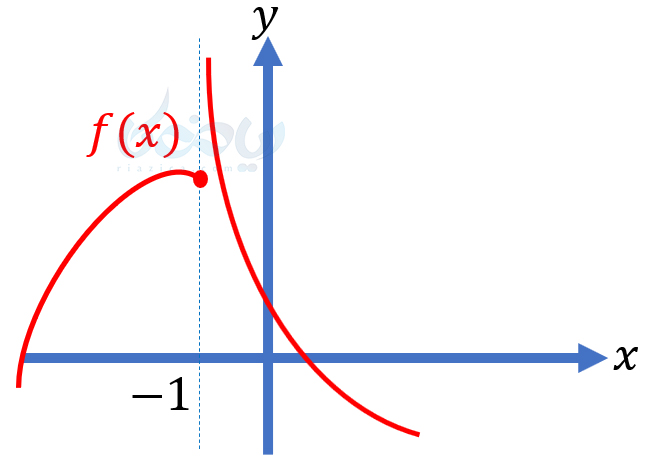
همان طور که می‌بینید، وقتی که \(\Large x\) از راست به \(\Large -1\) میل می‌کند، \(\Large f(x)\) به \(\Large +\infty\) میل می‌کند. به بیان ساده‌تر، نمودار تابع به خط \(\Large x=-1\) نزدیک می‌شود. در این حالت می‌گوییم خط \(\Large x=-1\) مجانب قائم تابع \(\Large f\) است. 

حال به شکل زیر نگاه کنید:

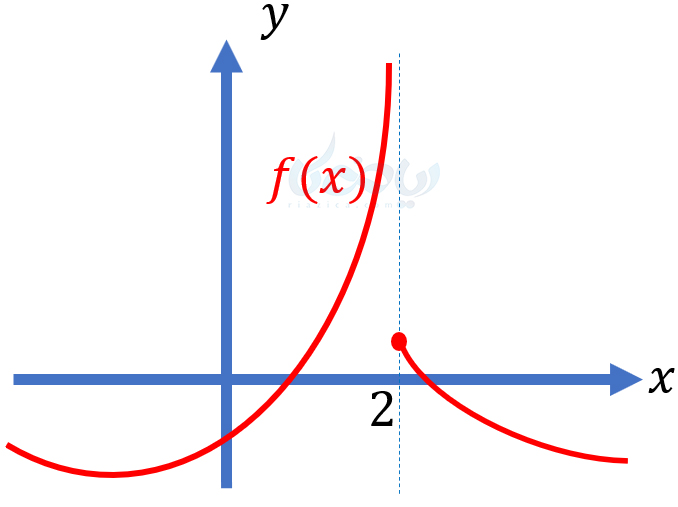
این بار زمانی که \(\Large x\) از چپ به \(\Large 2\) میل می‌کند، \(\Large f(x)\) به \(\Large +\infty\) میل می‌کند. به بیان ساده‌تر، نمودار تابع به خط \(\Large x=2\) نزدیک می‌شود. در این حالت نیز می‌گوییم خط \(\Large x=2\) مجانب قائم تابع \(\Large f\) است. 

دو حالت بالا می‌توانند به صورت مشابه برای \(\Large -\infty\) نیز رخ دهند. مثلاً به شکل زیر نگاه کنید:

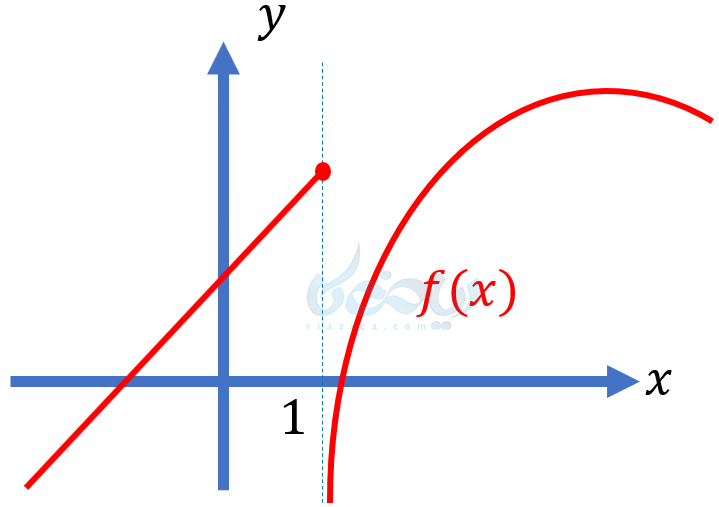
همان طور که در شکل بالا می‌بینید، وقتی که \(\Large x\) از راست به \(\Large 1\) میل می‌کند، \(\Large f(x)\) به \(\Large -\infty\) میل می‌کند. به بیان ساده‌تر، نمودار تابع به خط \(\Large x=1\) نزدیک می‌شود. در این حالت می‌گوییم خط \(\Large x=1\) مجانب قائم تابع \(\Large f\) است. 

 در شکل زیر نیز، زمانی که \(\Large x\) از چپ به \(\Large 3\) میل می‌کند، \(\Large f(X)\) به \(\Large -\infty\) میل می‌کند. به بیان ساده‌تر، نمودار تابع به خط \(\Large x=3\) نزدیک می‌شود. در این حالت نیز می‌گوییم خط \(\Large x=3\) مجانب قائم تابع \(\Large f\) است. 

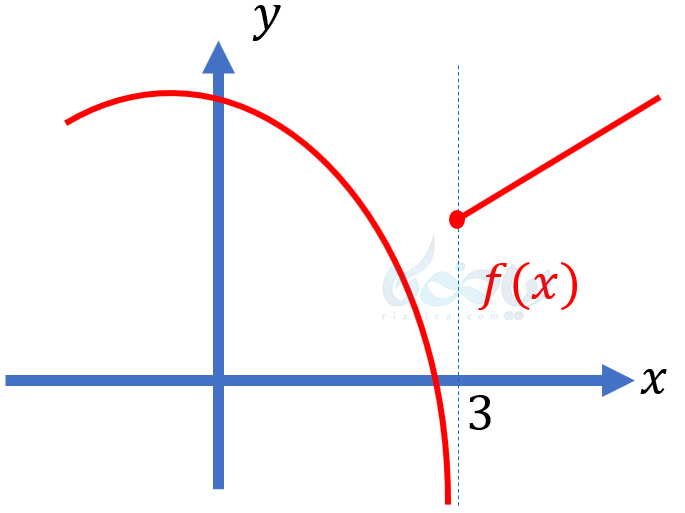
بنابراین می‌توانیم اینگونه جمع‌بندی کنیم:

دقت کنید که باز هم لازم نیست هر چهار حالت بالا برقرار باشد؛ اگر تنها یکی از شروط بالا برقرار باشد، می‌گوییم خط \(\Large x=a\) مجانب قائم تابع \(\Large y=f(x)\) است.

نکته: همان طور که در مثال‌های بعدی خواهید دید، برای یافتن مجانب‌های قائم توابع گویا (توابعی به صورت یک کسر که صورت و مخرج آن چندجمله‌ای است)، معمولاً باید به ریشه‌های مخرج آن توجه کرد.

مثال از درسنامهٔ مجانب افقی و مجانب قائم

مثال 3: آیا خط \(\Large x=2\) مجانب قائم تابع \(\Large f(x)=\frac{x^2+2x-8}{x^2-3x+2}\) است؟

حل: کافی است \(\Large \lim\limits_{x \to 2}f(x)\) را محاسبه کنیم. اگر حاصل برابر با \(\Large +\infty\) یا \(\Large -\infty\) شد، خط \(\Large x=2\) مجانب قائم تابع خواهد بود. بنابراین داریم:

\(\LARGE \lim\limits_{x \to 2}f(x)=\lim\limits_{x \to 2}\frac{x^2+2x-8}{x^2-3x+2}\)

صورت و مخرج کسر بالا را به صورت زیر تجزیه می‌کنیم (در صورتی که تجزیهٔ عبارت‌های جبری را فراموش کرده‌اید، درسنامهٔ تجزیهٔ عبارت‌های جبری به 4 روش مختلف را مرور کنید):

\(\LARGE \lim\limits_{x \to 2}\frac{(x-2)(x+4)}{(x-2)(x-1)}\)

هم در صورت و هم در مخرج، عبارت \(\Large x-2\) وجود دارد. پس آن را ساده می‌کنیم. بنابراین حد به صورت زیر در می‌آید:

\(\LARGE \lim\limits_{x \to 2}\frac{x+4}{x-1}\)

حال می‌توانیم عدد \(\Large 2\) را در صورت و مخرج کسر جاگذاری کنیم:

\(\LARGE \lim\limits_{x \to 2}\frac{x+4}{x-1}=\frac{6}{1}=6\)

بنابراین، خط \(\Large x=2\) مجانب قائم تابع \(\Large f(x)\) نیست.

مثال از درسنامهٔ مجانب افقی و مجانب قائم

مثال 4: آیا خط \(\Large x=-3\) مجانب قائم تابع \(\Large f(x)=\frac{x^2-4x+3}{x^2+5x+6}\) است؟

حل: مانند مثال قبل، کافی است \(\Large \lim\limits_{x \to -3}f(x)\) را محاسبه کنیم. اگر حاصل برابر با \(\Large +\infty\) یا \(\Large -\infty\) شد، خط \(\Large x=-3\) مجانب قائم تابع خواهد بود. بنابراین داریم:

\(\LARGE \lim\limits_{x \to -3}f(x)=\lim\limits_{x \to -3}\frac{x^2-4x+3}{x^2+5x+6}\)

صورت و مخرج کسر بالا را به صورت زیر تجزیه می‌کنیم:

\(\LARGE \lim\limits_{x \to -3}\frac{(x-3)(x-1)}{(x+2)(x+3)}\)

اگر در کسر بالا، \(\Large x\) به سمت \(\Large -3\) میل کند، مخرج به سمت صفر میل خواهد کرد و در نتیجه، حاصل کسر، مثبت یا منفی بی‌نهایت خواهد شد. بنابراین حاصل حد برابر با \(\Large +\infty\) یا \(\Large -\infty\) خواهد شد. پس تا همین جا جواب مثال را یافته‌ایم. خط \(\Large x=-3\) مجانب قائم تابع است. اما بیایید ببینیم کدام یک از حالت‌های \(\Large +\infty\) یا \(\Large -\infty\) اتفاق می‌افتد. ابتدا باید تابع \(\Large f(x)=\frac{(x-3)(x-1)}{(x+2)(x+3)}\) را تعیین علامت کنیم:

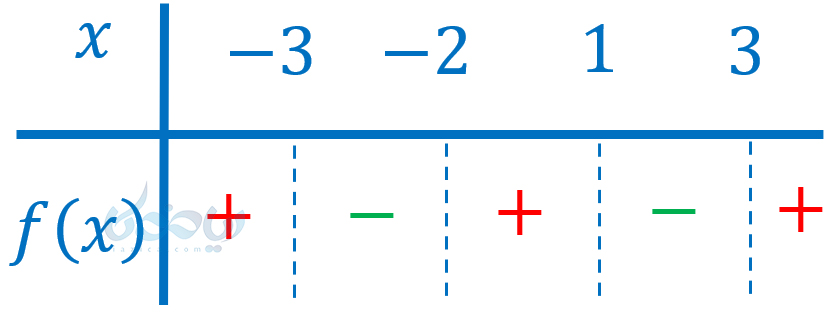
باتوجه به جدول تعیین علامتی بالا، اگر از راست به \(\Large x=-3\) نزدیک شویم، حاصل حد برابر با \(\Large -\infty\) خواهد؛ اگر از چپ به \(\Large x=-3\) نزدیک شویم، حاصل حد برابر با \(\Large +\infty\) خواهد شد. یعنی داریم:

\(\LARGE  \lim\limits_{x \to -3^+}f(x)=-\infty\)

\(\LARGE  \lim\limits_{x \to -3^-}f(x)=+\infty\)

مثال از درسنامهٔ مجانب افقی و مجانب قائم

مثال 5: با توجه به آنچه در مورد مجانب‌های افقی و قائم نمودار تابع خوانده‌اید، یک نمودار کلی برای تابع \(\Large \frac{x^2-2x-3}{x^2+x-2}\) رسم کنید.

حل: سوال بالا، سوال ریاضی نیست! چون عبارت “نمودار کلی” در ریاضی فاقد معنی است. اما عامدانه این مثال را به این صورت مطرح کرده‌ایم تا سعی کنید برای یک تابع با توجه به مجانب‌های آن، یک نمودار تقریبی رسم کنید. بیایید با هم این کار را انجام دهیم.

ابتدا رفتار تابع در \(\Large+\infty\) و \(\Large -\infty\) بررسی می‌کنیم. به عبارت دیگر، مجانب‌های افقی تابع را به دست می‌آوریم. داریم:

\(\LARGE  \lim\limits_{x \to +\infty} \frac{x^2-2x-3}{x^2+x-2}=1\)

\(\LARGE  \lim\limits_{x \to -\infty} \frac{x^2-2x-3}{x^2+x-2}=1\)

بنابراین خط \(\Large y=1\) مجانب افقی تابع است. حالا سراغ مجانب‌های قائم تابع می‌رویم. ابتدا کسر \(\Large \frac{x^2-2x-3}{x^2+x-2}\) را به صورت زیر تجزیه می‌کنیم:

\(\LARGE  f(x)= \frac{x^2-2x-3}{x^2+x-2}= \frac{(x+1)(x-3)}{(x+2)(x-1)}\)

مقدار تابع در ریشه‌های مخرج، نامتناهی می‌شود. بنابراین باید حد چپ و راست تابع، زمانی که \(\Large x\) به \(\Large 1\) و \(\Large -2\) میل می‌کند را بررسی کنیم.برای این کار، ابتدا باید تابع \(\Large f(x)=\frac{(x+1)(x-3)}{(x+2)(x-1)}\) را تعیین علامت کنیم:

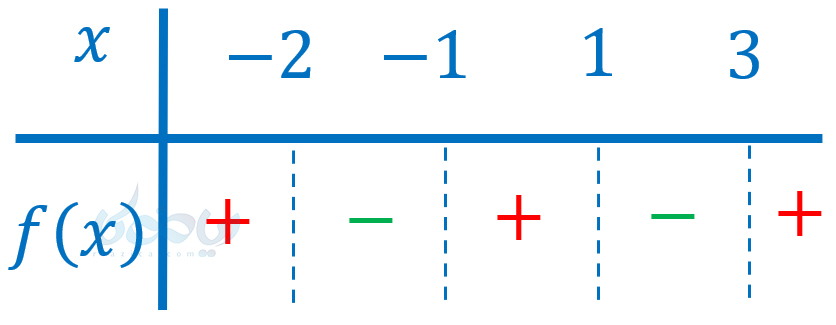
بنابراین حدود زیر به دست می‌آیند:

\(\LARGE  \lim\limits_{x \to -2^+}f(x)=-\infty\)

\(\LARGE  \lim\limits_{x \to -2^-}f(x)=+\infty\)

\(\LARGE  \lim\limits_{x \to 1^+}f(x)=-\infty\)

\(\LARGE  \lim\limits_{x \to 1^-}f(x)=+\infty\)

پس با توجه به مجانب‌های تابع، احتمالاً نمودار آن به صورت زیر خواهد بود:

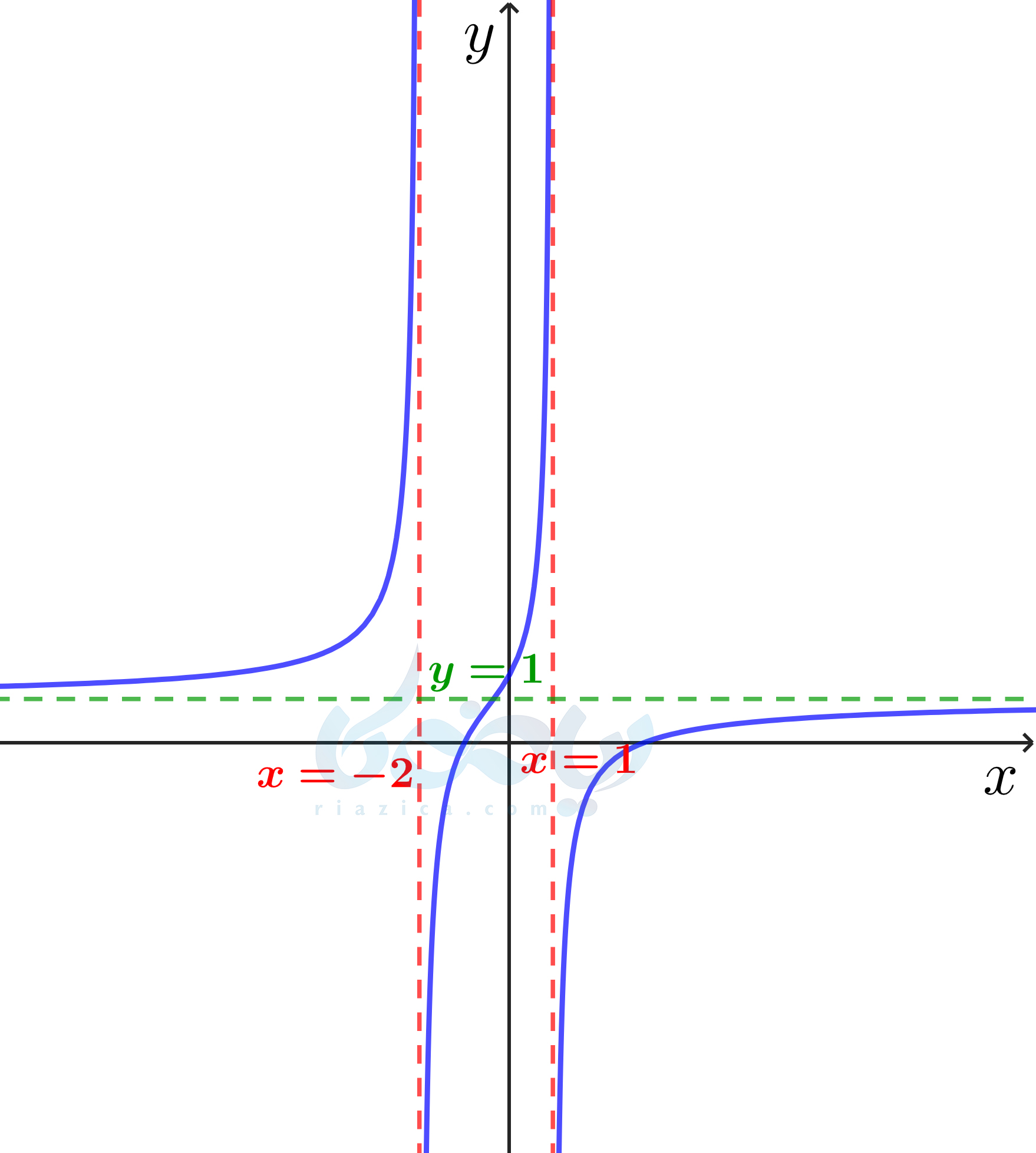
اگرچه نمودار دقیق تابع نیز، دقیقاً مانند شکلی است که در بالا رسم کرده‌ایم، اما ممکن است برای توابع دیگر چنین اتفاقی نیفتد. مثلاً ما بررسی نکردیم که تابع در مجانب‌های افقی به چه صورتی به آن نزدیک می‌شود؛ از بالا به آن نزدیک می‌شود، از پایین به آن نزدیک می‌شود و یا به صورت نوسانی به آن نزدیک می‌شود. یا مثلاً مینیمم‌ها و ماکزیمم‌های تابع را به دست نیاوردیم. همچنین، در مورد صفرهای تابع نیز دقتی نکردیم. اما با توجه به آنچه که برای مجانب‌های تابع به دست آوردیم، می‌توانیم به صورت غیر دقیق بگوییم نمودار رسم شده با نمودار تابع مشابه است.

زنگ آخر درسنامهٔ مجانب افقی و مجانب قائم

در درسنامه‌ای که از حسابان 2 خواندیم، مجانب افقی و مجانب قائم تابع را بررسی کرده و مثال هایی از فصل سوم کتاب حسابان 2 حل کردیم.

ما در ریاضیکا آماده‌ی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با درسنامهٔ مجانب افقی و مجانب قائم دارید، در دیدگاه‌ها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند ‌داد.