عبارت های جبری نهم 🅰️⚜️ – دنبال جملات متشابه باش!

در درسنامۀ عبارت های جبری نهم ابتدا عبارت های یک جمله ای را معرفی می‌کنیم. سپس، درجۀ یک جمله ای نسبت به متغیر را بررسی کرده و بر اساس آن جملات متشابه را معرف می‌کنیم. در انتها نیز به چند جمله ای ها می‌پردازیم. سعی می‌کنیم با حل مثال، در درک بهتر این مبحث به شما کمک کنیم. به قسمت اول از درسنامۀ عبارت های جبری نهم توجه کنید.

عبارت یک جمله ای

به عبارت‌هایی که از حاصل ضرب یک عدد حقیقی در توان‌های صحیح و نامنفی یک یا چند متغیر تشکیل شده‌اند، یک جمله ‌ای می‌گوییم. به طور مثال هر یک از عبارت‌های زیر، یک جمله ‌ای هستند:

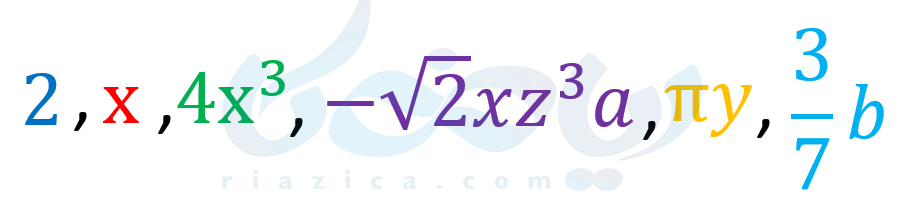
اما عبارت‌های زیر یک جمله ای نیستند:

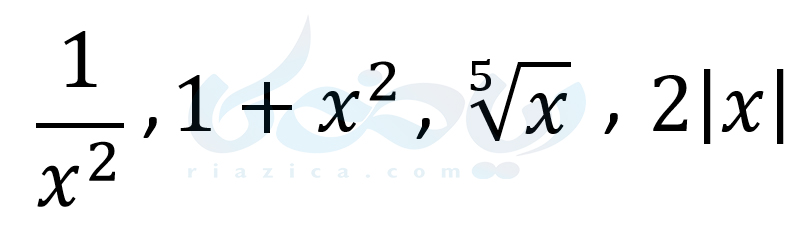
زیرا در عبارت \(\Large \frac{1}{x^2}\)، توان \(\Large x\) منفی است. در نتیجه یک جمله ای نیست. عبارت \(\Large 1+x^2\) از جمع دو یک جمله‌ای \(\Large 1\) و \(\Large x^2\) تشکیل شده است و خودش یک جمله‌ای نیست. توان عبارت \(\Large \sqrt[5]{x}\) صحیح نیست (توان این عبارت کسری است و در آینده با آن آشنا می‌شوید). در نتیجه این عبارت هم یک جمله ای نیست. عبارت \(\Large 2|x|\) نیز شامل قدر مطلق است که در شرط ما برای یک جمله ای بودن نمی گنجد. به قسمت بعدی از درسنامۀ عبارت های جبری نهم توجه کنید.

درجه نسبت به متغیر

توان یک ،یک جمله ای نسبت به یک متغیر را درجۀ آن یک جمله‌ای نسبت به متغیر مورد نظر می‌گوییم. مثلاً در عبارت \(\Large 4x^3y^2z^5\)، توان \(\Large x\) برابر است با \(\Large 3\). بنابراین می‌گوییم درجۀ یک جمله‌ای \(\Large 4x^3y^2z^5\) نسبت به \(\Large x\) برابر است با \(\Large 3\). درجۀ همین یک جمله ای نسبت به متغیر \(\Large y\) برابر است با \(\Large 2\). درجۀ یک یک جمله ای نسبت به چند متغیر برابر است با مجموع درجات آن یک جمله‌ای نسبت به متغیرهای مورد نظر. مثلاً در یک جمله‌ای \(\Large 4x^3y^2z^5\)، درجۀ \(\Large 4x^3y^2z^5\) نسبت به دو متغیر \(\Large x\) و \(\Large y\) برابر است با مجموع درجۀ \(\Large 4x^3y^2z^5\) نسبت به متغیر \(\Large x\) و درجۀ \(\Large 4x^3y^2z^5\) نسبت به متغیر \(\Large y\). بابراین درجۀ \(\Large 4x^3y^2z^5\) نسبت به دو متغیر \(\Large x\) و \(\Large y\) برابر است با \(\Large 3+2=5\). در جدول زیر، درجات چند یک جمله‌ای را نسبت به چند متغیر به دست آورده‌ایم:

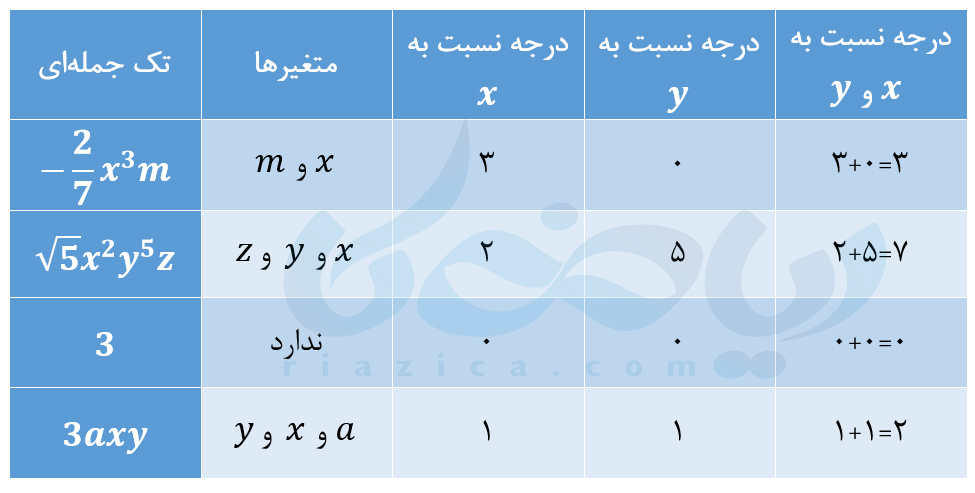
به قسمت بعدی از درسنامۀ عبارت های جبری نهم توجه کنید.

یک جمله ای های متشابه

یک جمله ‌ای‌هایی که قسمت متغیر آن‌ها یکسان است، با یکدیگر متشابه هستند. منظور از یکسان بودن قسمت متغیر این است که درجۀ هر یک جمله ای نسبت به تمام متغیرهایش با درجۀ یک جمله‌ای دیگر نسبت به متغیرهایش، نظیر به نظیر برابر باشد. به بیان خیلی ساده تر، باید دو مورد زیر برقرار باشد:

1. هر متغیری که در عبارت اول وجود دارد، در عبارت دوم نیز وجود داشته باشد.
2. توان هر متغیر در عبارت اول، برابر با توان متغیر در عبارت دوم باشد.

مثلاً دو یک جمله ‌ای \(\Large -\sqrt{2} x^2y^5z^3\) و \(\Large \frac{3}{5} x^2y^5z^3\) متشابه هستند. زیرا در هر دو، متغیرهای \(\Large x\) و \(\Large y\) و \(\Large z\) وجود دارد. توان متغیر \(\Large x\) در هر دو عبارت برابر با \(\Large 2\)، توان متغیر \(\Large y\) در هر دو عبارت برابر با \(\Large 5\) و توان متغیر \(\Large z\) در هر دو عبارت برابر با \(\Large 3\) است.

اما دو یک جمله ‌ای \(\Large  x^3\) و \(\Large 2 x^2\) متشابه نیستند. زیرا اگرچه در هر دو، متغیر \(\Large  x\) وجود دارد، اما توان متغیر \(\Large  x\) در هر دو عبارت یکی نیست. یا مثلاً دو یک جمله ‌ای \(\Large 3 x^5y\) و \(\Large \sqrt{7} x^5\) متشابه نیستند. زیرا متغیر \(\Large y\) در یک جمله ای اول وجود دارد، اما در یک جمله ای دوم وجود ندارد. به یک جمله ای هایی که متشابه نیستند، یک جمله ای های غیر متشابه می‌گوییم. به قسمت بعدی از درسنامۀ عبارت های جبری نهم توجه کنید.

چند جمله ای ها

اگر تعدادی یک جمله ای را با یکدیگر جمع و یا از یکدیگر تفریق کنیم، چند جمله ای به وجود می‌آید. مثلاً عبارت \(\Large x^2y^4z+x^3\) یک چند جمله ای است؛ زیرا از مجموع دو یک جمله ای \(\Large x^2y^4z\) و \(\Large x^3\) به وجود آمده است. برای جمع و تفریق تعدادی یک جمله ای باید عبارت‌های متشابه را با یکدیگر جمع و یا از یکدیگر تفریق کنیم. یعنی قسمت متغیر عبارت‌های متشابه را بدون تغییر گذاشته و ضرایب را جمع یا تفریق ‌کنیم. معمولاً چند جمله ای ها را نسبت به توان‌های نزولی یکی از متغیرها مرتب می‌کنیم. یعنی یک جمله ای هایی که شامل آن متغیر هستند و توان بزرگتری دارند را اول نوشته و یک جمله ای هایی که توان کوچکتری از آن متغیر را دارند، آخر می‌نویسیم. برای اینکه بهتر متوجه شوید، به مثال‌ بعدی از درسنامۀ عبارت های جبری نهم توجه کنید.

مثال از درسنامۀ عبارت های جبری نهم 

مثال 1: عبارت زیر  را ساده کرده و نسبت به توان‌های نزولی \(\Large y\) مرتب کنید.

\( 3z^2+4axy-2y^5-(2axy-y^5+2z^2)\)

حل: ابتدا علامت منفی پشت پرانتز را تاثیر می‌دهیم تا عبارت داده شده، به صورت زیر درآید:

\(3z^2+4axy-2y^5-2axy+y^5-2z^2\)

همان طور که گفتیم، ضرایب یک جمله ای های متشابه را با هم جمع و یا از هم کم می‌کنیم. یک جمله ای \(\Large 3z^2\) با \(\Large -2z^2\) متشابه است، یک جمله ای \(\Large 4axy\) با \(\Large -2axy\) متشابه است و یک جمله ای \(\Large -2y^5\) با \(\Large y^5\) متشابه است. در صورتی که ضرایب یک جمله ای های متشابه را جمع کنیم، عبارت زیر به دست می‌آید:

\(\LARGE z^2+2axy-y^5\)

در قسمت پایانی این مثال از درسنامۀ عبارت های جبری نهم باید چندجمله ای بالا را نسبت به توان‌های نزولی \(\Large y\) مرتب کنیم. همان‌طور که گفتیم، باید ببینیم در کدام یک جمله ای، متغیر \(\Large y\) بیشترین توان را دارد. آن را اول نوشته و سپس بقیۀ یک جمله ای ها را از توان بزرگ \(\Large y\) به توان کوچک \(\Large y\) بنویسیم. در یک جمله ای \(\Large -y^5\) ، توان \(\Large y\) برابر با \(\Large 5\) است. در یک جمله ای \(\Large 2axy\)، توان \(\Large y\) برابر با \(\Large 1\) است و در یک جمله ای \(\Large z^2\)، توان \(\Large y\) برابر با \(\Large 0\) است. بنابراین ابتدا \(\Large -y^5\) را نوشته، سپس \(\Large 2axy\) و در آخر \(\Large z^2\) را می‌نویسیم:

\(\LARGE -y^5+2axy+z^2\)

به مثال بعدی از درسنامۀ عبارت های جبری نهم توجه کنید.

مثال دیگری از عبارت های جبری نهم

مثال 2: عبارت زیر  را ساده کرده و نسبت به توان‌های نزولی \(\Large y\) مرتب کنید.

\( -(2x^3mn-4xy^2m)+xy^2m+5x^3mn\)

حل: ابتدا علامت منفی پشت پرانتز را تاثیر می‌دهیم تا عبارت داده شده، به صورت زیر درآید:

\(-2x^3mn+4xy^2m+xy^2m+5x^3mn\)

همان طور که گفتیم، ضرایب یک جمله ای های متشابه را با هم جمع و یا از هم کم می‌کنیم. یک جمله ای \(\Large -2x^3mn\) با \(\Large 5x^3mn\) متشابه است. یک جمله ای \(\Large 4xy^2m\) با \(\Large xy^2m\) متشابه است. در صورتی که ضرایب یک جمله ای های متشابه را جمع کنیم، عبارت زیر به دست می‌آید:

\(\LARGE 3x^3mn+5xy^2m\)

در قسمت پایانی این مثال از درسنامۀ عبارت های جبری نهم باید چندجمله ای بالا را نسبت به توان‌های نزولی \(\Large y\) مرتب کنیم. همان‌طور که گفتیم، باید ببینیم در کدام یک جمله ای، متغیر \(\Large y\) بیشترین توان را دارد. آن را اول نوشته و سپس بقیۀ یک جمله ای ها را از توان بزرگ \(\Large y\) به توان کوچک \(\Large y\) بنویسیم. در یک جمله ای \(\Large 3x^3mn\) ، توان \(\Large y\) برابر با \(\Large 0\) است. در یک جمله ای \(\Large 5xy^2m\)، توان \(\Large y\) برابر با \(\Large 2\) است. بنابراین ابتدا \(\Large 5xy^2m\) را نوشته و سپس \(\Large 3x^3mn\) را می‌نویسیم:

\(\LARGE 5xy^2m+3x^3mn\)

برای آشنایی بیشتر با این مبحث حتما درسنامه تابع چند جمله ای به زبان ساده را مطالعه کنید

زنگ آخر کلاس عبارت های جبری نهم

در درسنامه‌ای که از ریاضی نهم که با هم خواندیم، ابتدا یک حمله ای ها را معرفی کردیم. سپس نحوۀ به دست آوردن درجۀ یک یک جمله ای نسبت به منغیرهای آن را بررسی کردیم. بر همین اساس، یک جمله ای های مشابه را معرفی کردیم. همان طور که دیدید، برای جمع و تفریق چند جمله ای ها باید ضرایب یک جمله ای ها را با یکدیگر جمع و یا از یکدیگر تفریق می‌کردیم.

ما در ریاضیکا آماده‌ی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با این مبحث دارید، در دیدگاه‌ها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند ‌داد.