آموزش ریاضی پایه نهم
اجتماع و اشتراک و تفاضل مجموعه ها ➖➕ – همراه با مثال و تصاویر!
قصد داریم به مبحث شیرین اجتماع و اشتراک و تفاضل مجموعه ها از ریاضی نهم بپردازیم. سعی کردیم طوری درسنامه را تنظیم کنیم تا با مطالعۀ آن، مبحث را به سادگی درک کنید. در پایان این درسنامه به راحتی میتوانید به سوالات زیر پاسخ دهید:
- اشتراک و اجتماع مجموعه ها به چه معنی است؟
- تعریف تفاضل دو مجموعه چیست؟
- تعداد عضوهای مجموعه را چگونه نمایش میدهند؟
اشتراک دو مجموعه
دو مجموعۀ \( \Large A \) و \( \Large B \) را در نظر بگیرید. به مجموعۀ اعضایی که هم عضوِ \( \Large A \) هستند و هم عضوِ \( \Large B \)، اشتراک دو مجموعۀ \( \Large A \) و \( \Large B \) میگویند. به زبان ساده تر، مجموعۀ عضوهای مشترک بین \( \Large A \) و \( \Large B \)، اشتراک \( \Large A \) و \( \Large B \) نام دارد. اشتراک \( \Large A \) و \( \Large B \) را با نماد \( \Large A\cap B \) نمایش میدهند. همچنین میتوانیم اشتراک دو مجموعه را با نمادهای ریاضی، به صورت زیر نمایش دهیم:
\( \Large A\cap B=\{x| x\in A\) و \( \Large x\in B\}\)
به سادگی میتوان دید که اشتراک هر دو مجموعه، زیرمجموعۀ هر کدام از آنهاست؛ زیرا هر عضوی که در اشتراک دو مجموعه وجود داشته باشد، در هر یک ازآنها نیز موجود است. بنابراین داریم:
\( \Large A\cap B\subseteq A\)
\( \Large A\cap B\subseteq B\)
خاصیت جابجایی اشتراک
با توجه به تعریف اشتراک دو مجموعه، اشتراک دو مجموعه دارای خاصیت جابجایی است. یعنی حاصل \( \Large A\cap B \) و \( \Large B\cap A \) برای هر دو مجموعۀ دلخواه برابر است.
به مثالهای زیر از مبحث اجتماع و اشتراک و تفاضل مجموعه ها از ریاضی نهم دقت کنید.
مثال از اشتراک دو مجموعه
مثال 1: اگر \( \Large A=\{1, 3, 8\} \) و \( \Large B=\{2, 3, 10, 8\} \) باشد، \( \Large A \cap B \) را به دست آورده و نمودار وِن آن را رسم کنید.
حل: دو عدد 3 و 8، هم در مجموعۀ \( \Large A \) وجود دارند و هم در مجموعۀ \( \Large B \). بنابراین \( \Large A\cap B \) برابر است با:
\( \LARGE A\cap B=\{3, 8\} \)
در شکل زیر، نمودار وِن \( \Large A \) و \( \Large B \) را رسم کردهایم. همانطور که میبینید، \( \Large A\cap B \) در شکل هاشور خورده است.
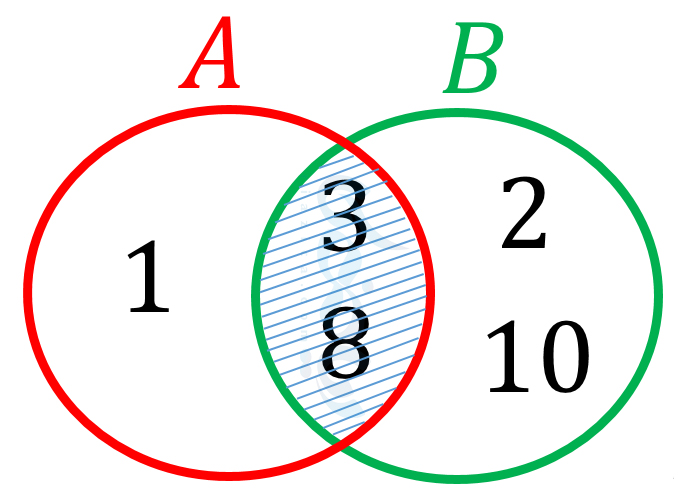
مثال 2: اگر مجموعۀ مضارب طبیعی عدد 2 را با \( \Large M \) و مجموعۀ مضارب طبیعی عدد 3 را با \( \Large N \) نمایش دهیم، \( \Large M\cap N \) را مشخص کنید.
حل: \( \Large M\cap N \) برابر است با مجموعۀ اعدادی که هم مضرب 2 هستند و هم مضرب 3. بنابراین \( \Large M\cap N\) برابر است با مجموعۀ مضارب طبیعی عدد 6. میتوانیم \( \Large M\cap N\) را با استفاده از نمادهای ریاضی به صورت زیر نمایش دهیم:
\( \Large M\cap N=\{6k|k \in \mathbb{N}\}\)
حالت خاص اشتراک دو مجموعه
اگر برای دو مجموعۀ \( \Large A \) و \( \Large B \) داشته باشیم \( \Large A\subseteq B\)، آنگاه اشتراک دو مجموعه چه خواهد شد؟ برای به دست آوردن اشتراک دو مجموعه به دنبال عضوهایی هستیم که هم در \( \Large A \) و هم در \( \Large B\) وجود داشته باشند. تمام اعضای \( \Large A \)، عضو \( \Large B\) نیز هستند. بنابراین داریم:
\( \LARGE A\cap B=A \)
در نمودار ون زیر نیز میتوانید اشتراک دو مجموعه در این حالت خاص را مشاهده کنید.
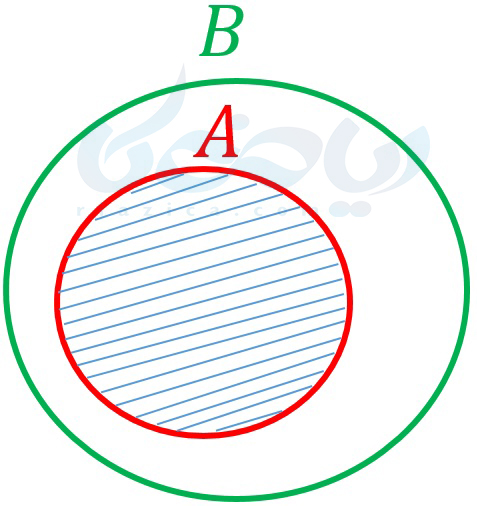
اجتماع دو مجموعه
دو مجموعۀ \( \Large A \) و \( \Large B \) را در نظر بگیرید. اجتماع \( \Large A \) و \( \Large B \) برابر است با مجموعۀ تمام اعضایی که حداقل عضو یکی از دو مجموعۀ \( \Large A \) و \( \Large B \) باشند. به زبان ساده تر، اگر اعضای \( \Large A \) و اعضای \( \Large B \) را در یک مجموعه کنار هم قرار دهیم (بدون تکرار عضو)، اجتماع \( \Large A \) و \( \Large B \) تشکیل میشود. اجتماع دو مجموعۀ \( \Large A \) و \( \Large B \) را با \( \Large A\cup B \) نمایش میدهیم. همچنین میتوانیم \( \Large A\cup B \) را با استفاده از نمادهای ریاضی، به صورت زیر نمایش دهیم:
\( \Large A\cup B=\{x| x\in A\) یا \( \Large x\in B\}\)
به سادگی میتوان دید که هر مجموعه، زیرمجموعۀ اجتماع آن مجموعه با مجموعۀ دیگر است؛ زیرا هر عضو یک مجموعه، در اجتماع آن مجموعه با مجموعۀ دیگر نیز وجود دارد. بنابراین داریم:
\( \Large A\subseteq A\cup B\)
\( \Large B\subseteq A\cup B\)
جابجایی بودن اجتماع در مبحث اجتماع و اشتراک و تفاضل مجموعه ها
با توجه به تعریف اجتماع دو مجموعه، اجتماع دو مجموعه نیز مانند اشتراک دارای خاصیت جابجایی است. یعنی حاصل \( \Large A\cup B \) و \( \Large B\cup A \) برای هر دو مجموعۀ دلخواه برابر است.
به مثالهای زیر از مبحث اجتماع و اشتراک و تفاضل مجموعه ها از ریاضی نهم دقت کنید.
مثالهایی از اجتماع دو مجموعه
مثال 3: اگر \( \Large A=\{1, 3, 8\} \) و \( \Large B=\{2, 3, 10, 8\} \) باشد، \( \Large A \cup B \) را به دست آورده و نمودار وِن آن را رسم کنید.
حل: عدد 1 در مجموعۀ \( \Large A \)، اعداد 2 و 10 در مجموعۀ \( \Large B \) و اعداد 3 و 8 هم در مجموعۀ \( \Large A \) و هم در مجموعۀ \( \Large B \) هستند. \( \Large A\cup B \) از کنار هم قرار دادن این اعداد به دست میآید. بنابراین، \( \Large A\cup B \) برابر است با:
\( \Large A\cup B=\{1, 2, 10, 3, 8\} \)
در شکل زیر، نمودار وِن \( \Large A \) و \( \Large B \) را رسم کردهایم. همانطور که میبینید، \( \Large A\cup B \) در شکل هاشور خورده است.
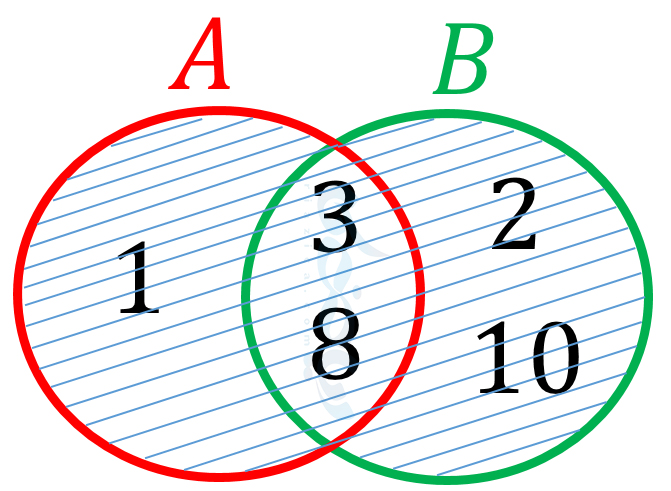
مثال 4: اگر مجموعۀ شمارندههای طبیعی عدد 14 را با \( \Large A \) و مجموعۀ شمارندهای طبیعی عدد 22 را با \( \Large B \) نمایش دهیم، \( \Large A\cup B \) را به دست آورید.
حل: مجموعۀ شمارندههای طبیعی عدد 14 برابر است با:
\( \LARGE A=\{1, 2, 7, 14\} \)
مجموعۀ شمارندههای طبیعی عدد 22 برابر است با:
\( \LARGE B=\{1, 2, 11, 22\} \)
طبق تعریف، \( \Large A\cup B \) برابر است با مجموعۀ تمام اعضایی که حداقل عضو یکی از دو مجموعه باشند. بنابراین، \( \Large A\cup B \) برابر است با:
\( \Large A\cup B=\{1, 2, 7, 14, 11, 22\} \)
حالت خاص اجتماع دو مجموعه
اگر برای دو مجموعۀ \( \Large A \) و \( \Large B \) داشته باشیم \( \Large A\subseteq B \)، آنگاه اجتماع دو مجموعه چه خواهد شد؟ گفتیم به زبان ساده، اجتماع دو مجموعه، از کنار هم قرار دادن اعضای دو مجموعه (بدون تکرار عضوها) به دست میآید. در این مثال خاص، تمام اعضای \( \Large A \) در \( \Large B \) نیز وجود دارند. پس، اگر اعضای \( \Large A \) و \( \Large B \) را کنار هم قرار دهیم و عضوهای تکراری را که همان عضوهای \( \Large A \) است حذف کنیم، تنها مجموعۀ \( \Large B \) باقی میماند. بنابراین داریم:
\( \LARGE A\cup B=B \)
در نمودار ون زیر نیز میتوانید اجتماع دو مجموعه را در این حالت مشاهده کنید.
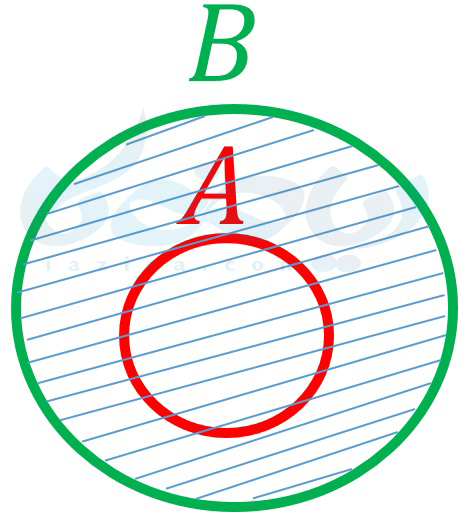
تفاضل دو مجموعه
مجموعۀ \( \Large A \) منهای \( \Large B \) برابر است با مجموعۀ تمام اعضایی که عضو \( \Large A \) هستند ولی عضو \( \Large B \) نیستند. به زبان ساده تر، اگر عضوهایی که بین \( \Large A \) و \( \Large B \) مشترک هستند را از مجموعۀ \( \Large A \) حذف کنیم، مجموعۀ \( \Large A \) منهای \( \Large B \) به دست میآید. مجموعۀ \( \Large A \) منهای \( \Large B \) را با \( \Large A-B \) نمایش میدهیم. همچنین میتوانیم \( \Large A-B \) را با استفاده از نمادهای ریاضی به صورت زیر نمایش دهیم:
\( \Large A- B=\{x| x\in A\) و \( \Large x\not\in B\}\)
غیر جابجایی بودن تفاضل در مبحث اجتماع و اشتراک و تفاضل مجموعه ها
تفاضل دو مجموعه بر خلاف اشتراک و اجتماع، دارای خاصیت جابجایی نیست. یعنی لزوماً حاصل \( \Large A-B \) با \( \Large B-A \) برابر نیست. از تعریف تفاضل میتوان به این نکته پی ببرد. برای درک بهتر این موضوع، به مثالهای بعد از مبحث اجتماع و اشتراک و تفاضل مجموعه ها از ریاضی نهم دقت کنید.
مثالهایی از تفاضل دو مجموعه
مثال 5: اگر \( \Large A=\{1, 3, 8\} \) و \( \Large B=\{2, 3, 10, 8\} \) باشد، \( \Large A – B \) و \( \Large B – A \) را به دست آورده و نمودار وِن آن را رسم کنید.
حل: اعداد 3 و 8، هم عضو مجموعۀ \( \Large A \) هستند، هم عضو مجموعۀ \( \Large B \). پس، اگر 3 و 8 را از مجموعۀ \( \Large A \) حذف کنیم، \( \Large A-B \) به دست میآید. بنابراین، \( \Large A-B \) برابر است با مجموعۀ \( \LARGE\{1\}\).
نمودار وِن \( \Large A \) و \( \Large B \) نیز در شکل زیر رسم شده است. همانطور که میبینید، \( \Large A – B \) در شکل هاشور خورده است.
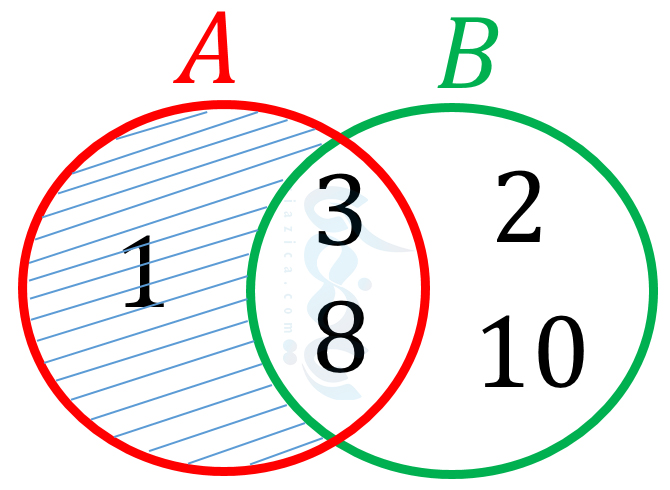
از طرفی اگر اعداد 3 و 8 را از مجموعۀ \( \Large B \) حذف کنیم، مجموعۀ \( \Large B-A \) به دست میآید. یعنی مجموعۀ \( \Large B-A \) برابر است با \( \Large \{2, 10\} \). نمودار ون مجموعۀ \( \Large B-A \) نیز به شکل زیر است:
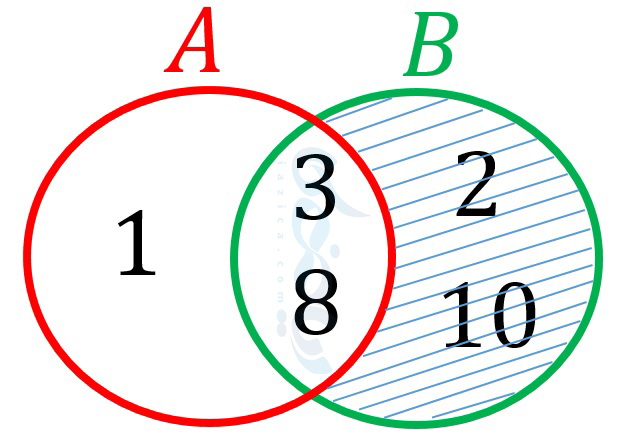
همان طور که در این مثال دیدید، حاصل \( \Large B-A \) با \( \Large B-A \) برابر نشد.
مثال 6: مجموعۀ \( \Large \mathbb{N}-W \) و \( \Large W-\mathbb{N} \) را به دست آورید.
حل: مجموعۀ اعداد طبیعی و حسابی به ترتیب برابرند با:
\( \LARGE\mathbb{N}=\{1, 2, 3, \dots\} \)
\( \LARGE W=\{0, 1, 2, 3, \dots\} \)
تمام اعدادی که عضو \( \Large \mathbb{N} \) هستند، عضو \( \Large W\) هم هستند. یعنی اگر اعضای مشترک \( \Large \mathbb{N} \) و \( \Large W\) را از \( \Large \mathbb{N} \) حذف کنیم، عضوی از \( \Large \mathbb{N} \) باقی نمیماند. بنابراین داریم:
\( \LARGE \mathbb{N}-W=\emptyset \)
اما عدد 0 بین \( \Large \mathbb{N}\) و \( \Large W \) مشترک نیست. بنابراین اگر اعضای مشترک \( \Large \mathbb{N}\) و \( \Large W\) را از \( \Large W\) حذف کنیم، عدد 0 باقی ماند. بنابراین داریم:
\( \LARGE W-\mathbb{N}=\{0\} \)
حالتهای خاص تفاضل دو مجموعه در مبحث اجتماع و اشتراک و تفاضل مجموعه ها
اگر اشتراک دو مجموعۀ \( \Large A \) و \( \Large B\) تهی باشد، اصطلاحاً میگوییم \( \Large A \) و \( \Large B \) جدا از هم هستند. در این حالت، چون \( \Large A \) و \( \Large B \) هیچ عضو مشترکی ندارند، داریم:
\( \LARGE A-B=A \)
\( \LARGE B-A=B\)
یک حالت خاص دیگر برای تفاضل دو مجموعه وجود دارد. اگر \( \Large A\subseteq B \) باشد، تمام اعضای \( \Large A \) در \( \Large B \) نیز هستند. بنابراین اگر اعضای مشترک \( \Large A \) و \( \Large B\) را از \( \Large A \) حذف کنیم، عضوی باقی نخواهد ماند. بنابراین داریم:
\( \LARGE A-B=\emptyset\)
در مثال 6 نیز میتوانید این موضوع را مشاهده کنید.
نکته :با توجه به مطلب بالا اگر دو مجموعه برابر باشند\( \LARGE A=B\) آنگاه تفاضل آنها باهم برابر وتهی میشود.
\( \LARGE A-B= B-A=\emptyset\)
تعداد عضوهای یک مجموعه در مبحث اجتماع و اشتراک و تفاضل مجموعه ها
تعداد عضوهای یک مجموعۀ دلخواه مانند \( \Large A \) را با \( \Large n(A)\) نشان میدهیم (لازم به ذکر است که این تعریف برای مجموعههای متناهی است. دوستانی که علاقهمند هستند، میتوانند در مورد مفهوم کاردینال که مشابه با تعداد اعضای یک مجموعه است و برای مجموعههای نامتناهی نیز قابل تعمیم است، مطالعه کنند).
به مثالهای زیر از مبحث اجتماع و اشتراک و تفاضل مجموعه ها از ریاضی نهم دقت کنید.
مثال از تعداد عضوهای یک مجموعه
مثال 7: اگر \( \Large A=\{2, 5, 9, f\}\) و \( \Large B=\{5, 1, e, f\}\) باشد، \( \Large n(A\cap B) \) و \( \Large n(A\cup B) \) را به دست آورید.
حل: اشتراک و اجتماع دو مجموعۀ \( \Large A\) و \( \Large B\) به ترتیب برابر است با:
\( \LARGE A\cap B=\{5, f\}\)
\( \LARGE A\cup B=\{1, 2, 5, 9, e, f\}\)
تعداد اعضای مجموعۀ \( \Large A\cap B\) برابر با 2 و تعداد اعضای مجموعۀ \( \Large A\cup B\) برابر با 6 است. بنابراین داریم:
\( \LARGE n(A\cap B)=2\)
\( \LARGE n(A\cup B)=6\)
ویدیو از اجتماع واشتراک و تفاضل مجموعه ها
در این ویدیو ما با چند مثال مفهوم اجتماع واشتراک وتفاضل مجموعه ها را توضیح داده ایم.
زنگ آخر کلاس اجتماع و اشتراک و تفاضل مجموعه ها
در دسنامهای که خواندیم، اشتراک، اجتماع و تفاضل دو مجموعه را به همراه رسم نمودار وِن و حل مثال بررسی کردیم. همچنین، نحوۀ نمایش تعداد اعضای یک مجموعه را نشان داده و مثالی از آن حل کردیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث اجتماع و اشتراک و تفاضل مجموعه ها دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.




عالی بود خدا قوتتون بده
سلام و عرض ادب
ممنون از توجهی که داشتید.
موفق باشید.
ببخشید ‘(A’-B) -C هاشور رو نمودار ون چیه
سلام ببخشید امکان داره در شرایط خاصی دو مجموعه A-B=B-A باشد؟؟
با سلام وعرض ادب
فقط در حالتی که دو مجموعه مساوی باشند تفاضل آنها برابر است
خیر اشتباه است
سلام دوست عزیز
در حالت کلی غلطه مگه اینکه دو مجموعه برابر باشن
اشتراکها: جواد
با سلام ووقت به خیر
خوشحالیم که براتون مفید واقع شده
پیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
خیلی جامع و کامل بود واقعا عالی بود عالی
سپاس از شما دوست عزیز.
سلام خسته نباشید ببخشید من فرق بین اشتراک و اجتماع رو نمیفهمم?
با سلام واحترم
عزیزم اینقد زیبا گفتیم اشتراک دو مجموعه یعنی عضوهای مشترک واجتمع یعنی همه عضوهای دو مجموعه روی هم
سلام لطفاً میشه تناسب معکوس رو بهم توضیح بدین لطفاً خیلی فوری نیاز دارم?
با سلام
به پست تناسب در دسته بندی آموزشهای پایه یازدهم مراجعه کنید
اشتراک یعنی هم عضو b باشه هم عضو a ولی اجتماعی یعنی همه عضو ها حتی اگر عضو a باشد ولی عضو b نباشد اشکالی ندارد
با سلام
ممنون از پاسخگویی شما در مورد اجتماع بهتر بگیم شامل عضوها هر دو مجموعه هست چه مشترک چه غیر مشترک
سلام خسته نباشید اشتراک هم خانواده مشترک هست یعنی عضوهای مشترک اجتماع هم یعنی همه عضوها یه جا جمع بشن با تشکر فراوان
با سلام ممنون از پاسخگویی شما
عالی بود دستتون درد نکنه ولی اجتماع و اشتراک یک مجموعه ای که اسمش مثلا سی باشه با تهی چی میشه ؟؟ و این که تفاضل دو مجموعه اجتماعش با تفاضل دو مجموعه دیگه چطور میشه ؟؟؟
با سلام واحترام
اشتراک هر مجموعه با تهی میشود تهی واجتماع هر مجموعه با تهی میشود خود مجموعه جواب سوال دوم شما بستگی به مجموعه ها داره
سلام خسته نباشید
ببخشید AاشتراکB و
BاجتماعA
چجوری باید جوابو بدست اورد
با سلام واحترام پست رو خوب بخونید پاسخ میگیرید
یه چیزی داشتیم بین مجموعه ها مثلا A ^ B (علامته توان نیست شبیه مثلثه یه جورایی دلتا رو کیبورد پیداش نکردم)، این چی میشه لطف کنید یه توضیحی در موردش بدبد.
سلام وعرض ادب
میگن دو مجموعه متقارن یعنی اجتماع دو مجموعه بدون عضوهای مشترک یا به عبارت اجتماع تفاضلهاشون
سلام
یه سوال داشتم.
اشتراک دو مجموعهAوB را داریم آنگاهA_Bچی میشه؟
با سلام وعرض ادب
حتما باید مجموعه A رو هم داشته باشیم از داخلش عضوهای مشترک رو برداریم میشهA-B
سلام .لطفا تفاضل متقارن رو هم تو سایت آپلود کنید ممنون
با سلام وعرض ادب
چشم به زودی
سلام . توضیحات عالی بودن .فقط تفاضل متقارن رو هم تو سایت آپلود کنید.لطفا
با سلام .
تفاضل یک مجموعه با تهی چی میشه ؟
با سلام
میشه خود مجموعه
عالی بود متشکرم
با سلام واحترام
ممنون دوست عزیز
سلام جواب A-تهی چیست
با سلام وعرض ادب
تهی میشه
ببخشید حالا اگه داشته باشم A∆B چی میشه
با سلام وادب
به این میگن تقارن دو مجموعه و اجتماع تفاضل این دو از هم میشه
سلام ببخشید اگه تو سوال بیادc منهای (AUB) باید چطور حلش کنیم؟(روی شکل)
با سلام قسمتهایی از سی رو باید هاشور بزنید که نه مال Aباشه نه مال B
سلام ببخشید اگر
(AUB ) = (AUC ) باشد انگاه B=C میشود؟ چرا؟
با سلام وادب
درسته چون اعضای Aکه مشترکند پس دومجموعه B,C برابر هستند یعنی اعضای آنها یکی هست که اجتماعشون یکی شده
عالی بود دستتون در نکنه کامل متوجه شدم ولی کاشکی درمورد متمم هم مینوشتین
با سلام وادب
خدا روشکر که مفید بوده در پستهای مربوط به پایه دهم متمم رو گفتیم
اشتراک هر مجموعه ای با خودش چه میشود؟
با سلام
میشه خودش
ali bod khoda ghovat
man farda emtehan daram o koli esteres
با سلام واحترام
با توکل به خدا وآرامش امتحان بدید حتما موفق میشید
سلام وقت بخیر
آیا دومجموعه ای داریم که تفاضل A-BوB-A هردو تهی باشه؟بامثال میشه توضیح بدید.ممنون
با سلام وادب
اگر دو مجموعه با هم برابر باشن
سلام ‘(a-b) چی میشه؟ هر جا میگردم قانونشو پیدا نمیکنم
سلام خسته نباشید ببخشيد جواب B زیر مجموعه ی) AاجتماعB چی میشه
با سلام دوست عزیز این یه نکته هست در مورد اجتماع دو مجموعه که هر کدوم ار مجموعه ها زیر مجموعه اجتماع هستن
عالی کامل وکاربردی فقط کاش مثالهای بیشتری داشت
با سلام وادب
ممنون از نظر شما حتما در آینده مثالهای بیشتری قرار خواهیم داد
سلام دوستان!
بنظرم در تعریف مجموعه اجتماع باید داشته باشیم x€A یا x€B بعبارتی فقط مجموعه هایی که در A یا درB قرار دارند مورد بررسی قرار دهیم و از اضافه کردن اشتراک دو مجموعه خودداری کنیم
مثال{A={1 2 3 4 و {B={5 6 3 4
باشد
اجتماعAو{B={1 2 5 6
بنظرم ۳ و۴ حذف میشن و جزو اشتراک ها قرار میگیرند!
دوستان درست هستش؟؟؟؟
باسلام دوست عزیز
خیر دوست گرامی ذر منطق ریاضی وقتی بین دو گزاره یا می آید یعنی یا عضو A یا عضو B یا عضو هر دو بنابراین باید در اجتماع عضو های مشترک را هم بنویسیم
خیر غلط هست
ممنون از پاسخگویی شما
با سلام خیر عضوهای مشترک هم نوشته میشه
دمتون گرم خیلی ساده یاد داده بودین ممنون
یا سلام وادب
دم شما هم گرم از کامنت زیباتون
خیلی طولانی ولی خوبه
با سلام ممنون از نظر شما برای اینکه مطلب رو کامل بگیم مجبوریم طولانی بگیم
با سلام اگر A اجتماع B مساوی A باشد جواب B منهای A احتمالا تهی میشود اگر آن را بخواهیم با نمودار ون نشان بدین چجوری خواهد بود
باسلام
این یعنی Bزیر مجموعه Aاست پس این دو را داخل هم بکشید که A دایره بزرگتر است
بسی خیلی خوب بود🤓
با سلام ممنون از لطف شما