بردار انتقال ریاضی هفتم ➡️✔️ – مرحله به مرحله!

در درسنامهٔ بردار انتقال ریاضی هفتم قصد داریم چگونگی انتقال یک شکل به وسیلهٔ یک بردار را بررسی خواهیم کنیم. بدین منظور، ابتدا چگونگی انتقال یک نقطه به وسیلهٔ یک بردار را بررسی کرده و سپس با انتقال تمام نقاط یک شکل، آن را انتقال می‌دهیم. سعی می‌کنیم با حل مثال، به درک بهتر شما از این مبحث کمک کنیم. با ما تا انتهای درسنامه همراه باشید.

انتقال نقطه به وسیلهٔ بردار

در درسنامهٔ تبدیلات هندسی ریاضی هفتم با تبدیل انتقال آشنا شدید. می‌توان یک نقطه را با استفاده از یک بردار انتقال داد. برای این کار کافی است طول نقطه را با طول بردار و عرض آن را با عرض بردار جمع کنیم تا مختصات نقطهٔ انتقال یافته به دست بیاید. مثلاً در شکل زیر، نقطهٔ \(\Large A=\begin{bmatrix} 1\\ 2 \end{bmatrix}\) را با بردار \(\Large \overrightarrow{AB}=\begin{bmatrix} 3\\ 2 \end{bmatrix}\) انتقال می‌دهیم تا نقطهٔ \(\Large B=\begin{bmatrix} 4\\ 4 \end{bmatrix}\) حاصل شود:

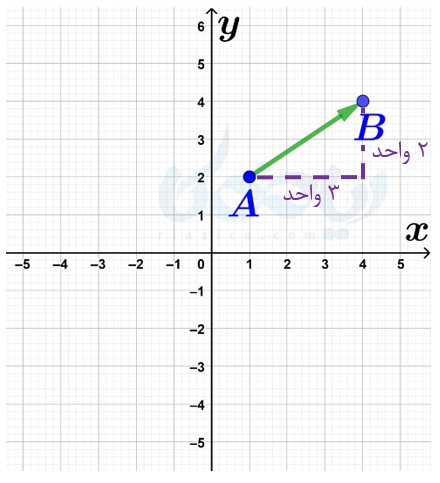
همان طور که در شکل بالا می بینید، مختصات نقطهٔ \(\Large B\) از جمع مختصات نقطهٔ \(\Large A\) با مختصات بردار \(\Large \overrightarrow{AB}\) به دست می‌آید. یعنی می‌توانیم بنویسیم:

\(\LARGE \begin{bmatrix} 1\\ 2 \end{bmatrix}+\begin{bmatrix} 3\\ 2 \end{bmatrix}=\begin{bmatrix} 4\\ 4 \end{bmatrix}\)

همین کار را می‌توانیم برای هر بردار دلخواهی انجام دهیم؛ یعنی می‌توانیم برای هر برداری، جمع متناظر با آن بردار را بنویسیم. چرا که می‌توان به هر بردار به عنوان یک بردار انتقال نگاه کرد که نقطهٔ ابتدای آن را به نقطهٔ انتهای آن می‌برد. برای اینکه بهتر متوجه شوید، به مثال بعدی از درسنامهٔ بردار انتقال ریاضی هفتم توجه کنید.

مثال

مثال 1 از بردار انتقال ریاضی هفتم: جمع متناظر با بردار \(\Large \overrightarrow{CD}\) که در شکل زیر مشخص شده را بنویسید.

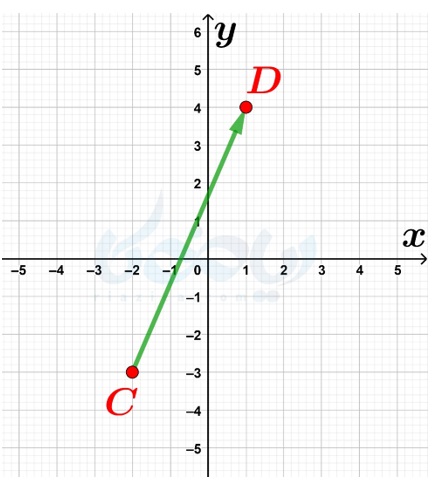
حل: می‌توانیم تعداد واحدهایی که درجهت محور طول‌ها و عرض‌ها از نقطهٔ \(\Large C\) تا نقطهٔ \(\Large C\) پیموده‌ایم را به صورت زیر نشان دهیم:

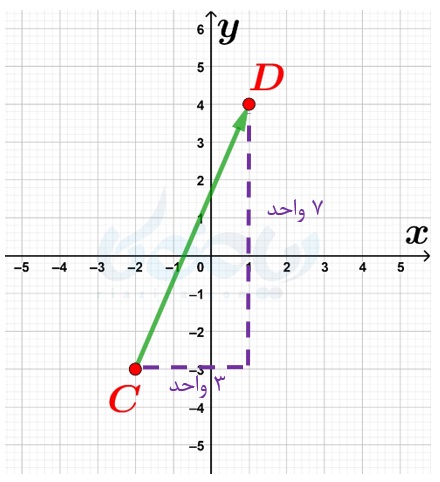
مختصات نقاط \(\Large C\) و \(\Large D\) و بردار \(\Large \overrightarrow{CD}\) به صورت زیر است:

\(\LARGE C=\begin{bmatrix} -2\\ -3 \end{bmatrix} \)

\(\LARGE D=\begin{bmatrix} 1\\ 4 \end{bmatrix} \)

\(\LARGE \overrightarrow{CD}=\begin{bmatrix} 3\\ 7 \end{bmatrix} \)

اگر مختصات نقطهٔ \(\Large C\) را با مختصات بردار \(\Large \overrightarrow{CD}\) جمع کنیم، مختصات نقطهٔ \(\Large D\) به دست می‌آید. بنابراین جمع متناظر با بردار \(\Large \overrightarrow{CD}\) به صورت زیر است:

\(\LARGE \begin{bmatrix} -2\\ -3 \end{bmatrix}+\begin{bmatrix} 3\\ 7 \end{bmatrix}=\begin{bmatrix} 1\\ 4 \end{bmatrix} \)

به قسمت بعدی از درسنامهٔ بردار انتقال ریاضی هفتم توجه کنید.

بررسی یک حالت خاص

گاهی می‌خواهیم نقطه‌ای را به وسیلهٔ برداری که ابتدای آن بر نقطهٔ مورد نظر منطبق نیست انتقال دهیم. در این صورت کافی است برداری برابر با بردار داده شده که نقطهٔ ابتدای آن بر نقطهٔ مورد نظر منطبق است، رسم کرده و سپس انتقال را انجام دهیم. به طور مثال فرض کنید می‌خواهیم نقطهٔ \(\Large A\) در شکل زیر را به وسیلهٔ بردار \(\Large \overrightarrow{t}\) انتقال دهیم.

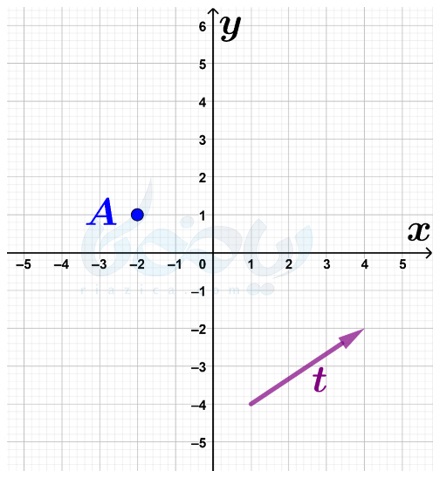
برای این کار، ابتدا یک بردار برابر با بردار \(\Large \overrightarrow{t}\) که ابتدای آن بر نقطهٔ \(\Large A\) منطبق است رسم می‌کنیم. همان طور که در درسنامهٔ بردارهای مساوی و قرینه ریاضی هفتم خواندید، برداری که هم‌اندازه، هم‌راستا و هم‌جهت با بردار \(\Large \overrightarrow{t}\) باشد، با آن برابر است. بنابراین، برداری هم‌اندازه‌، هم‌راستا و هم‌جهت با بردار \(\Large \overrightarrow{t}\) که نقطهٔ ابتدایی آن بر نقطهٔ \(\Large A\) منطبق است رسم کرده و به آن بردار \(\Large \overrightarrow{t’}\) می‌گوییم:

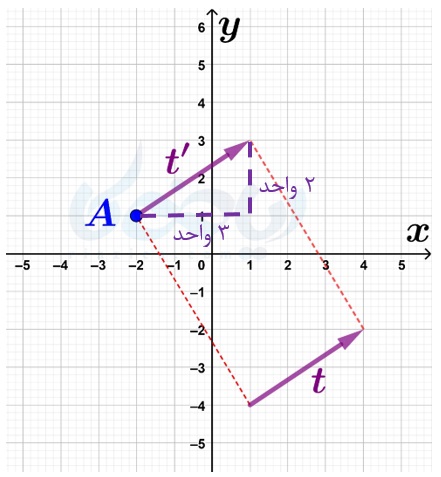
مختصات بردار \(\Large \overrightarrow{t’}\) برابر با \(\Large \begin{bmatrix} 3\\ 2 \end{bmatrix}\) است. پس، اگر از نقطهٔ \(\Large A\) سه واحد در جهت محور طول‌ها و دو واحد در جهت محور عرض‌ها حرکت کنیم، نقطهٔ انتقال یافته که همان نقطهٔ \(\Large B\) است، به دست می‌آید:

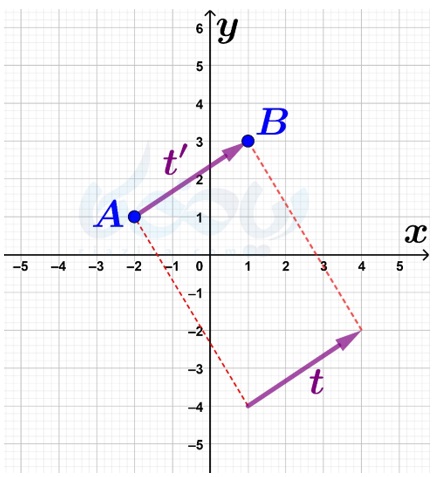
جمع متناظر با این انتقال که در واقع همان حاصل جمع مختصات نقطهٔ \(\Large A\) با مختصات بردار \(\Large \overrightarrow{t’}\) است نیز، به صورت زیر در می‌آید:

\(\LARGE \begin{bmatrix} -2\\ 1 \end{bmatrix}+\begin{bmatrix} 3\\ 2 \end{bmatrix}=\begin{bmatrix} 1\\ 3 \end{bmatrix} \)

به قسمت بعدی از درسنامهٔ بردار انتقال ریاضی هفتم توجه کنید.

انتقال شکل به وسیلهٔ بردار

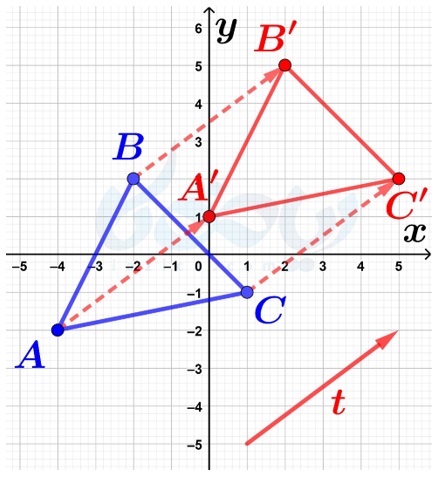
حال که انتقال نقطه به وسیلهٔ بردار را فرا گرفتیم، می‌توانیم اشکال را نیز به وسیلهٔ بردارها انتقال دهیم. کافی است تمام نقاط شکل را به همان روشی که برای انتقال نقطه گفتیم، انتقال دهیم. کار ما برای انتقال چند ضلعی‌ها راحت‌تر است؛ زیرا لازم نیست تمام نقاط چندضلعی را انتقال دهیم. از آنجاییکه انتقال، تبدیلی است که فاصلهٔ بین نقاط را حفظ می‌کند، کافی است رئوس یک چند ضلعی را انتقال داده و انتقال یافتهٔ آن‌ها را با حفط فواصل به هم وصل کنیم. مثلاً فرض کنید می‌خواهیم مثلث \(\Large ABC\) در شکل زیر را به وسیلهٔ بردار \(\Large \overrightarrow{t}\) انتقال دهیم:

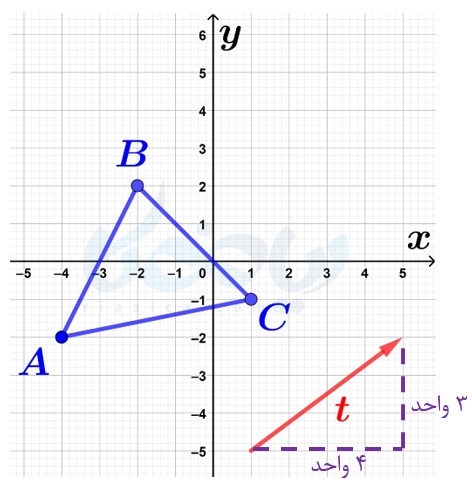
مختصات بردار \(\Large \overrightarrow{t}\) برابر با \(\Large \begin{bmatrix} 4\\ 3 \end{bmatrix}\) است. پس، اگر از هر یک از رئوس مثلث، چهار واحد در جهت محور طول‌ها و سه واحد در جهت محور عرض‌ها حرکت کنیم، نقاط انتقال یافته به دست می‌آیند:

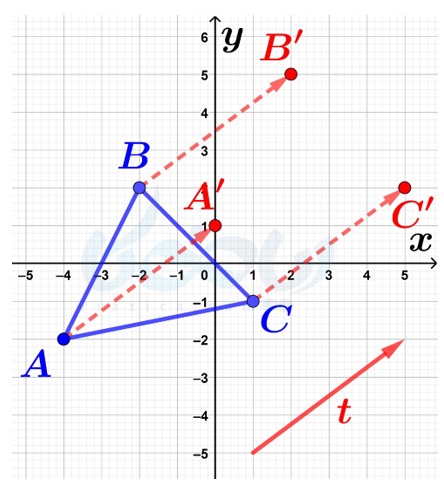
حال، نقاط انتقال یافته را که همان نقاط \(\Large A’\) و \(\Large B’\) و \(\Large C’\) هستند به هم وصل می‌کنیم:

برای علاقه‌مندان: ایزومتری‌ها تبدیلاتی هستند که فاصله را حفظ می‌کنند. در صورتی که علاقه‌مندید می‌توانید در مورد آن‌ها مطالعه کنید.

مثال از درسنامهٔ بردار انتقال ریاضی هفتم

مثال 2 از بردار انتقال ریاضی هفتم: چهارضلعی \(\Large ABCD\) را به وسیلهٔ بردار \(\Large \overrightarrow{t}\) انتقال دهید.

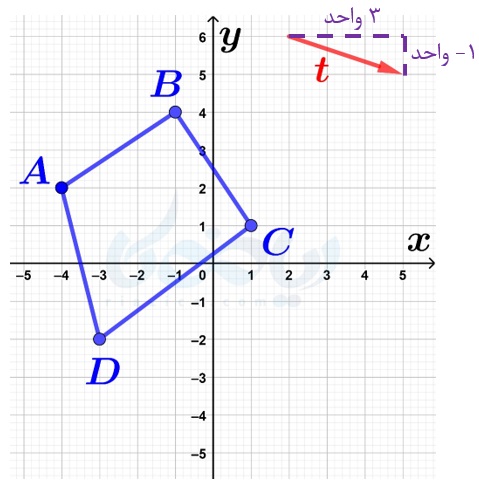
حل: هر کدام از نقاط \(\Large A\) و \(\Large B\) و \(\Large C\) و \(\Large D\) را به وسیلهٔ بردار \(\Large \overrightarrow{t}\) انتقال می‌دهیم تا به ترتیب، نقاط \(\Large A’\) و \(\Large B’\) و \(\Large C’\) و \(\Large D’\) حاصل شوند:

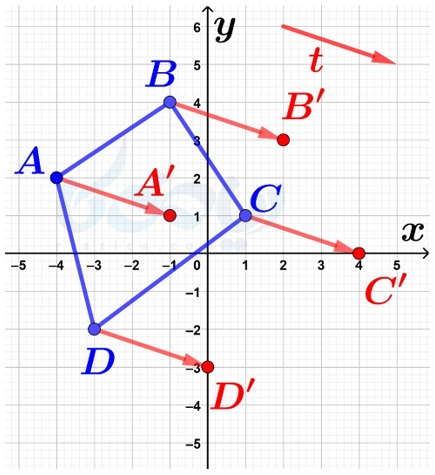
حال نقاط \(\Large A’\) و \(\Large B’\) و \(\Large C’\) و \(\Large D’\) را به هم وصل می‌کنیم تا شکل انتقال یافته حاصل شود:

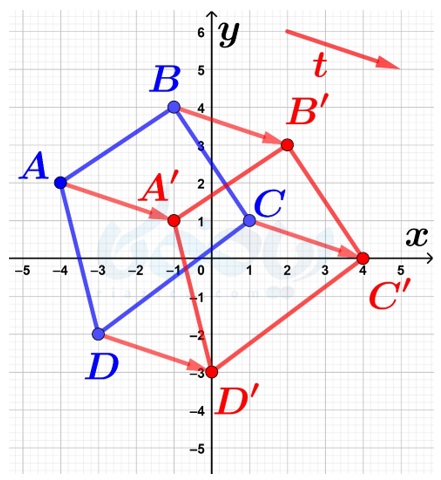
مثال از درسنامهٔ بردار انتقال ریاضی هفتم

مثال 3 از بردار انتقال ریاضی هفتم: نقطهٔ \(\Large A=\begin{bmatrix} m\\ n \end{bmatrix}\) را با بردار \(\Large \overrightarrow{t}=\begin{bmatrix} h\\ v \end{bmatrix}\) انتقال می‌دهیم. مختصات نقطهٔ حاصل را بیابید.

حل: کافی است مختصات نقطهٔ \(\Large A\) را با مختصات بردار \(\Large \overrightarrow{t}\) جمع کنیم:

\(\LARGE \begin{bmatrix} m\\ n \end{bmatrix}+\begin{bmatrix} h\\ v \end{bmatrix}=\begin{bmatrix} m+h\\ n+v \end{bmatrix} \)

بنابراین مختصات نقطهٔ انتقال یافته برابر با \(\Large \begin{bmatrix} m+h\\ n+v \end{bmatrix}\) است.

مثال

مثال 4 از بردار انتقال ریاضی هفتم: در شکل زیر، نقطهٔ \(\Large A\) را با بردار \(\Large \overrightarrow{t}\) انتقال داده‌ایم تا به نقطهٔ \(\Large A’\) برسیم. نقطهٔ \(\Large A’\) را به چه برداری انتقال دهیم تا دوباره به نقطهٔ \(\Large A\) برگردیم؟

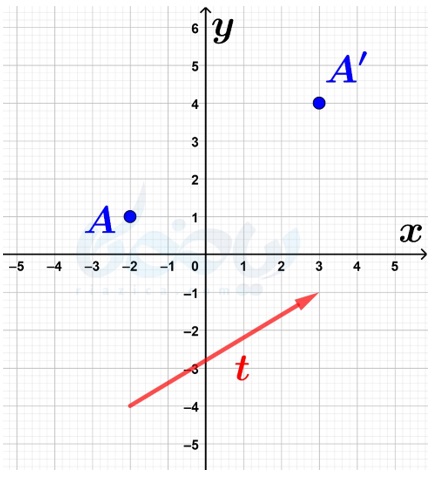
حل: کافی است برداری هم‌اندازه، هم‌راستا و در خلاف جهت بردار \(\Large \overrightarrow{t}\) رسم کرده تا از نقطهٔ \(\Large A’\) به نقطهٔ \(\Large A\) برگردیم:

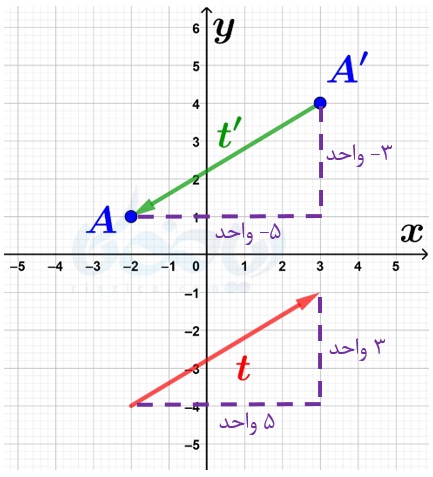
همان طور که در درسنامهٔ پاره خط جهت دار ریاضی هفتم گفتیم، برداری که هم‌اندازه، هم‌راستا و در خلاف جهت بردار دیگری باشد، قرینهٔ آن است. بنابراین در شکل بالا، بردار \(\Large \overrightarrow{t’}\)، قرینهٔ بردار \(\Large \overrightarrow{t}\) است. اگر مختصات بردارهای \(\Large \overrightarrow{t}\) و \(\Large \overrightarrow{t’}\) را بنویسیم، متوجه یک نکته خواهیم شد. مختصات بردارهای \(\Large \overrightarrow{t}\) و \(\Large \overrightarrow{t’}\) به صورت زیر است:

\(\LARGE \overrightarrow{t}=\begin{bmatrix} 5\\ 3 \end{bmatrix}\)

\(\LARGE \overrightarrow{t’}=\begin{bmatrix} -5\\ -3 \end{bmatrix}\)

همان طور که می‌بینید، مختصات بردارهای \(\Large \overrightarrow{t}\) و \(\Large \overrightarrow{t’}\) قرینهٔ یکدیگرند.

برای درک بهتر این مطلب  پستهای  پاره خط جهت دار و بردارهای مساوی وقرینه  و مختصات ریاضی هفتم مطالعه کنید و حواست باشه ما تمام درسهای ریاضی پایه هفتم رو به طور کامل برات تدریس کردیم حتما اونها رو هم مطالعه کن

زنگ آخر کلاس بردار انتقال ریاضی هفتم

در درسنامه‌ای که از ریاضی هفتم خواندیم، ابتدا انتقال نقطه با بردار را بررسی کردیم. سپس به انتقال شکل با بردار پرداختیم. همان طور که گفتیم برای انتقال چندضلعی‌ها با بردار کافی است رئوس آن را انتقال داده و سپس با حفظ فاصله، نقاط انتقال یافته را به هم وصل کنیم.

ما در ریاضیکا آماده‌ی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با بردار انتقال ریاضی هفتم دارید، در دیدگاه‌ها بنویسید. کارشناسان ما به سوال شما پاسخ  خواهند ‌داد.