آموزش ریاضی پایه هفتم
مختصات ریاضی هفتم 📈🔖 – محور و نواحی مختصاتی!
در درسنامهٔ مختصات ریاضی هفتم ابتدا نمایش نقاط صفحه با استفاده از محورهای مختصات را مرور میکنیم. سپس صفحه را با استفاده از محورها ناحیه بندی کرده و به هر یک شمارهای اختصاص میدهیم. در انتها نیز، همان طور که نقاط صفحه را با استفاده از مختصاتشان نشان دادیم، بردارها را نمایش خواهیم داد. سعی میکنیم با حل مثال، به درک بهتر شما از این مبحث کمک کنیم.
یادآوری محورهای مختصات
همانطور که میدانید، هر نقطه از صفحه را میتوان با استفاده از مختصات آن نمایش داد. مثلاً شکل زیر را در نظر بگیرید:
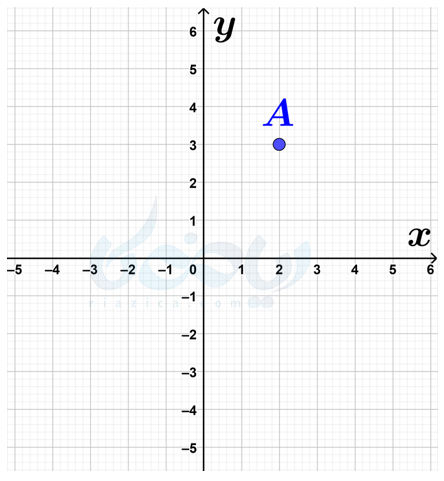
نقطهٔ \(\Large A\) در شکل بالا را میتوان با استفاده از مختصات آن به صورت \(\Large A=\begin{bmatrix} 2 \\ 3 \end{bmatrix}\) نمایش داد. درایهٔ بالایی(عدد بالایی)، نشان دهندهٔ طول و درایهٔ پایینی(عدد پایینی)، نشان دهندهٔ عرض نقطهٔ \(\Large A\) است.
برای علاقهمندان: دستگاه مختصاتی که در دورهٔ دبیرستان با آن کار میکنیم، دستگاه مختصات دکارتی است. اما میتوان نقاط صفحه را با استفاده از دستگاه مختصات استوانهای، کروی و یا دیگر دستگاهها نیز نمایش داد. در صورتی که علاقهمندید میتوانید در این مورد مطالعه کنید.
مثال از مختصات ریاضی هفتم
مثال 1: مختصات نقاط \(\Large A\) و \(\Large B\) و \(\Large C\) که در شکل زیر مشخص شدهاند را بنویسید.
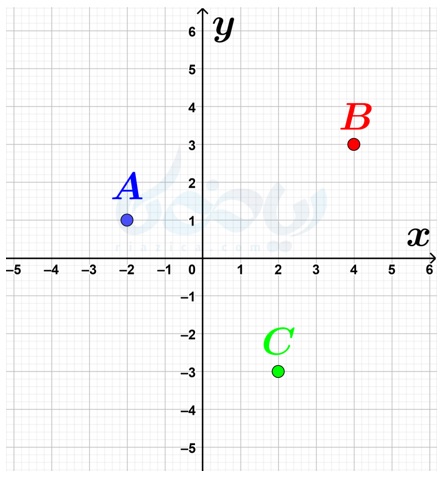
حل: طول نقطهٔ \(\Large A\) برابر با \(\Large -2\) و عرض آن برابر با \(\Large 1\) است؛ بنابراین مختصات نقطهٔ \(\Large A\) برابر است با \(\Large \begin{bmatrix} -2 \\ 1 \end{bmatrix}\). طول نقطهٔ \(\Large B\) برابر با \(\Large 4\) و عرض آن برابر با \(\Large 3\) است؛ بنابراین مختصات نقطهٔ \(\Large B\) برابر است با \(\Large \begin{bmatrix} 4 \\3 \end{bmatrix}\). طول نقطهٔ \(\Large C\) برابر با \(\Large 2\) و عرض آن برابر با \(\Large -3\) است؛ بنابراین مختصات نقطهٔ \(\Large C\) برابر است با \(\Large \begin{bmatrix} 2 \\ -3 \end{bmatrix}\).
ناحیههای صفحه
میتوان صفحه را با استفاده از محورهای مختصات به چهار ناحیه تقسیم کرد. در شکل زیر این چهار ناحیه را شمارهگذاری کردهایم:
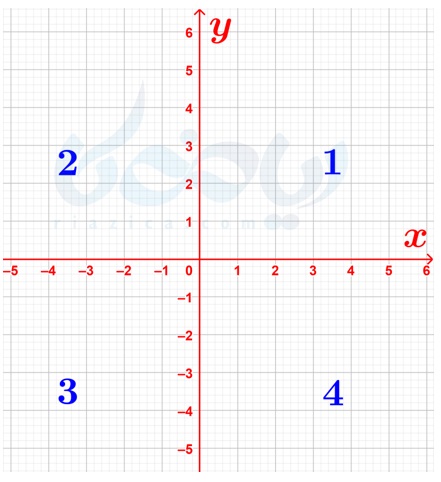
نکته:برای به خاطر سپردن یادتون باشه نامگداری خلاف گردش عقربه های ساعت می باشد.
به عبارت دیگر، هر یک از نقاط صفحه (به غیر از مبدأ) با توجه به طول و عرضی که دارند، به صورت زیر در یکی از این نواحی قرار میگیرد:
- ناحیهٔ 1: نقاطی که دارای \(\Large x>0\) و \(\Large y>0\) هستند.(طول وعرض مثبت)
- ناحیهٔ 2: نقاطی که دارای \(\Large x<0\) و \(\Large y>0\) هستند.(طول منفی وعرض مثبت)
- ناحیهٔ 3: نقاطی که دارای \(\Large x<0\) و \(\Large y<0\) هستند.(طول وعرض منفی)
- ناحیهٔ 4: نقاطی که دارای \(\Large x>0\) و \(\Large y<0\) هستند.( طول مثبت وعرض منغی)
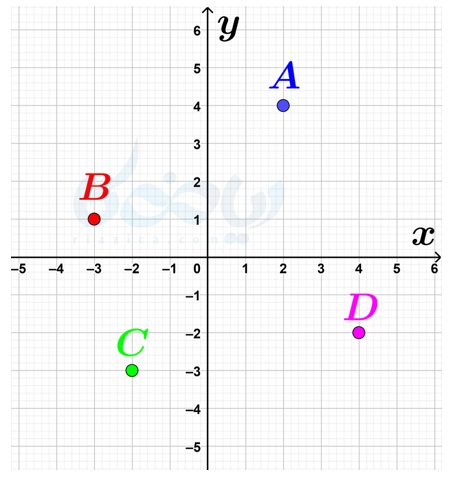
مثلاً در شکل زیر، نقطهٔ \(\Large A\) در ناحیهٔ 1، نقطهٔ \(\Large B\) در ناحیهٔ 2، نقطهٔ \(\Large C\) در ناحیهٔ 3 و نقطهٔ \(\Large D\) در ناحیهٔ 4 قرار دارد.
مثال از مختصات ریاضی هفتم
مثال 2: بدون مشخص کردن نقاط \(\Large A=\begin{bmatrix} -1 \\ -5 \end{bmatrix}\) و \(\Large B=\begin{bmatrix} 3 \\ -7 \end{bmatrix}\) در صفحه، تعیین کنید هر کدام در کدام ناحیه از صفحه قرار دارند.
حل: طول نقطهٔ \(\Large A\) برابر با \(\Large -1\) و کوچکتر از صفر است. عرض نقطهٔ \(\Large A\) نیز برابر با \(\Large -5\) و کوچکتر از صفر است. بنابراین، نقطهٔ \(\Large A\) در ناحیهٔ سوم قرار دارد. نقطهٔ \(\Large B\) نیز، از آنجاییکه طولی برابر با \(\Large 3\) و بزرگتر از صفر و عرضی برابر با \(\Large -7\) و کوچکتر از صفر دارد، در ناحیهٔ چهارم قرار میگیرد.
مختصات بردار
میتوان بردارها را مانند نقاط، با استفاده از مختصاتشان نمایش داد. برای این کار میتوان طول نقطهٔ انتها منهای نقطهٔ ابتدای بردار را به عنوان طول بردار و عرض نقطهٔ انتها منهای نقطهٔ ابتدای بردار را به عنوان عرض آن در نظر گرفت. برای اینکه بهتر متوجه شوید، بردار \(\Large \overrightarrow{AB}\) در شکل زیر را در نظر بگیرید:
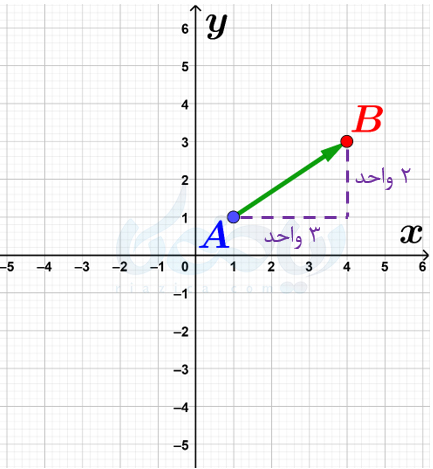
اگر بردار \(\Large \overrightarrow{AB}\) را به صورت یک حرکت از نقطهٔ \(\Large A\) به نقطهٔ \(\Large B\) در نظر بگیریم، میتوانیم بگوییم 3 واحد در راستای محور \(\Large x\) و 2 واحد در راستای محور \(\Large y\) جلو رفتهایم. بنابراین میتوانیم بردار \(\Large \overrightarrow{AB}\) را به صورت زیر نمایش دهیم:
\(\LARGE \overrightarrow{AB}=B-A=\begin{bmatrix} 3\\ 2 \end{bmatrix}\)
به عبارت دیگر، اگر به طول نقطهٔ \(\Large A=\begin{bmatrix} 1\\ 1 \end{bmatrix}\) که برابر با \(\Large 1\) است، 3 واحد اضافه کنیم، طول نقطهٔ \(\Large B=\begin{bmatrix} 4\\ 3 \end{bmatrix}\) که برابر با \(\Large 4\) است به دست می آید. همچنین، اگر به عرض نقطهٔ \(\Large A=\begin{bmatrix} 1\\ 1 \end{bmatrix}\) که برابر با \(\Large 1\) است، 2 واحد اضافه کنیم، عرض نقطهٔ \(\Large B=\begin{bmatrix} 4\\ 3 \end{bmatrix}\) که برابر با \(\Large 3\) است حاصل میشود.
مثال از مختصات ریاضی هفتم
مثال 3: مختصات بردارهای \(\Large \overrightarrow{AB}\) و \(\Large \overrightarrow{CD}\) را که در شکل زیر مشخص شدهاند، بنویسید.
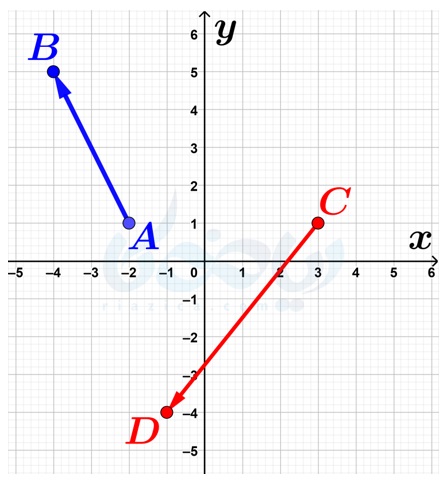
حل: میتوانیم برای درک آسانتر، تعداد واحدی را که در هر بردار در جهت محورها حرکت میکنیم، به صورت زیر روی شکل مشخص کنیم:
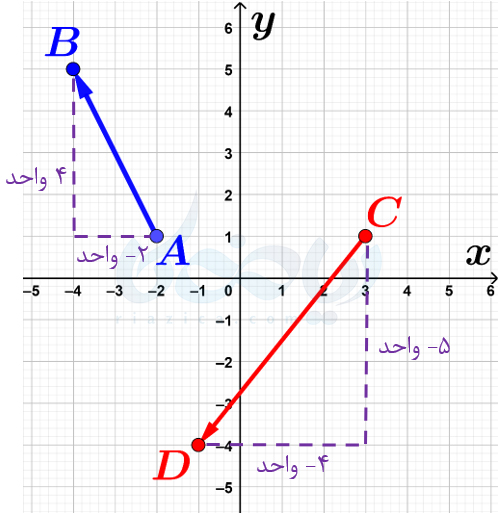
ابتدا مختصات نقاط \(\Large A\) و \(\Large B\) را مینویسیم:
\(\LARGE A=\begin{bmatrix} -2\\ 1 \end{bmatrix}\)
\(\LARGE B=\begin{bmatrix} -4\\ 5 \end{bmatrix}\)
پس اگر \(\Large -2\) واحد به طول نقطهٔ \(\Large A\) و \(\Large 4\) واحد به عرض نقطهٔ \(\Large A\) اضافه کنیم، مختصات نقطهٔ \(\Large B\) به دست میآید. در نتیجه مختصات بردار \(\Large \overrightarrow{AB}\) به صورت زیر است:
\(\LARGE \overrightarrow{AB}=B-A=\begin{bmatrix} -2\\ 4 \end{bmatrix}\)
برای به دست آوردن مختصات بردار \(\Large \overrightarrow{CD}\) نیز ابتدا مختصات نقاط \(\Large C\) و \(\Large D\) را تعیین میکنیم:
\(\LARGE C=\begin{bmatrix} 3\\ 1 \end{bmatrix}\)
\(\LARGE D=\begin{bmatrix} -1\\ -4 \end{bmatrix}\)
بنابراین اگر \(\Large -4\) واحد به طول نقطهٔ \(\Large C\) و \(\Large -5\) واحد به عرض نقطهٔ \(\Large C\) اضافه کنیم، مختصات نقطهٔ \(\Large D\) به دست میآید. در نتیجه مختصات بردار \(\Large \overrightarrow{CD}\) به صورت زیر است:
\(\LARGE \overrightarrow{CD}=D-C=\begin{bmatrix} -4\\ -5\end{bmatrix}\)
مثال از مختصات ریاضی هفتم
مثال 4: ابتدای یک بردار، نقطهٔ \(\Large A=\begin{bmatrix} -3\\ -8 \end{bmatrix}\) و انتهای آن، نقطهٔ \(\Large B=\begin{bmatrix} -2\\ 6 \end{bmatrix}\) است. بدون رسم بردار، مختصات آن را تعیین کنید.
حل: همان طور که گفتیم، برای تعیین مختصات هر برداری باید طول انتهای آن را منهای طول ابتدای آن کرده و عرض انتهای آن را منهای عرض ابتدای آن کنیم. به این صورت، مختصات بردار تعیین میشود. به عبارت دیگر، کافی است ببینیم چه اعدادی را باید به طول و عرض نقطهٔ ابتدای بردار اضافه کرد تا طول و عرض نقطهٔ انتهای آن به دست بیاید. اگر به طول نقطهٔ \(\Large A\) مقدار \(\Large 1\) واحد اضافه کرده و به عرض آن \(\Large 14\) واحد اضافه کنیم، طول و عرض نقطهٔ \(\Large B\) به دست میآید. بنابراین مختصات بردار \(\Large \overrightarrow{AB}\) به صورت زیر است:
\(\LARGE \overrightarrow{AB}=B-A=\begin{bmatrix} 1\\ 14 \end{bmatrix}\)
مثال از مختصات ریاضی هفتم
مثال 5: قرینهٔ بردار \(\Large \overrightarrow{AB}\) را نسبت به محور عرضها رسم کرده، سپس مختصات بردار قرینه را تعیین کنید.
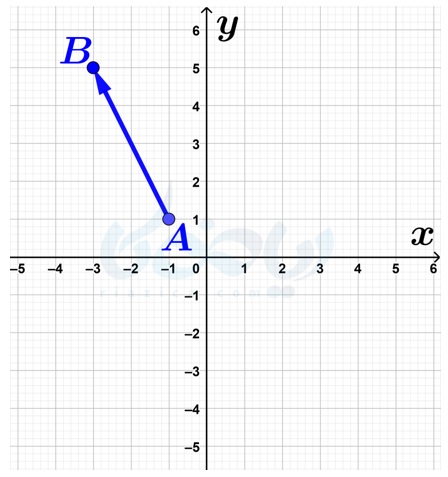
حل: همان طور که در درسنامهٔ تبدیلات هندسی ریاضی هفتم خواندید، برای پیدا کردن قرینهٔ محوری یک پارهخط کافی است از نقاط ابتدا وانتهای آن به خطی که قرار است قرینه را نسبت به آن به دست آوریم، عمود کرده و به اندازهٔ طول عمود، آن را ادامه دهیم. بنابراین، برای تعیین قرینهٔ بردار \(\Large \overrightarrow{AB}\)، قرینهٔ نقاط \(\Large A\) و \(\Large B\) را به دست آورده و بردار \(\Large \overrightarrow{A’B’}\) را رسم میکنیم:
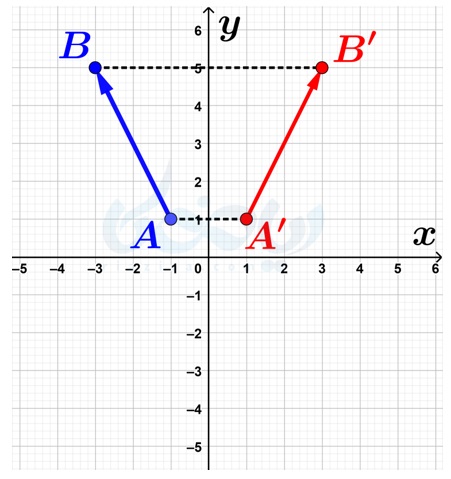
به این ترتیب، مختصات نقاط \(\Large A’\) و \(\Large B’\) به صورت زیر است:
\(\LARGE A’=\begin{bmatrix} 1\\ 1 \end{bmatrix}\)
\(\LARGE B’=\begin{bmatrix} 3\\ 5 \end{bmatrix}\)
همان طور که میبینید، مختصات نقاط \(\Large A’\) و \(\Large B’\) از قرینه کردن طول نقاط \(\Large A\) و \(\Large B\) و ثابت نگه داشتن عرض آنها به دست میآید. مانند قسمتهای قبل، برای تعیین مختصات بردار \(\Large \overrightarrow{A’B’}\) کافی است ببینیم با اضافه کردن چه اعدادی به مختصات نقطهٔ \(\Large A’\)، مختصات نقطهٔ \(\Large B’\) به دست میآید. اگر \(\Large 2\) واحد به طول نقطهٔ \(\Large A’\) و \(\Large 4\) واحد به عرض آن اضافه کنیم، مختصات نقطهٔ \(\Large B’\) به دست می آید. بنابراین مختصات بردار \(\Large \overrightarrow{A’B’}\) به صورت زیر است:
\(\LARGE \overrightarrow{A’B’}=B’-A’=\begin{bmatrix} 2\\ 4 \end{bmatrix}\)
برای درک بهتر این مطلب پستهای پاره خط جهت دار و بردارهای مساوی وقرینه رو حتما بخونید و در ادامه پست بردار انتقال رو مطالعه کنید و حواست باشه ما تمام درسهای ریاضی پایه هفتم رو به طور کامل برات تدریس کردیم حتما اونها رو هم مطالعه کن
زنگ آخر کلاس مختصات ریاضی هفتم
در درسنامهای که از ریاضی هفتم خواندیم، ابتدا نمایش نقاط در دستگاه مختصات را مرور کردیم. سپس، صفحه را با استفاده از محورها به چهار ناحیه تقسیم کرده و ویژگی هر ناحیه را بیان کردیم. در انتها نیز، به چگونگی تعیین مختصات یک بردار پرداختیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مختصات ریاضی هفتم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





ممنون از شما من در به دست آوردن مختصات خط کمی مشکل داشتم کامل متوجه شدم.
ریاضی بهترین درس است.
با سلام پاحترام
خدا رو شکر که مورد استفاده شما قرار گرفته وواقعا درس ریاضی رو اگه توجه کنیم جزو زیباترین درسهایت
سلام.خسته نباشید عالی بود.فقط قسمت(حل: میتوانیم برای درک آسانتر، تعداد واحدی را که در هر بردار در جهت محورها حرکت میکنیم، به صورت زیر روی شکل مشخص کنیم:) برای بدست اوردن مختصات سی دی اشتباه کردید و بجای اینکه اول از طول شروع به حرکت کنید از عرض شروع به حرکت کردید.
با سلام دوست عزیز
فرقی نمیکنه فقط باید موقع نوشتن مختصات اول طول رو بنویسیم
فک کنم به مغزت فشار اوردی دوست نوشتی پوست 🙂 :):):):)
با سلام
شا به بزرگواری خودتون ببخشید
عالی
با سلام
ممنون از لطف شما
عالی بود فردا امتحان ریاضی دارم ببینم چند میارم
عالی بود من مشکلم حل شد
با سلام وادب
ممنون از لطف شما
سلام خیلی ممنونم من بهتر یاد گرفتم ممنون از دبیر خوب ریاضیکا اما یه سوال میشه به من یه راه حل بدین برای اینکه راحت تر حفظ کنم چه قسمتی تو محورمنفیه چه قسمتی مثبت.
با سلام دوست عزیز
ریاضی رو از چپ به راست می نویسیم اعداد هم روی محور از چپ به راست بیشتر میشن اعداد منفی سمت چپ مثبت سمت راست
نمیدونم
سلام خیلی ممنونم من بهتر یاد گرفتم ممنون از دبیر خوب ریاضیکا اما یه سوال میشه به من یه راه حل بدین برای اینکه راحت تر حفظ کنم چه قسمتی تو محورمنفیه چه قسمتی مثبت.
خیلی زیاد معلوم نیس
با سلام
یعنی تو گوشی خوانا نیست؟
سلام من سما هستم و این خوب درس یاد نمیدهد
و مفهـومـ نـیـسـ
🥹😭⛓️🥺😐😐😐😐😐😐
سلام دوست عزیز دقیقا کجا مفهوم نیست راهنمایی کنید برای بهبود سایت
ممنون از زحمات شما
سلام عالی بود👌👌👌👌👌💋💋💋💋💋
با سلام خوشحالیم که برای شما مفید بوده
سلام عالی بود👌👌👌👌👌💋💋💋💋💋
اگر بردار ab منفی ۳ و ۳ باشد و بردار bc ۴ و ۱ باشد بردار acرا رسم کنید