کوچکترین مضرب مشترک ریاضی هفتم ❎🔑 – ک.م.م پیدا کن!

در درسنامهٔ کوچکترین مضرب مشترک ریاضی هفتم ابتدا مضرب‌های طبیعی و صحیح را بررسی می‌کنیم. در ادامه، مفهوم کوچکترین مضرب مشترک (ک.م.م)  را توضیح داده و نحوهٔ به دست آوردن آن را بررسی می‌کنیم. در آخر نیز، کاربرد محاسبهٔ ک.م.م در به دست آوردن مخرج مشترک کسرها را مرور می‌کنیم. امیدواریم تا با مطالعهٔ این درسنامه و حل مثال‌های آن، مشکلی در درک مبحث کوچکترین مضرب مشترک ریاضی هفتم نداشته باشید.

---

---

مضرب‌های طبیعی و صحیح

مضرب‌های صحیح یک عدد از ضرب آن عدد در اعداد صحیح به دست می‌آیند. مثلاً برخی از مضارب صحیح عدد \(\Large 2\) را در زیر نوشته‌ایم:

طبیعتاً از آنجاییکه نامتناهی عدد منفی و نامتناهی عدد مثبت داریم، مضارب صحیح اعداد از هر دو طرف ادامه دارد. علامت \(\Large \dots\) در بالا نیز به همین معناست. به همین صورت می‌توانیم مضارب صحیح دیگر اعداد را نیز به دست آوریم. برای تمرین بیشتر، برخی از مضارب صحیح عدد \(\Large 5\) را نیز به دست آورده‌ایم:

مضارب طبیعی یک عدد نیز از ضرب آن عدد در اعداد طبیعی به دست می‌آیند. مثلاً مضارب طبیعی عدد \(\Large 3\)، به صورت زیر به دست می‌آیند:

مضارب طبیعی یک عدد را به اختصار، مضارب آن عدد می‌گوییم. در ادامهٔ درسنامهٔ کوچکترین مضرب مشترک ریاضی هفتم برخی از مضارب اعداد \(\Large 4\) و \(\Large 7\) را نشان داده‌ایم:

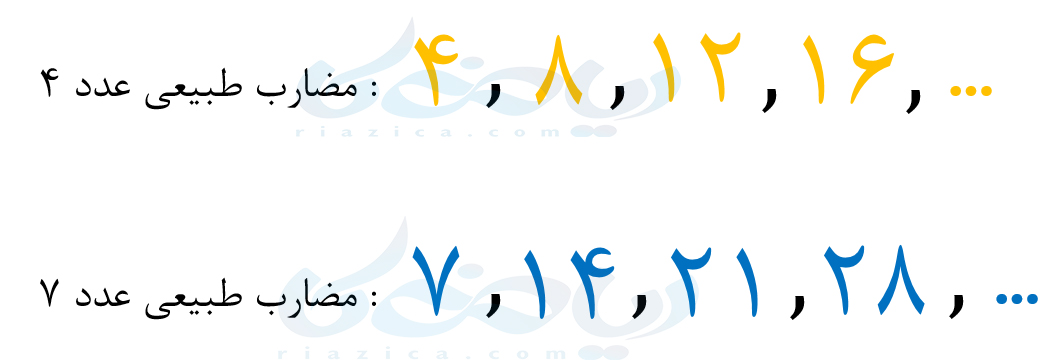
کوچکترین مضرب مشترک طبیعی دو عدد

در صورتی که دو یا چند عدد، تعدادی مضرب مشترک طبیعی داشته باشند، کوچکترینِ آن‌ها، کوچکترین مضرب مشترک یا به اختصار ک.م.م نامیده می‌شود. مثلاً تعدادی از مضارب عدد \(\Large 2\) و عدد \(\Large 3\) را نوشته‌ایم:

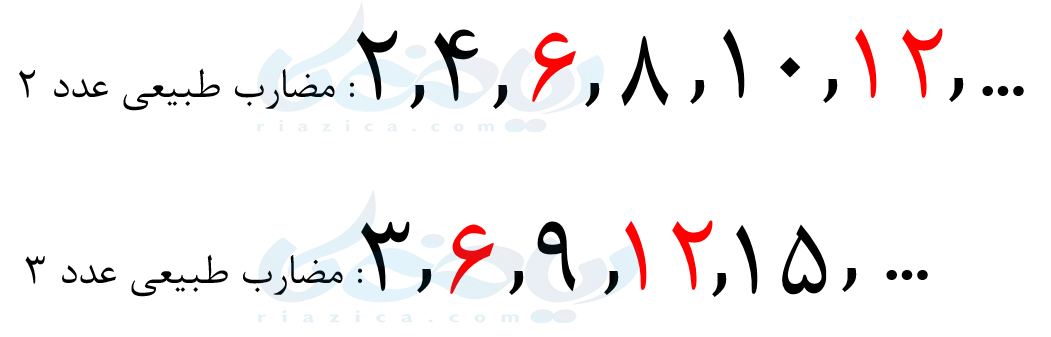
همان‌طور که در بالا می‌بینید، مضاربی که بین \(\Large 2\) و \(\Large 3\) مشترک هستند را با رنگ قرمز نشان داده‌ایم. کوچکترین مضرب مشترک \(\Large 2\) و \(\Large 3\)، عدد \(\Large 6\) است. برای نشان دادن کوچکترین مضرب مشترک (ک.م.م) دو عدد \(\Large a\) و \(\Large b\)، از نماد \(\Large [a, b]\) استفاده می‌کنیم. بنابراین برای دو عدد \(\Large 2\) و \(\Large 3\) می‌توانیم بنویسیم:

\(\LARGE [2, 3]=6 \)

هر دو عدد طبیعی دلخواه \(\Large a\) و \(\Large b\)، حداقل یک مضرب مشترک دارند که همان \(\Large a \times b\) است. بنابراین در هر صورتی برای هر دو عدد دلخواه، کوچکترین مضرب مشترک وجود دارد (البته به طور دقیق تر، برای اثبات این موضوع لازم است که از اصل خوش ترتیبی اعداد طبیعی استفاده کنیم. در صورتی که علاقه‌مندید در مورد آن مطالعه کنید). در ادامۀ درسنامۀ کوچکترین مضرب مشترک ریاضی هفتم دو روش برای یافتن ک.م.م  را معرفی خواهیم کرد.

روش‌های به دست آوردن کوچکترین مضرب مشترک

برای پیدا کردن ک.م.م دو عدد می‌توانیم از یکی از روش‌های زیر استفاده کنیم:

1. تعدادی از مضارب طبیعی دو عدد را می‌نویسیم. مضاربی که بین دو عدد مشترک است را در نظر می‌گیریم. کوچکترینشان، ک.م.م دو عدد است.
2. دو عدد را به حاصل ضرب شمارنده‌های اول تجزیه می‌کنیم. از هر یک از شمارنده‌های غیر مشترک، بیشترین تعدادشان در یک عدد را در نظر می‌گیریم. ک.م.م دو عدد برابر خواهد بود با حاصل ضرب شمارنده‌های مشترک با بیشترین تکرار از هر یک از شمارنده‌های غیر مشترک در یک عدد. البته این جمله دقیق نیست؛ اما چون هنوز با مفهوم توان آشنا نشده‌اید، مجبوریم از این عبارت استفاده کنیم. می‌توان خیلی راحت تر با استفاده از مفهوم توان، این روش را به این صورت بیان کرد: ک.م.م دو عدد برابر است با حاصل ضرب شمارنده‌های مشترک با بیشترین توان ضرب در شمارنده‌های غیر مشترک.

برای پیدا کردن ک.م.م تعداد بیشتری از اعداد نیز از همین روش استفاده می‌کنیم. برای اینکه استفاده از هر دو روش را ببینید، از هر کدام از آن‌ها در دو قسمت جداگانه از درسنامۀ کوچکترین مضرب مشترک ریاضی هفتم تعدادی مثال حل می‌کنیم.

پیدا کردن ک.م.م با نوشتن مضارب

مثال 1: حاصل \(\Large [6, 9] \) را با نوشتن مضارب طبیعی پیدا کنید.

حل: نمی‌توانیم همۀ مضارب طبیعی یک عدد را بنویسیم؛ زیرا تعداد آن نامتناهی است. اما تعدادی از مضارب طبیعی دو عدد را می‌نویسیم تا جایی که بتوانیم کوچکترین مضرب مشترک دو عدد را پیدا کنیم. مضارب طبیعی اعداد \(\Large 6\) و \(\Large 9\) به صورت زیر هستند: 

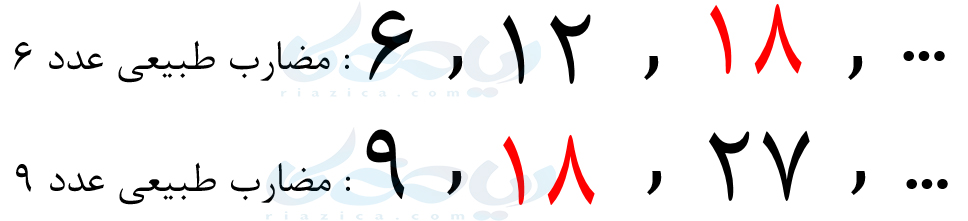
مضارب مشترک دو عدد \(\Large 6\) و \(\Large 9\) را با رنگ قرمز مشخص کرده‌ایم. همان طور که می‌بینید، عدد \(\Large 18\)، کوچکترین عدد قرمز رنگ است؛ یعنی کوچکترین مضرب مشترک دو عدد \(\Large 6\) و \(\Large 9\) است. بنابراین داریم:

\(\LARGE [6, 9]=18\)

به مثال بعدی از درسنامۀ کوچکترین مضرب مشترک ریاضی هفتم توجه کنید.

مثال 2: حاصل \(\Large [12, 4, 6] \) را با نوشتن مضارب طبیعی پیدا کنید.

حل: همان طور که گفتیم، برای پیدا کردن ک.م.م بیشتر از دو عدد نیز می‌توانیم از روش‌هایی که گفتیم استفاده کنیم. مضارب اعداد \(\Large 4\) و \(\Large 6\) و \(\Large 12\) به صورت زیر هستند:

مضارب مشترک سه عدد را با رنگ قرمز مشخص کرده‌ایم. کوچکترین مضرب مشترک سه عدد \(\Large 4\) و \(\Large 6\) و \(\Large 12\)، عدد \(\Large 12\) است. بنابراین داریم:

\(\LARGE [12, 4, 6]=12\)

در قسمت بعدی از درسنامۀ کوچکترین مضرب مشترک ریاضی هفتم دو مثال از روش دوم یافتن ک.م.م حل خواهیم کرد.

---

---

پیدا کردن ک.م.م با تجزیۀ اعداد

مثال 3: حاصل \(\Large [18, 6] \) را با استفاده از تجزیۀ اعداد پیدا کنید.

حل:  در درسنامۀ شمارنده اول، روش تجزیۀ اعداد و پیدا کردن شمارنده‌های اول یک عدد را آموختیم. اعداد \(\Large 18\) و \(\Large 6\) را به حاصل ضرب شمارنده‌های اول تجزیه می‌کنیم:

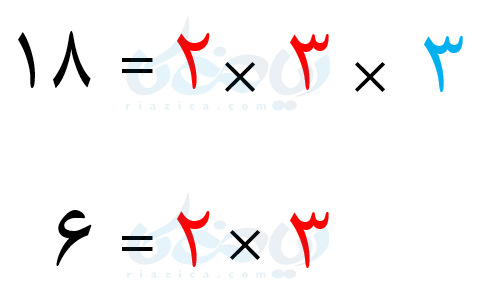
شمارنده‌های اول مشترک دو عدد را با رنگ قرمز نشان داده‌ایم. طبق روش دوم، ک.م.م دو عدد برابر است با با حاصل ضرب شمارنده‌های مشترک در شمارنده‌های غیر مشترک. قسمت مشترک در دو عدد، \(\Large 2 \times 3\) است. اما یک عدد \(\Large 3\) در \(\Large 18\) اضافی می‌آید و غیر مشترک محسوب می‌شود. بنابراین داریم:

\(\LARGE [18, 6]=2 \times 3 \times 3=18\)

استفاده از مفهوم توان

همین مثال (مثال 3) از درسنامۀ کوچکترین مضرب مشترک ریاضی هفتم را می‌توان با استفاده از مفهوم توان که در درس‌ تعریف توان ریاضی هفتم می‌خوانید به این صورت حل کرد:

ابتدا اعداد \(\Large 6\) و \(\Large 18\) را به صورت زیر تجزیه می کنیم:

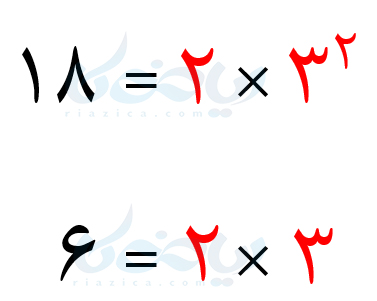
شمارندۀ \(\Large 2\) بین هر دو عدد مشترک است و بیشترین توان آن برابر با \(\Large 1\) است. شمارندۀ \(\Large 3\) نیز بین هر دو عدد مشترک است و بیشترین توان آن برابر با \(\Large 2\) است. بنابراین ک.م.م دو عدد \(\Large 6\) و \(\Large 18\) برابر است با:

\(\LARGE [18, 6]=2 \times 3^2=18\)

به مثال بعدی از درسنامۀ کوچکترین مضرب مشترک ریاضی هفتم توجه کنید.

مثال 4: حاصل \(\Large [12, 18, 9] \) را با استفاده از تجزیۀ اعداد پیدا کنید.

حل: از روش تجزیۀ اعداد برای پیدا کردن ک.م.م بیش از دو عدد نیز می‌توان استفاده کرد. هر یک از سه عدد را به صورت حاصل ضرب شمارنده‌های اول می‌نویسیم:

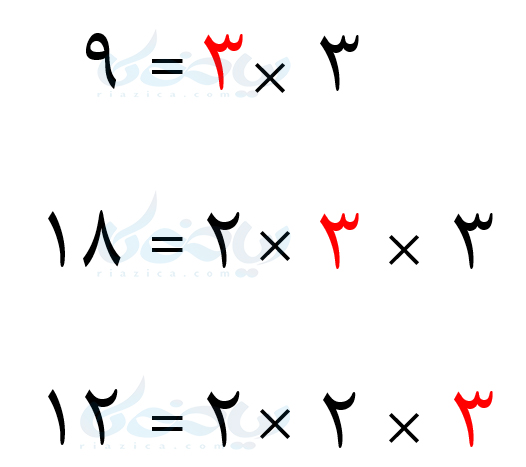
شمارنده‌های مشترک را با رنگ قرمز و شمارنده‌های غیر مشترک را با رنگ سیاه نشان داده‌ایم. قسمت مشترک حاصل ضرب بین سه عدد، عدد \(\Large 3\) است. دو عامل غیر مشترک \(\Large 2\) و \(\Large 3\) باقی می‌مانند. بیشترین تکرار \(\Large 2\) غیر مشترک، در \(\Large 12\) قرار دارد و تعداد تکرار آن برابر با دو است. بیشترین تکرار \(\Large 3\) غیر مشترک نیز برابر با یک است. بنابراین حاصل ضرب عوامل غیر مشترک با بیشترین تکرار هر یک بین اعداد برابر است با \(\Large 2 \times 2 \times 3\). بنابراین داریم:

\(\Large [9, 18, 12]=3 \times 2 \times 2 \times 3=36\)

استفاده از مفهوم توان

همین مثال (مثال 4) از درسنامۀ کوچکترین مضرب مشترک ریاضی هفتم را می‌توان با استفاده از مفهوم توان که در درس‌ تعریف توان ریاضی هفتمبا آن آشنا می‌شوید، به صورت زیر حل کرد:

ابتدا سه عدد \(\Large 9\) و \(\Large 18\) و \(\Large 12\) را به صورت زیر تجزیه می‌کنیم:

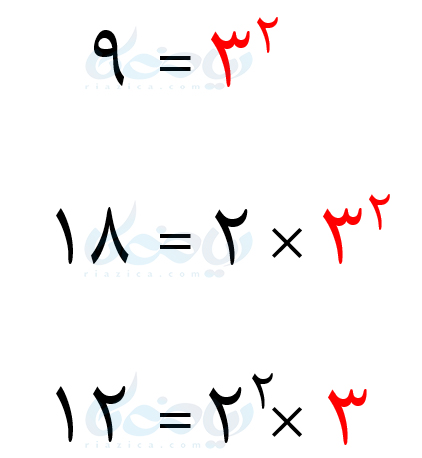
شمارندۀ \(\Large 3\) بین هر سه عدد مشترک است و بیشترین توان آن برابر با \(\Large 2\) است. شمارندۀ \(\Large 2\) تنها بین دو عدد \(\Large 18\) و \(\Large 12\) مشترک است و بیشترین توان آن برابر با \(\Large 2\) است. بنابراین ک.م.م سه عدد \(\Large 9\) و \(\Large 18\) و \(\Large 12\) برابر است با:

\(\Large [9, 18, 12]=3^2 \times 2^2=36\)

پس به طور خلاصه میشه گفت ک.م.م میشه حاصلضرب شمارنده های مشترک وغیر مشترک با توان بیشتر.

به قسمت بعدی از درسنامۀ کوچکترین مضرب مشترک ریاضی هفتم توجه کنید.

نکات کلیدی در مورد ک.م.م اعداد

۱-ک.م.م دوعدد اول برابر است با حاصلضرب آنها .مثال: \(\LARGE [3, 11]=33\)

۲-ک.م.م هر عدد با یک می شود خود آن عدد. \(\LARGE [1, n]=n\)

۳- ک.م.م هر عدد با خودش می شود خود آن عدد. \(\LARGE [n, n]=n\)

۴- اگر دو عدد به هم بخش پذیر باشند ک.م.م آنها می شود عدد بزرگتر. مثال: \(\LARGE [6, 3]=6\)

۵- ب.م.م دوعدد شمارنده ک.م.م دوعدد است.

۶- حاصلضرب دوعدد برابر حاصلضرب ب.م.م وک.م.م دو عدد می باشد.

۷- ک.م.م دو عدد متوالی بربر است با حاصلضرب آنها. مثال: \(\LARGE [9, 10]=90\)

کاربرد ک.م.م در محاسبۀ مخرج مشترک

زمانی که می‌خواهیم چند کسر را با یکدیگر جمع و یا از یکدیگر تفریق کنیم، لازم است که مخرج کسرها را یکی کرده تا عملیات جمع و تفریق را روی صورت کسرها انجام دهیم. از آنجاییکه ک.م.م مخرج چند کسر، مضرب مشترک آن‌هاست، در صورتی که مخرج هر کسر را در یک عدد مشخص ضرب کنیم، مخرج هر کسر برابر با ک.م.م مخرج‌ها خواهد شد. از طرفی چون ک.م.م، کوچکترین مضرب مشترک است، مقدار مخرج مشترک، کوچکترین عدد طبیعی ممکن خواهد بود. بنابراین کار ما در محاسبه آسان‌تر می‌شود. برای اینکه بهتر متوجه شوید، به مثال‌ بعدی از درسنامۀ کوچکترین مضرب مشترک ریاضی هفتم توجه کنید.

مثال از کاربرد ک.م.م در محاسبۀ مخرج مشترک

مثال 5: حاصل عبارت \(\Large \frac{3}{16}+\frac{5}{18}\) را با محاسبۀ ک.م.م مخرج کسرها به دست آورید.

حل: ابتدا باید مخرج مشترک را محاسبه کنیم. مطابق با خواستۀ مسئله، مخرج مشترک دو کسر را با استفاده از محاسبۀ ک.م.م مخرج‌ها محاسبه می‌کنیم. تجزیۀ اعداد \(\Large 16\) و \(\Large 18\) به صورت زیر است:

قسمت مشترک بین دو عدد که با رنگ قرمز مشخص شده است، برابر است با عدد \(\Large 2\). حاصل ضرب شمارنده‌های غیر مشترک با بیشترین تکرار هر یک بین دو عدد برابر است با \(\Large 2 \times 2 \times 2 \times 3 \times 3\). بنابراین داریم: 

\(\Large [16, 18]=2 \times 2 \times 2 \times 2 \times 3 \times 3=144 \)

\(\Large =144 \)

بنابراین مخرج مشترک دو کسر برابر است با \(\Large 144\). مخرج کسر \(\Large \frac{3}{16}\) در \(\Large 9\) ضرب شده، بنابراین صورت آن نیز در \(\Large 9\) ضرب می‌شود. مخرج کسر \(\Large \frac{5}{18}\) در \(\Large 8\) ضرب شده، بنابراین صورت آن نیز در \(\Large 8\) ضرب می‌شود. بنابراین داریم:

\(\LARGE \frac{3}{16}+\frac{5}{18}=\frac{3 \times 9}{144}+\frac{5 \times 8}{144}\)

\(\LARGE =\frac{27}{144}+\frac{40}{144}\)

\(\LARGE =\frac{67}{144}\)

استفاده از ک.م.م در حل مسائل

گاهی در صورت مسئله، به صورت مستقیم، محاسبۀ ک.م.م دو عدد را از ما نمی‌خواهند. اما برای حل مسئله لازم است تا ک.م.م دو یا چند عدد را محاسبه کنیم. طبیعتاً زمانی به محاسبۀ ک.م.م چند عدد نیاز داریم که  از بین مضارب آن‌ها به دنبال کوچکترینشان هستیم. به مثال زیر از درسنامۀ کوچکترین مضرب مشترک ریاضی هفتم توجه کنید.

مثال 6: در یک مسابقۀ دو‌‌و‌میدانی، شرکت‌کنندۀ \(\Large A\) هر \(\Large 18\) ثانیه و شرکت کنندۀ \(\Large B\) هر \(\Large 45\) ثانیه، یک دور کامل میدان را طی می‌کنند. بعد از چند ثانیه از شروع مسابقه، هر دو شرکت کننده برای اولین بار از کنار یکدیگر در نقطۀ شروع می‌گذرند؟

حل: شرکت کنندۀ \(\Large A\) در مضارب عدد \(\Large 18\) از نقطۀ شروع می‌گذرد. شرکت کنندۀ \(\Large B\) در مضارب \(\Large 45\) از نقطۀ شروع می‌گذرد. بنابراین دو شرکت کننده در مضارب مشترک اعداد \(\Large 18\) و \(\Large 45\) از کنار یکدیگر می‌گذرند. چون در مسئله از ما خواسته شده که چه زمانی برای اولین بار بعد از شروع مسابقه از کنار هم می‌گذرند، باید کوچکترین مضرب مشترک دو عدد \(\Large 18\) و \(\Large 45\) را به دست آوریم. دو عدد را به صورت زیر تجزیه می‌کنیم:

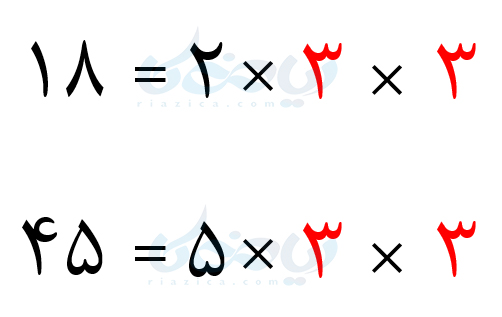
قسمت مشترک بین دو عدد، \(\Large 3 \times 3\) است. حاصل ضرب شمارنده‌های غیر مشترک با بیشترین تکرار در هر یک از دو عدد برابر است با \(\Large 2 \times 5\). بنابراین داریم:

\(\Large [18, 45]=3 \times 3 \times  2 \times 5 =90 \)

بنابراین دو شرکت کننده در ثانیۀ \(\Large 90\) برای اولین بار بعد از شروع مسابقه از کنار یکدیگر عبور می‌کنند.

توصیه میشه قبل از خوندن این پست ،پستهای عدد اول ریاضی هفتم وشمارنده اول ریاضی هفتم و بزرگترین شمارنده مشترک ریاضی هفتم را مطالعه کنید.

زنگ آخر کلاس کوچکترین مضرب مشترک ریاضی هفتم

در این درسنامه از ریاضی هفتم ابتدا ضرایب طبیعی اعداد را بررسی کردیم. دیدیم که بین چند عدد، برخی از ضرایب مشترک هستند. به کوچکترین مضرب مشترک بین آن‌ها، ک.م.م گفته و دو روش برای محاسبۀ آن بیان کردیم. همچنین در انتهای درسنامه دیدیم که از ک.م.م در محاسبۀ مخرج مشترک کسرها و حل برخی از مسائل می‌توان استفاده کرد.

ما در ریاضیکا آماده‌ی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با این مبحث دارید، در دیدگاه‌ها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند ‌داد.

---

---