آموزش ریاضی پایه نهم
همنهشتی مثلث ها نهم 3️⃣🔺 – ۳ حالتشو یادبگیر!
مبحث همنهشتی مثلث ها نهم مروری است بر مطالبی که در سال هشتم خواندید. بنابراین پیشنها میکنیم که اگر درس مثلث های همنهشت پایۀ هشتم را فراموش کردهاید، قبل از مطالعۀ این درسنامه، درسنامۀ مثلث های هم نهشت هشتم را مطالعه کنید. در واقع در این درسنامه تنها سعی داریم حالت های هم نهشتی مثلث ها را به زبان ریاضی بازنویسی کنیم. با مطالعۀ متن درسنامه و حل مثالهای آن، مشکلی در درک این درس نخواهید داشت. با ما همراه باشید.
نتایج همنهشتی دو مثلث
این که در چه حالتهایی دو مثلث، هم نهشت هستند را در قسمتهای بعدی درسنامۀ همنهشتی مثلث ها نهم بررسی میکنیم. اما قبل از آن بهتر است با درسنامه مثلث های هم نهشت مرور کوتاهی کنیم بر پایۀ هشتم و به این سؤال پاسخ دهیم که همنهشتی دو مثلث، چه نتایجی دارد؟ زمانی که دو مثلث، هم نهشت هستند، ضلعها و زاویههای آنها نظیر به نظیر با یکدیگر برابرند. به طور مثال، دو مثلث زیر را در نظر بگیرید:
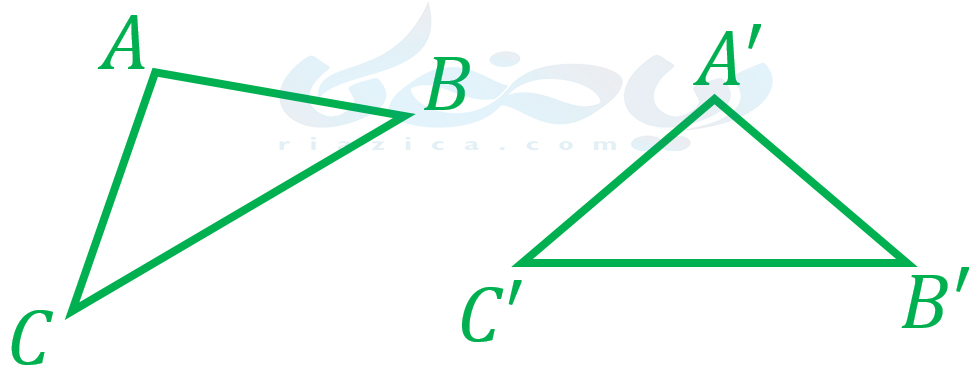
همنهشتی این دو مثلث، برابریهای زیر را نتیجه میدهد:
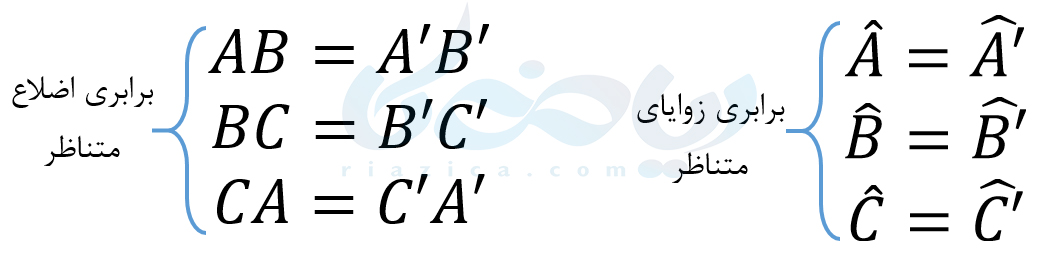
این که کدام ضلع یکی با دیگری برابر است و کدام زاویه از یک مثلث، با زاویۀ دیگر هماندازه است، به فرضیات مسئله و حالتهای همنهشتی بستگی دارد که در ادامه آنها را بررسی خواهیم کرد.
حالتهای مختلف همنهشتی مثلث ها نهم
حال که نتایج حاصل از همنهشتی دو مثلث را مرور کردیم، به بررسی حالتهای مختلفی که به واسطۀ آنها دو مثلث، هم نهشت میشوند، میپردازیم. همانطور که در پایۀ هشتم خواندهاید، سه حالت برای هم نهشتی مثلث ها وجود دارد:
- برابری سه ضلع (ض ض ض)
- برابری دو ضلع و زاویۀ بین (ض ز ض)
- برابری دو زاویه و ضلع بین (ز ض ز)
در ادامۀ درسنامۀ همنهشتی مثلث ها نهم هر حالت را ابتدا به صورت جداگانه و با استفاده از نمادهای ریاضی بازنویسی کرده و سپس مثالهایی از هر حالت حل میکنیم.
برابری سه ضلع (ض ض ض)
در صورتی که سه ضلع یک مثلث با مثلث دیگری برابر باشند، آن دو مثلث با یکدیگر همنهشت هستند. این حالت از هم نهشتی را میتوانیم به صورت زیر نشان دهیم:
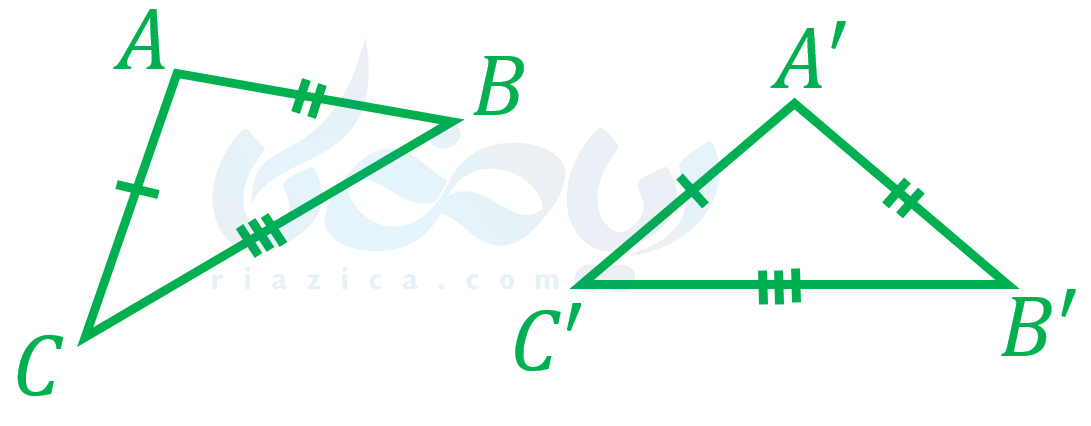
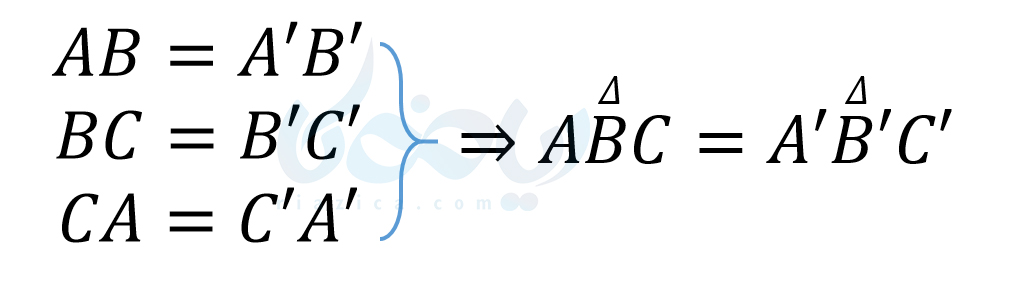
در نتیجۀ این همنهشتی، زوایای دو مثلث نیز، نظیر به نظیر با یکدیگر برابرند. یعنی:
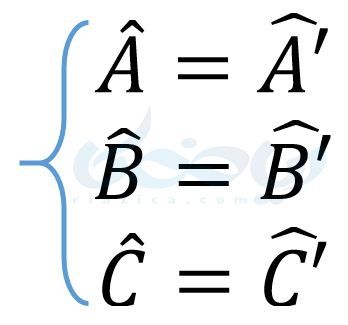
مثال از برابری سه ضلع (ض ض ض)
مثال 1: در شکل زیر، مثلث \(\Large ABC\) متساویالساقین است. \(\Large AM\) نیز میانه است. ثابت کنید \(\Large AM\) نیمساز زاویۀ \(\Large A\) بوده و بر \(\Large BC\) عمود است.
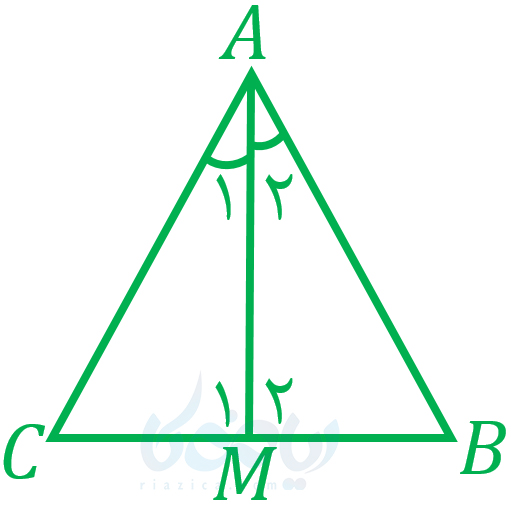
حل: ابتدا ثابت میکنیم مثلث \(\Large ABM\) با مثلث \(\Large ACM\) همنهشت است:

بنابراین در قسمت اول این مثال از درسنامۀ همنهشتی مثلث ها نهم ثابت کردیم مثلث \(\Large ABM\) با مثلث \(\Large ACM\) همنهشت است. حال با توجه به هم نهشتی دو مثلث، نتایج زیر را داریم:
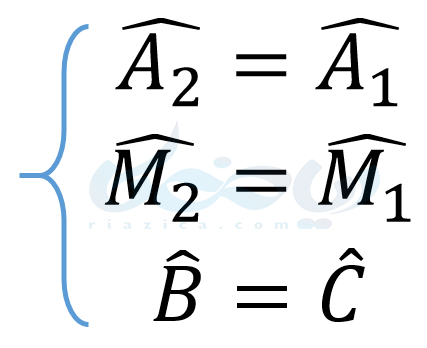
در نتیجه \(\Large AM\) نیمساز زاویۀ \(\Large A\) است. از طرفی به دلیل هم نهشت بودن دو مثلث \(\Large ABM\) و \(\Large ACM\)، زوایای \(\Large M_1\) و \(\Large M_2\) نیز با یکدیگر برابرند. از آنجاییکه زوایای \(\Large M_1\) و \(\Large M_2\) مکمل یکدیگر هستند، نتیجه میگیریم \(\Large M_1=M_2=90^{\circ}\). بنابراین، \(\Large AM\) بر \(\Large BC\) عمود است. به مثال بعدی از درسنامۀ همنهشتی مثلث ها نهم توجه کنید.
مثال از دایره
مثال 2: در شکل زیر، \(\Large AB=CD\) است. ثابت کنید \(\Large \hat{O_1}=\hat{O_2}\).
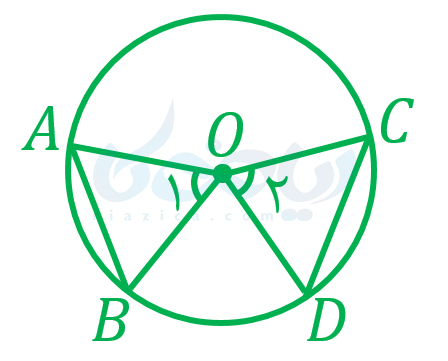
حل: ثابت میکنیم مثلث \(\Large OAB\) با مثلث \(\Large OCD\) همنهشت است:

حال با توجه به هم نهشتی دو مثلث، نتایج زیر را داریم:
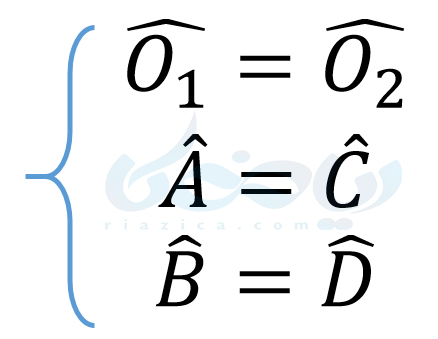
بنابراین ثابت کردیم \(\Large \hat{O_1}=\hat{O_2}\). در قسمت بعدی از درسنامۀ همنهشتی مثلث ها نهم به حالت دوم هم نهشتی مثلث ها میپردازیم.
برابری دو ضلع و زاویۀ بین (ض ز ض)
در صورتی که دو صلع و زاویۀ بین آن در یک مثلث با مثلث دیگری برابر باشند، آن دو مثلث با یکدیگر همنهشت هستند. این حالت از هم نهشتی را میتوانیم به صورت زیر نشان دهیم:
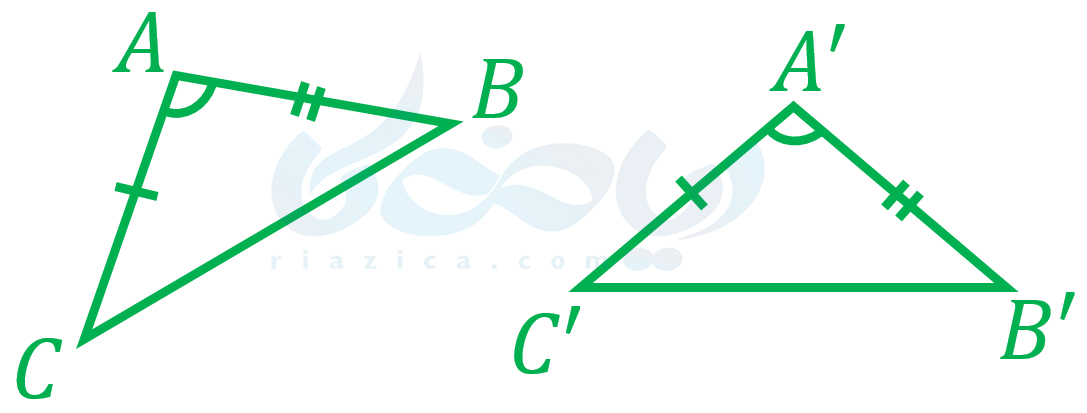
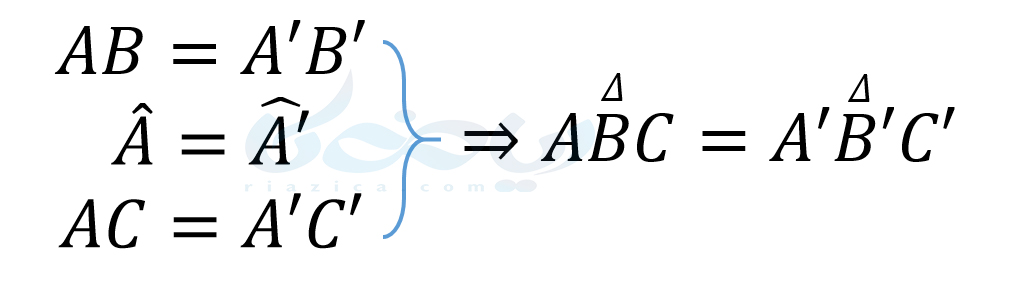
در نتیجۀ این همنهشتی، تساویهای زیر نیز برقرار است:
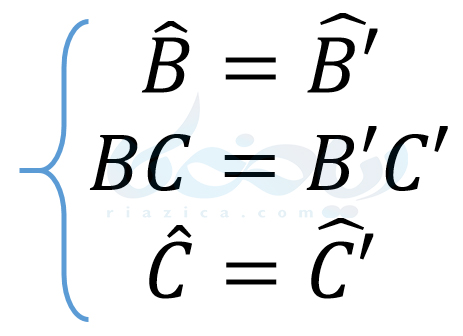
به مثال بعدی از درسنامۀ همنهشتی مثلث ها نهم توجه کنید.
مثال از برابری دو ضلع و زاویۀ بین (ض ز ض)
مثال 3: در شکل زیر، \(\Large ABCD\) مربع است. نقطۀ \(\Large M\) وسط ضلع \(\Large DA\)، نقطۀ \(\Large N\) وسط ضلع \(\Large AB\) و نقطۀ \(\Large P\) وسط ضلع \(\Large BC\) قرار دارد. ثابت کنید \(\Large MN=NP\) است.
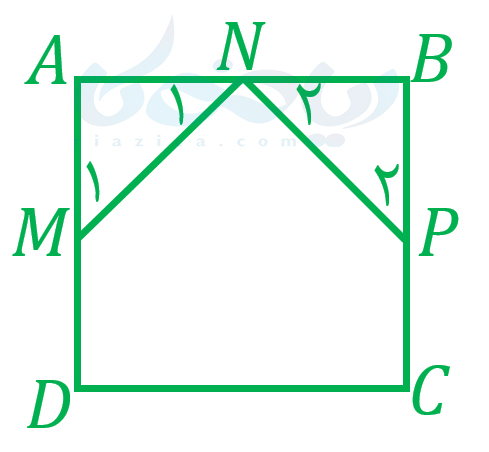
حل: ثابت میکنیم مثلث \(\Large AMN\) با مثلث \(\Large BPN\) همنهشت است:

حال با توجه به هم نهشتی دو مثلث، نتایج زیر را داریم:
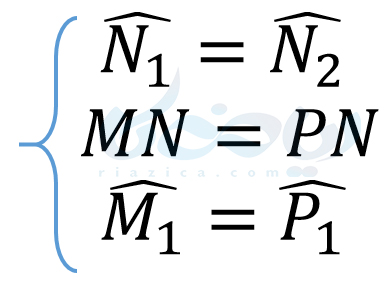
بنابراین ثابت کردیم \(\Large MN=PN\). به مثال بعدی از درسنامۀ همنهشتی مثلث ها نهم توجه کنید
مثال 4: در شکل زیر، مثلث \(\Large ABC\) را در نظر بگیرید. ضلع \(\Large AB\) را به اندازۀ خودش و ضلع \(\Large AC\) را نیز به اندازۀ خودش امتداد دادیم تا مثلث \(\Large AB’C’\) حاصل شود. ثابت کنید مثلث \(\Large ABC\) با مثلث \(\Large AB’C’\) هم نهشت است.
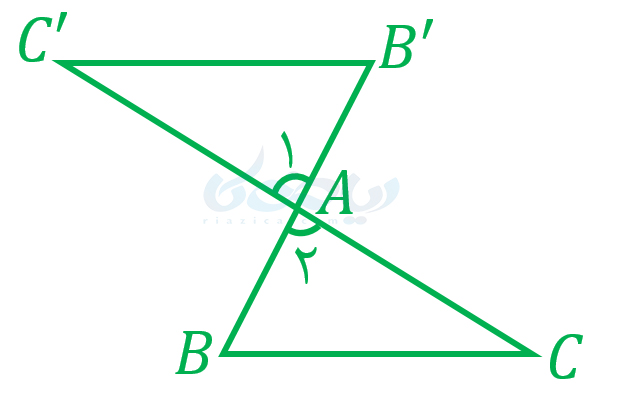
حل:

با توجه به هم نهشتی دو مثلث، نتایج زیر را نیز داریم:
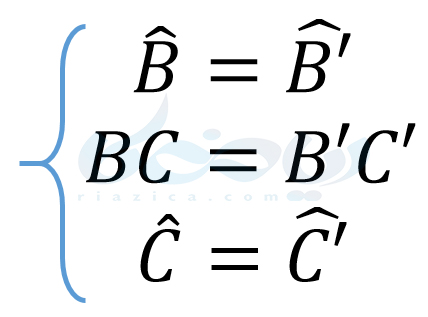
در قسمت بعدی از درسنامۀ همنهشتی مثلث ها نهم به حالت سوم هم نهشتی مثلث ها میپردازیم.
برابری دو زاویه و ضلع بین (ز ض ز)
در صورتی که دو زاویه و ضلع بین آن در یک مثلث با مثلث دیگری برابر باشند، آن دو مثلث با یکدیگر همنهشت هستند. این حالت از هم نهشتی را میتوانیم به صورت زیر نشان دهیم:
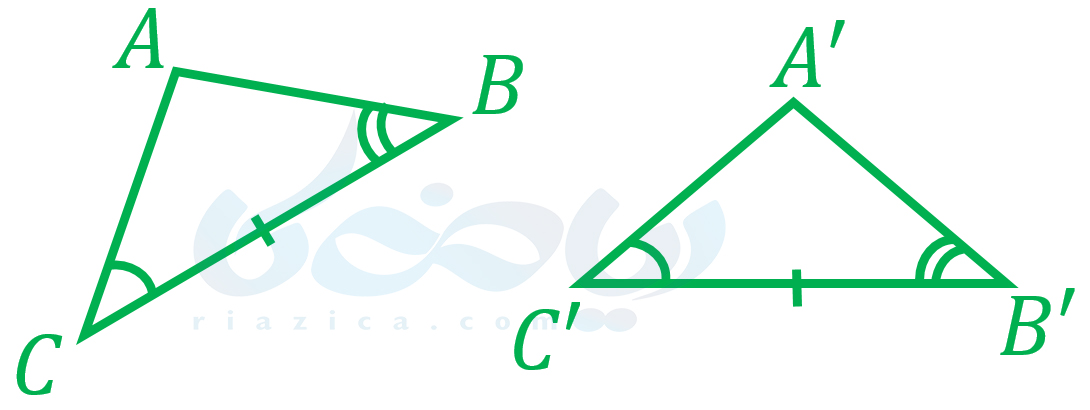
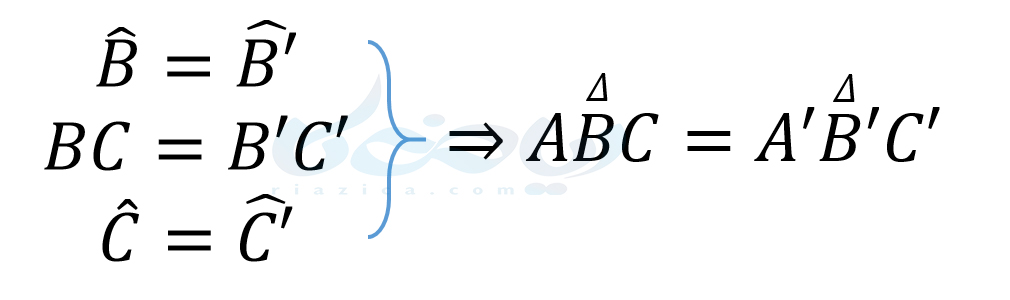
در نتیجۀ این همنهشتی، تساویهای زیر نیز برقرار است:
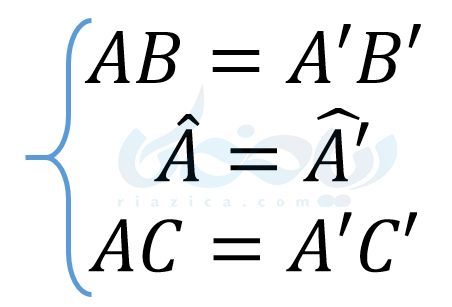
به مثال بعدی از درسنامۀ همنهشتی مثلث ها نهم توجه کنید.
اثبات برابری اضلاع مقابل متوازی الاضلاع
مثال 5: ثابت کنید در هر متوازی الاضلاع، اضلاع مقابل با هم برابرند.
حل: مطابق شکل زیر، یک متوازی الاضلاع دلخواه در نظر گرفته و قطر آن را رسم میکنیم.
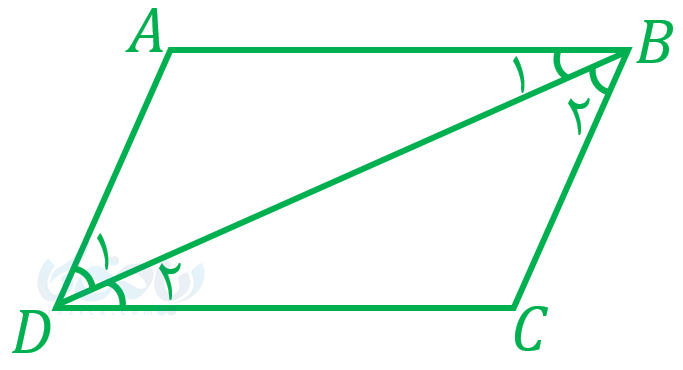
حال ثابت میکنیم دو مثلث \(\Large ABD\) و \(\Large CDB\) با هم هم نهشت هستند:

حال با توجه به هم نهشتی دو مثلث، نتایج زیر را داریم:
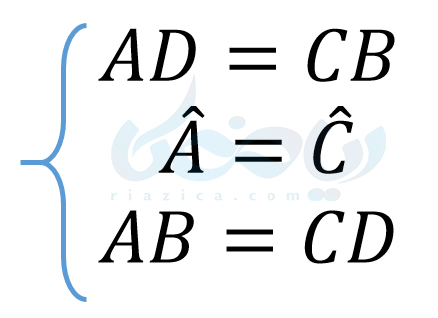
به مثال بعدی از درسنامۀ همنهشتی مثلث ها نهم توجه کنید.
اثبات منصف بودن قطرهای متوازی الاضلاع
مثال 6: ثابت کنید در هر متوازی الاضلاع، قطرها یکدیگر را نصف میکنند.
حل: متوازی الاضلاع دلخواه \(\Large ABCD\) را که در شکل زیر رسم شده است، در نظر بگیرید:
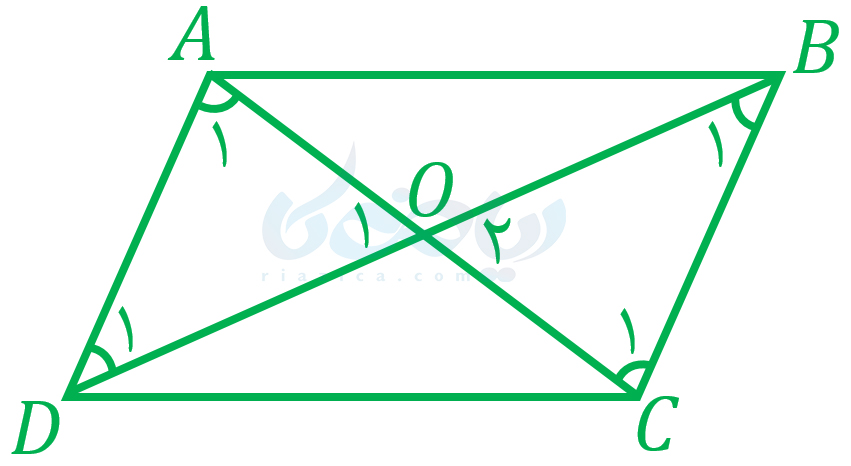
ثابت میکنیم دو مثلث \(\Large AOD\) و \(\Large COB\) با یکدیگر هم نهشت هستند:

حال با توجه به هم نهشتی دو مثلث، نتایج زیر را داریم:
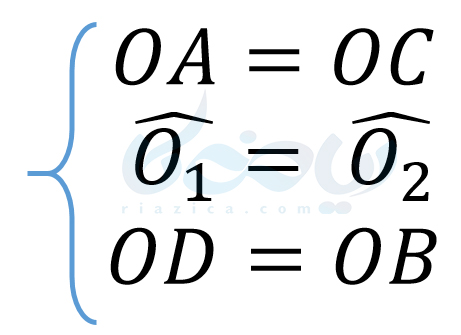
یعنی قطرهای یک متوازی الاضلاع، یکدیگر را نصف میکند.
ویدیو آموزشی از همنهشتی مثلث ها نهم
در این ویدیو آموزشی نمونه سوال از همنهشتی مثلث ها نهم برای شما حل شده است.
زنگ آخر کلاس همنهشتی مثلث ها نهم
همانطور که سال گذشته خواندید، سه حالت برای همنهشتی مثلث ها وجود دارد:
- برابری سه ضلع (ض ض ض)
- برابری دو ضلع و زاویۀ بین (ض ز ض)
- برابری دو زاویه و ضلع بین (ز ض ز)
هر یک از این سه حالت را با استفاده از نمادهای ریاضی بازنویسی کرده و از هریک مثالهایی حل کردیم تا این مبحث را فرا بگیرید.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث همنهشتی مثلث ها نهم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





سلام. چطور میتونیم تشخیص بدیم که دوتا مثلث با چه حالتی باهم همنهشت هستند ؟!
در حالی که حالات هم نهشتی شبیه هم هستند. یعنی دوتا مثلث رو هم میشه باحالت (ض ز ض ) هم نهشت در نظر بگیریم هم با حالت ( ض ض ض ) و هم با حالت ( ز ض ز ) ؟!
ضمن عرض سلام
باید طبق اطلاعات مسئله ببینید که برای تساوی چه ضلعها و زاویههایی دلیل داریم و این دلایل با کدام یک از حالتهای همنهشتی منطبق است.
وای منم همین مشل رو دارم
سلام و درود
از کجا باید تشخیص بدیم کدوم حالت رو استفاده کنیم؟
یعنی چطور باید تشخیص بدیم ضلح رو بنویسیم یا زاویه(کدوم حالت)
با سلام وعرض ادب
دوست عزیز از روی صورت مسله باید ببینید برای تساوی کدام ضلع یا زاویه دلیل داریدبعد ببینید اینهایی که نوشته اید کدام حالت رو به وجود میاره
salam mofid bOd mamnOn
سلام و عرض ادب
ممنون از شما دوست عزیز
ممنون خیلی عالی بود
با سلام
ممنون دوست عزیز
بسیار عالی
با سلام وعرض ادب
ممنون از شما خدا رو شکر که مفید واقع شده
سلام..وقتتون بخیر.عااالی بودتدریستون..خصوصا اینکه فونت درشت رو انتخاب کردین…دعاگوتون هستم وخواهم بود..خیلی از مطالب سایت خوبتون استفاده کردم..سلامت باشید و پویا…
با سلام وعرض ادب
ممنون از نظرات خوب وسازنده ودلگرم کننده شما
خیلی خوب بود از توضیحات تون ممنون ?
با سلام
خرسندیم که مفید بوده
سلام دستتون درد نکنه خیلی مفید بودن و تمامی اشکالات من کل شد
باسلام و ادب
خدا روشکر مفید بوده برای شما
سلام ببخشید حالتهای همنهشتی مستطیل چیا هستند؟
با سلام
برا مستطیل حالت خاص نداریم
میشه یه توضیح مختصر بدید چجوری تشخیص بدیم حالت همنهشتی رو تشخیص بدیم من کلا قاطی میکنم میشه بگید
با سلام
دوست عزیز ببینید اون ضلعها وزاویه هایی که برا مساوی بودنشون دلیل دارید کدوم یک از سه حالت رو پیش میاره فقط از این قسمت زیاد مسئله حل کنید
آیا با حالت دو ضلع و زاویه ی غیر بین می توان گفت دو مثلث با هم هم نهشت اند ؟ اگه نه چرا ؟
خیر چون همچین قضیه وحالتی نداریم
هر شکلی چندتا مشترک داشته باشه همنهشته؟؟؟
با سلام
طبق حالتهای همنهشتی حداقل سه تا از ضلعها وزاویه ها رو براشون باید دلیل تساوی داشته باشیم تا از حالتهای همنهشتی بتونیم استفاده کنیم
اگر توی مسئله از هرکدوم از این حالت ها استفاده کنیم مشکلی نداره
با سلام وادب
نمیشه از هر کدوم دلمون بخواد استفاده کنیم بلکه با توجه به داده های مسئله ببینیم به کدوم میشه استناد کرد
سلام و عرض ادب
ببینید بستگی به دلیل داره. مثلا در مواقعی میتوان هم دو ضلع و زاویه بین و هم میتوان سه ضلع را گفت مثل تمرین ۳ صفحه ۴۸. و در بهضی مواقع نمیتوان دو تا حالت رو گفت مثل تمرین ۴ صفحه ۴۳.
کلا برای همنهشتی ها باید برای هرچه مینویسید یک دلیل قانع کننده نیز باشه تا جواب درست در بیاد.
سلام دوست عزیز
ممنون از پاسخگویی شما
سلام ممنون
فقط یه سوال اینکه چرا حالتهای همنهشتی منحصر در این سه حالی هست مثلا چرا حالت ززز یا ض ض ض و یا حالت ززز ض ض ض نداریم؟
بعد چگونه از داده ها به تناظر زوایا یا اضلاع پی ببریم؟ به عبارت دیگر چه داده هایی دلیل تناظر زوایا و چه داده هایی دلیل تناظر اضلاع هست؟
با سلام وادب
ببینید اولا وقتی دو مثلث برابرند که تمام زاویه وضلع ها برابر باشند یعنی شش جز آنها اما ما همیشه در مسائل اندازه تمام اجزا را نمیدانیم ریاضیدانها اثبات کرده اند که اگر سه ضلع از مثلثی با سه ضلع از مثلث دیگر برابر باشت ند حتما زاویه های آنها نیز باهم برابرند ودو مثلث با هم همنهشت هستند وهمینطور دو زاویه وضلع بین شان نیز اگر از دو مثلث برابر باشند بقیه اجزا نیز برابرند وحالت دو ضلع وزاویه بین که نام اختصاری آنها شده ض ض ض و ض زض و زض ز ولی اگر سه زاویه از مثلثی با سه زاویه از مثلث دیگر برابر باشند لزوما مثلثها برابر نیستند یا دوزاویه برابر باشند ولی ضلع بین شان برابر نباشد نمی توان نتیجه گرفت دومثلث هم نهشت هستند پس فقط سه حالت داریم
باید شما با توجه به داده های مسئله ببینید برای چه ضلع ها وزاویه هایی دلیل برابر بودن دارید ودومثلث به چه حالتی همنهشت هستند بقیه ضلع ها وزاویه هایی که دلیل ندارید میشود اجزا متناظر
با سلام و احترام
عالی بود
با سلام
ممنون از نگاهتون
مرسییی
خواهش میکنم دوست عزيز