ماکزیمم و مینیمم سهمی 〽️📉 – بالا و پایین نمودارتو بشناس!

سلام رفقای ریاضیکا امروز قصد داریم مبحث ماکزیمم و مینیمم سهمی را با هم یادبگیریم. ما در پست رسم سهمی و ویدیو آموزشی آن در مورد رسم نمودار تایع درجه دوم یا همان سهمی صحبت کردیم. در این پست می‌خواهیم در مورد نکات تکمیلی نمودار سهمی مانند ماکزیمم و مینیمم سهمی ، صفرهای تابع درجه دوم، پیدا کردن جواب‌های تقریبی از روی نمودار سهمی، تفسیر نمودار سهمی و نوشتن معادله تابع درجه دوم از روی نمودار آن نکاتی را به شما بیاموزیم.

آموزش ماکزیمم و مینیمم سهمی

همانطور که در پست رسم سهمی به شما آموختیم معادله تابع درجه دوم به فرم گسترده به صورت \(\Large y=a x^2 +bx+c \) می‌باشد که در آن طول راس \(\Large  x_s=-\frac{b}{2a} \)  می‌باشد همانطور که می‌دانید:

• اگر \(\Large a>0 \) دهانه سهمی رو به بالا و تابع در این مواقع در راس یعنی \(\Large  x_s=-\frac{b}{2a} \) دارای کمترین \(\Large  (min) \) مقدار خود می‌باشد.
• اگر \(\Large a<0 \) دهانه سهمی رو به پایین می‌باشد تابع در این مواقع در راس یعنی \(\Large  x_s=-\frac{b}{2a} \) دارای بیشترین \(\Large  (max) \) مقدار خود می‌باشد.

---

---

مثال 1: در تابع \(\Large y=2x^2+4x-1 \) ماکزیمم و مینیمم سهمی را در صورت وجود پیدا کنید.

جواب 1:

\(\LARGE a=2>0  \)

پس دارای مینیمم است.

\(\LARGE x_s=-\frac{4}{2}=-2  \)

\(\LARGE f(-2)  \)

\(\LARGE =2(-2)+4(-2)-1=-1  \)

پس کمترین مقدار این تایع \(\Large -1 \) می‌باشد (مقدار تایع در یک نقطه) همان عرض نقطه می‌باشد.

توجه: ماکزیمم و مینیمم سهمی را می‌توان در مسائل بهینه سازی به راحتی استفاده کرد.

مثال 2: بیشترین مساحت زمینی که می‌توان با یک طناب به طول ۸۸ متر و به شکل مستطیل محصور نمود چند متر مربع است؟

جواب 2:

طول = \(\Large y \) عرض = \(\Large x \)

محیط

\(\LARGE p=2(x+y)  \)

\(\LARGE 2x+2y=88 \rightarrow x+y=44\)

\(\LARGE  y=(44-x) \)

مساحت

\(\LARGE s_{(x)}=xy  \)

\(\LARGE =x(44-x)=44x-x^2  \)

خوب رسیدیم به یک معادله درجه دوم با توجه به اینکه \(\Large a<0 \) است پس ارتفاع این تابع در راس بیشترین مقدار \(\Large  (max) \) را دارد پس:

\(\LARGE x_s=-\frac{b}{2a}=\frac{-44}{-2}=22  \)

پس اگر:

\(\LARGE x=22 , y=22  \)

یعنی اگر این زمین به شکل یک مربع باشد دارای بیشترین مقدار مساحت خواهد بود.

 

\(\LARGE S = 22 \times 22 = 44  \)

توجه: شما در پست بهینه سازی دوازدهم تجربی حل این مسئله و ماکزیمم و مینیمم سهمی را از روش دیگری هم خواهید آموخت.

صفرهای تابع

نقاط برخورد نمودار یک تابع درجه دوم با محور \(\Large x \)ها را صفرهای تابع می‌نامند که در واقع ریشه‌های معادله \(\Large f_{(x)}=0 \) هستند. به عبارت دیگر در این نقاط مقدار تابع \(\Large (y) \) برابر صفر است.

پس داریم:

• الف) می‌دانیم اگر در معادله درجه دوم \(\Large \Delta > 0 \) باشد پس معادله دو ریشه دارد و در این مواقع نمودار محور \(\Large x \)ها را در دو نقطه قطع می‌کند و نمودار آن به یکی از دو شکل زیر خواهد بود.
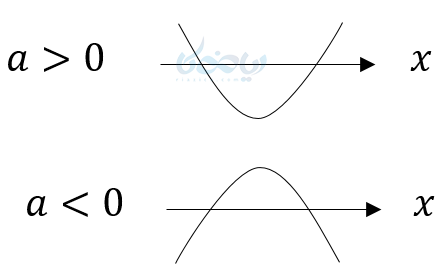  در این مواقع تابع به ازای بعضی مقادیر مثبت و به ازای بعضی از مقادیر منفی می‌باشد.
• ب) اگر در معادله درجه دوم \(\Large \Delta = 0 \) باشد پس معادله یک ریشه دارد و در این مواقع نمودار به محور \(\Large x \)ها مماس خواهد شد و نمودار آن به یکی از دو شکل زیر خواهد بود.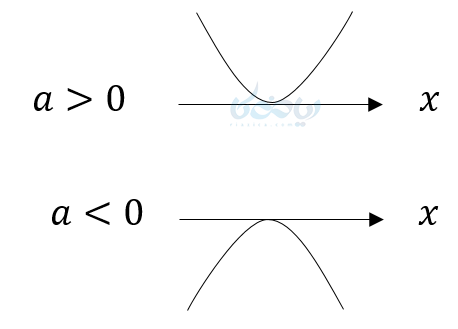در این مواقع تابع به غیر از ریشه به ازای بقیه مقادیر کاملا مثبت یا کاملا منفی می‌باشد.
• ج) اگر در معادله درجه دوم \(\Large \Delta < 0 \) باشد پس معادله ریشه نخواهد داشت و اصلا نمودار محور \(\Large x \)ها را قطع نمی‌کند و نمودار آن به یکی از دو شکل زیر خواهد بود.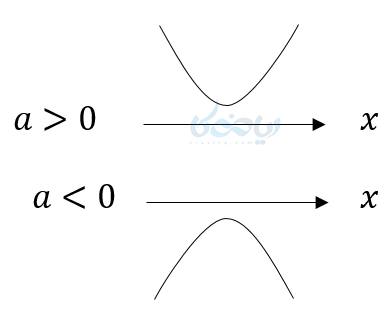در این مواقع تابع به ازای جمیع مقادیر کاملا مثبت یا کاملا منفی می‌باشد.

مثال 3: با توجه به شکل زیر علامت، ریشه‌های تابع و علامت مقدار تابع را مشخص کنید؟

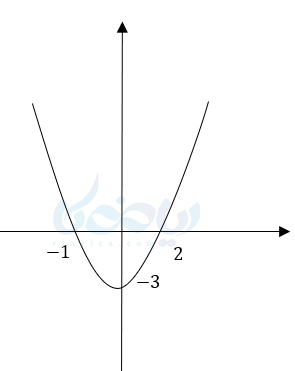
جواب 3:

این تابع دو ریشه دارد یکی منفی و یکی مثبت. \(\Large x=-1,x=2 \) \(\Large a>0 \) می‌باشد و مقدار تابع یا همان \(\Large y \) در بازه \(\Large (2 , +\infty),(-\infty , -1) \) مثبت و در بازه  \(\Large (-1,2) \) منفی می‌باشد.

مثال 4: با توجه به شکل زیر علامت، ریشه‌های تابع و علامت مقدار تابع را مشخص کنید؟

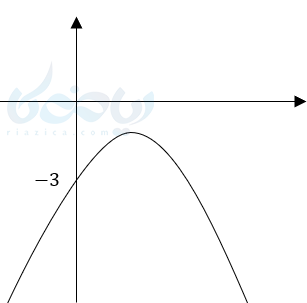
جواب 4:

این تابع ریشه ندارد و به ازای جمع مقادیر تابع منفی است.

---

---

پیدا کردن علامت \(\Large a,b,c \) در معادله درجه دو

نکته مهم: محل تلاقی نمودار با محور عرض‌ها یا همان \(\Large f_{(0)} \) عدد ثابت \(\Large c \) در معادله \(\Large y=ax^2+bx+c \) می‌باشد که به آن عرض از مبدا هم می‌گویند.

در مثال‌های بالا در نمودار الف \(\Large c=-2 \) و در نمودار ب \(\Large c=-3 \) می‌باشد.

از روی نمودار به اطلاعات دیگری هم می‌توان دست پیدا کرد، مانند علامت \(\Large a,b,c \). علامت \(\Large a \) که همه می‌دانیم دهانه رو به بالا \(\Large a>0 \) و دهانه رو به پایین \(\Large a<0 \).

نکته: برای پیدا کردن علامت \(\Large b \) کافیه ببینیم علامت راس با توجه به نمودار چیست و بعد با داشتن علامت \(\Large a \) علامت \(\Large b \) را پیدا می‌کنیم. به مثال زیر دقت کنید.

مثال 5: علامت \(\Large a,b,c \) را در نمودار زیر پیدا کنید، ماکزیمم و مینیمم سهمی را نیز تعیین کنید؟

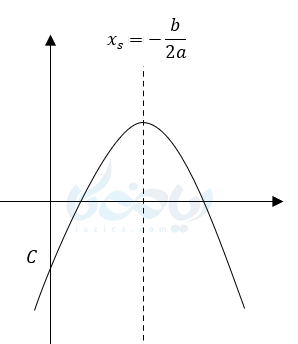
جواب 5:

خوب \(\Large a<0 \) چون دهانه نمودار رو به پایین است. و برای تشخیص ماکزیمم و مینیمم سهمی می‌توان گفت فقط ماکزیمم دارد.

علامت راس مثبت یعنی \(\Large -\frac{b}{2a}>0 \) یک کسر وقتی مثبت می‌شود که صورت و مخرج هم علامت باشند مخرج با توجه به علامت \(\Large a \) منفی است. پس صورت هم باید منفی باشد پس \(\Large b>0 \) است. \(\Large (\frac{-}{-}>0) \) \(\Large c<0 \) چون نمودار محور عرض‌ها را در قسمت پایین قطع کرده است.

نکته: علامت یک کسر به طور کلی به صورت زیر خواهد بود.

\(\LARGE \frac{-}{-}>0  \)

\(\LARGE \frac{+}{+}>0  \)

\(\LARGE \frac{+}{-}<0  \)

\(\LARGE \frac{-}{+}<0  \)

مثال 6: نمودار یک سهمی به صورت زیر است علامت \(\Large a,b,c \)، تعداد ریشه‌ها و علامت ریشه‌ها در صورت وجود پیدا کنید.

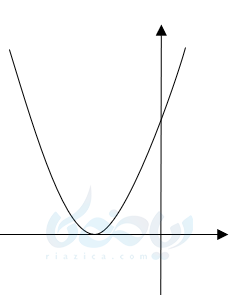
جواب 6:

\(\Large a>0 \) چون دهانه سهمی رو به بالا است.

\(\Large c>0 \) چون در قسمت بالایها محور \(\Large y \)ها را قطع نموده‌ است.

\(\LARGE a>0 \rightarrow b>0 \)

\(\LARGE x_s=-\frac{b}{2a}<0 \)

صورت باید منفی باش تا کسر مثبت شود پس \(\Large b \) باید مثبت شود.

نمودار یک ریشه دارد چون نمودار بر محور \(\Large x \)ها مماس شده و آن یک ریشه هم منفی می‌باشد.

نوشتن معادله تابع درجه دوم از روی نمودار آن

می توان از روی  نمودار یک تابع درجه دوم  معادله مربوط به آن را باتوجه به ریشه ها و راس و محل برخورد آن با محور عرضها بدست آورد کافیست با اطلاعات موجود در شکل \(\Large a,b,c \) را بدست اوریم .

مثال 7: معادله سهمی زیر را با توجه به نمودار آن را بنویسید.

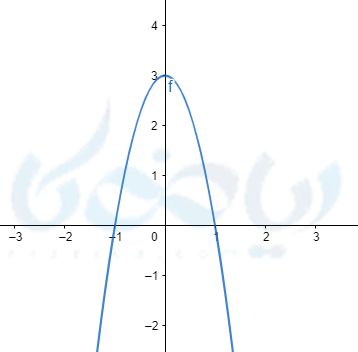
جواب 7:

با توجه به نمودار محور تقارن خط \(\Large x=0 \) است. پس ریشه‌ دیگر این معادله \(\Large x=1 \) می‌باشد.

مقدار \(\Large c \) نیز \(\Large c=3 \) می‌باشد. پس داریم:

\(\LARGE y=ax^2+bx+c \)

\(\LARGE c=3 \)

\(\LARGE (1,0) \rightarrow a+b+3=0 \)

\(\LARGE (-1,0) \rightarrow a-b+3=0 \)

\(\LARGE 2a=-6 \rightarrow a=-3  \)

\(\LARGE b=0  \)

\(\LARGE y=-3x^2+3  \)

نکته: هرگاه ریشه‌ها قرینه یکدیگر باشند \(\Large b=0 \) می‌باشد.

مثال 8: معادله سهمی زیر را بنویسید.

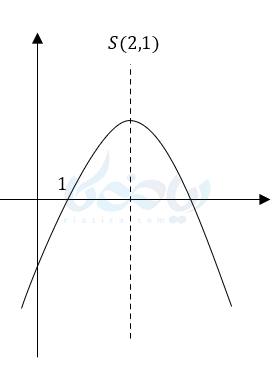
جواب 8:

\(\LARGE y=ax^2+bx+c \)

\(\LARGE (1,0) \rightarrow a+b+c=0 \rightarrow (1)  \)

\(\LARGE (2,1) \rightarrow 4a+2b+c=1 \rightarrow (2) \)

از طرفی \(\Large s \) راس می‌باشد. پس داریم:

\(\LARGE S(2,1) \rightarrow -\frac{b}{2a}=2  \)

\(\LARGE  \rightarrow -b=4a \rightarrow b=-4a \rightarrow (3) \)

رابطه ۳ را در رابطه ۱ و ۲ جایگذای می‌کنیم و خواهیم داشت:

\(\LARGE -3a+c=0  \)

\(\LARGE -4a+c=1 \)

\(\LARGE a=-1 , c=-3 , b=4 \)

پس معادله سهمی می‌شود:

\(\LARGE y=-x^2+4x-3 \)

قبل از خواندن این پست حتما پست روابط بین ریشه های معادله درجه دوم را بخوانید ودر ادامه پست حل معادلات گویا را مطالعه کنید.

ویدیو ماکزیمم ومینیمم سهمی

در این ویدیو با استفاده از برنامه جئوجبرا تغییرات پارامترهای تابع درجه دوم وماکزیمم ومینیمم سهمی آموزش داده شده است.

زنگ آخر ماکزیمم و مینیمم سهمی

خوب دوستان با هم ماکزیمم و مینیمم سهمی و طرز نوشتن معادله رو از روی سهمی را یادگرفتیم. با چندتا مثال و خوندن و مرور این پست به راحتی می‌تونید روی این بحث مسلط شوید.

رفقای ریاضیکا هر سوالی از این درس و ریاضی یازدهم تجربی داشتید در قسمت دیدگاه‌ها برایمان بنویسید. کارشناسای ریاضیکا قطعا به شما عزیزان پاسخ می‌دهند.

---

---