آموزش ریاضی پایه دوازدهم تجربی
معادلات مثلثاتی ریاضی دوازدهم ✏️📝 – یادگیری از طریق حل مثال
در این درسنامه قصد داریم تا به معادلات مثلثاتی ریاضی دوازدهم و روش حل آنها بپردازیم. ابتدا نسبت های مثلثاتی زوایای دو برابر کمان را بررسی میکنیم. سپس، معادلات مثلثاتی را به دو دستهء کلی معادلات سینوسی و کسینوسی تقسیم کرده و در مورد هریک بحث میکنیم. همان طور که خواهیم دید، با استفاده از دایره مثلثاتی میتوانیم جوابهای کلی معادلات سینوسی و کسینوسی را به دست آوریم.
نسبت های مثلثاتی زوایای دو برابر کمان
با نسبتهای مثلثاتی و روابط بین آنها در سالهای قبل آشنا شدهاید. منظور از نسبت های مثلثاتی زوایای دو برابر کمان، ارتباط سینوس، کسینوس، تانژانت و کتانژانت یک زاویه با دو برابر آن است. یعنی مثلا می خواهیم ببینیم \(\Large \sin(2 \alpha) \) چه ارتباطی با \(\Large \sin( \alpha)\) دارد. یا \(\Large \cos(2 \alpha) \) چه ارتباطی با \(\Large \cos( \alpha) \) دارد؟ چهار رابطۀ مهم در مورد این نسبتها داریم که یکی مربوط به سینوس و سه تای دیگر آن مربوط به کسینوس است. این روابط عبارتند از:
- \(\LARGE \sin 2 \alpha=2 \sin\alpha \cos\alpha \)
- \(\LARGE \cos 2 \alpha=\cos^2 \alpha-\sin^2 \alpha\)
- \(\LARGE \cos 2 \alpha=1-2\sin^2(\alpha) \)
- \(\LARGE \cos 2 \alpha=2\cos^2(\alpha)-1 \)
اثبات هندسی روابط دو برابر کمان توسط ابوالوفا بوزجانی ارائه شده است. با اینکه این اثبات جزء ارزشیابی نیست، اما اگر علاقه دارید حتما این قسمت را در کتاب درسی مطالعه کرده و لذت ببرید! از نسبت های مثلثاتی زوایای دو برابر کمان در حل معادلات مثلثاتی ریاضی دوازدهم بسیار استفاده خواهیمکرد.
مثال 1: \(\Large \sin 45^{\circ}\) و \(\Large \cos 45^{\circ}\) را به دست آورید.
حل:
\(\LARGE \cos 90^{\circ}=1-2 \sin^2 45^{\circ} \)
\(\LARGE 0=1-2 \sin^2 45^{\circ}\)
\(\LARGE \sin^2 45^{\circ}=\frac{1}{2}\)
\(\LARGE \sin 45^{\circ}=\pm \sqrt{\frac{1}{2}}=\pm \frac{\sqrt{2}}{2}\)
از آنجاییکه \(\Large 45^{\circ}\) در ربع اول است، پاسخ مثبت قابل قبول است. در نتیجه \(\Large \sin 45^{\circ}=\frac{\sqrt{2}}{2}\). برای محاسبۀ \(\Large \cos 45^{\circ}\)، هم میتوانیم از رابطۀ \(\Large \cos\alpha=\sqrt{1-\sin^2\alpha}\) استفاده کنیم و هم میتوانیم از نسبتهایی که در بالا گفتیم استفاده کنیم. برای اینکه محاسبۀ زاویه با استفاده از روابط دو برابر کمان را بیشتر تمرین کرده باشیم،\(\Large \cos 45^{\circ}\) را با استفاده از روابط بالا به دست میآوریم:
\(\LARGE \sin 90^{\circ}=2\sin 45^{\circ}\cos 45^{\circ} \)
\(\LARGE 1=2\times \frac{\sqrt{2}}{2} \cos 45^{\circ} \)
\(\LARGE \cos 45^{\circ}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2} \)
معادلات مثلثاتی ریاضی دوازدهم
تعریف معادله مثلثاتی:معادلاتی که بر حسب نسبتهای مثلثاتی یک زاویه مجهول نوشته می شوند را معادله مثلثاتی می نامند.
جواب معادله مثلثاتی :مقدارهایی که به ازای انها معادله مثلثاتی برقرار شود را جواب معادله می نامند.
در معادلات مثلثاتی معمولا با عباراتی رو به رو هستیم که شامل سینوس، کسینوس، تانژانت، کتانژانت و یا ترکیبی از آنها هستند. با توجه به رابطهای که بین این نسبتها وجود دارد میتوانیم معادلات مثلثاتی ریاضی دوازدهم را به فرم یک معادلۀ سینوسی یا کسینوسی تبدیل کنیم. حل هر کدام از این فرمها را در مختصات دکارتی بررسی میکنیم. سپس با استفاده از دایره مثلثاتی جوابهای کلی هر یک را به دست میآوریم.
معادلات سینوسی
ابتدا معادلاتی به فرم \(\Large \sin x=c\) را بررسی میکنیم. با حل چند مثال از این معادلات، جوابهای کلی معادلات به فرم \(\Large \sin x=c\) را در معادلات مثلثاتی ریاضی دوازدهم به دست خواهیم آورد.
مثال 2: جوابهای معادلۀ \(\Large \sin x=0\) را به دست آورید.
حل: به نمودارتابع \(\Large f(x)=\sin x\) در شکل زیر نگاه کنید.
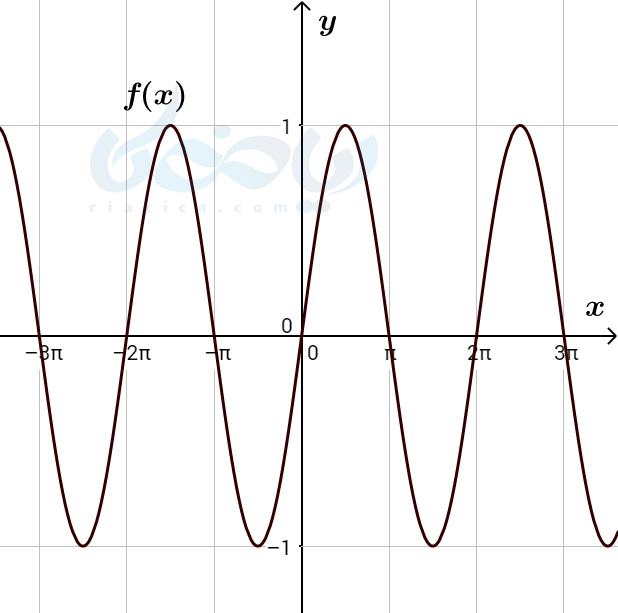
جوابهای معادلۀ \(\Large \sin x=0\) برابر است با نقاط برخورد تابع \(\Large f(x)=\sin x\) با خط \(\Large y=0\) که همان محور \(\Large x\) هاست. بنابراین جواب معادله برابر است با
\(\Large x=\dots,-2\pi,-\pi,0,\pi,2\pi,\dots\)
جواب معادله را می توان به صورت \(\Large x=k\pi\) که \(\Large k\) یک عدد صحیح است نیز نشان داد. این مثال و مثال بعد، دو حالت خاص از معادلات مثلثاتی ریاضی دوازدهم هستند.
مثال 3: جوابهای معادلۀ \(\Large \sin x=1\) را به دست آورید.
حل: به نمودارتابع \(\Large f(x)=\sin x\) و خط \(\Large y=1\) در شکل زیر نگاه کنید.
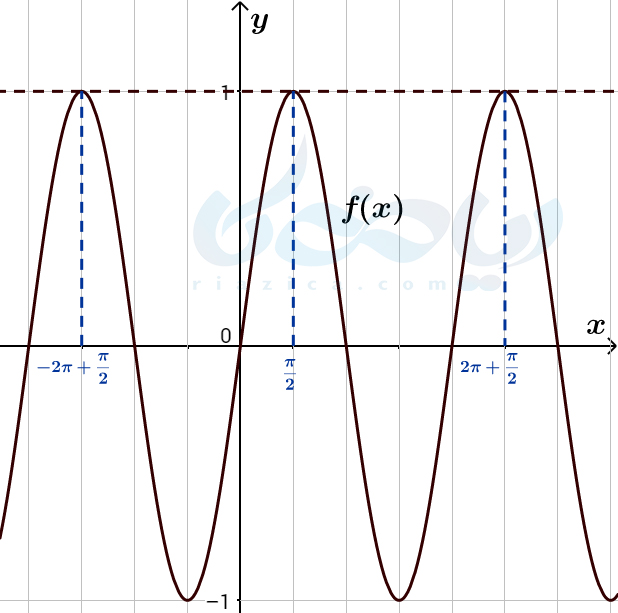
جوابهای معادلۀ \(\Large \sin x=1\) برابر است با نقاط برخورد تابع \(\Large f(x)=\sin x\) با خط \(\Large y=1\). بنابراین جواب معادله برابر است با
\(\Large x=\dots,-2\pi+\frac{\pi}{2},\frac{\pi}{2},2\pi+\frac{\pi}{2},\dots\)
جواب معادله را می توان به صورت \(\Large x=2k\pi+\frac{\pi}{2}\) که \(\Large k\) یک عدد صحیح است نیز نشان داد. در مثال بعدی، معادلهای متفاوت تر از این مثال و مثال قبلی از معادلات مثلثاتی ریاضی دوازدهم خواهیم دید.
مثال 4: جوابهای معادلۀ \(\Large \sin x=\frac{\sqrt{3}}{2}\) را به دست آورید.
حل: به نمودارتابع \(\Large f(x)=\sin x\) و خط \(\Large y=\frac{\sqrt{3}}{2}\) در شکل زیر نگاه کنید.
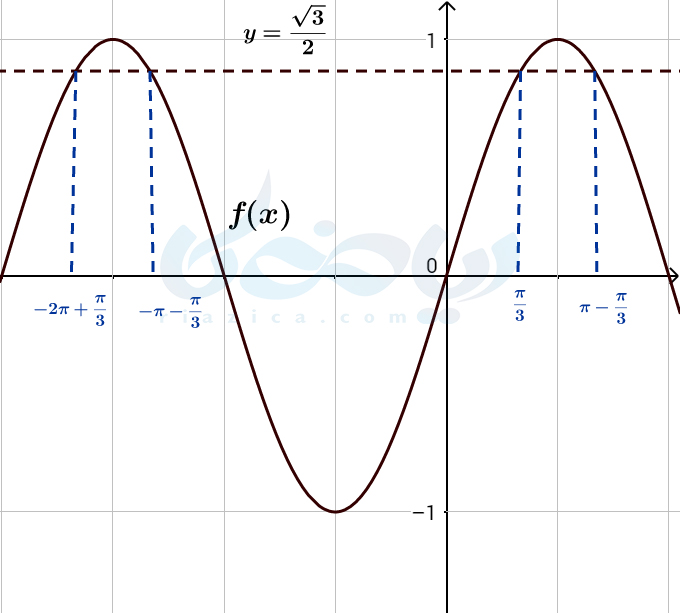
جوابهای معادلۀ \(\Large \sin x=\frac{\sqrt{3}}{2}\) برابر است با نقاط برخورد تابع \(\Large f(x)=\sin x\) با خط \(\Large y=\frac{\sqrt{3}}{2}\). بنابراین جواب معادله برابر است با
\(\Large x=\dots,-\pi-\frac{\pi}{3},\frac{\pi}{3},\pi-\frac{\pi}{3},\dots\)
جواب معادله را می توان به صورت \(\Large x=2k\pi+\frac{\pi}{3}\) و \(\Large x=(2k+1)\pi-\frac{\pi}{3}\) که \(\Large k\) یک عدد صحیح است نیز نشان داد.
استفاده از دایره مثلثاتی برای معادلات سینوسی
در مثالهای 2 تا 4 میتوانستیم به جای استفاده از مختصات دکارتی از دایره مثلثاتی نیز استفاده کنیم (در صورتی که دایره مثلثاتی را فراموش کردهاید، به دلیل کابرد دایره مثلثاتی در معادلات مثلثاتی ریاضی دوازدهم ، درسنامۀ دایره مثلثاتی یا دایره واحد را مرور کنید). مثال 4 را در نظر بگیرید. میخواهیم جواب معادلۀ \(\Large \sin x=\frac{\sqrt{3}}{2}\) را پیدا کنیم. دایرۀ مثلثاتی و خط \(\Large y=\frac{\sqrt{3}}{2}\) را مطابق شکل زیر رسم میکنیم:
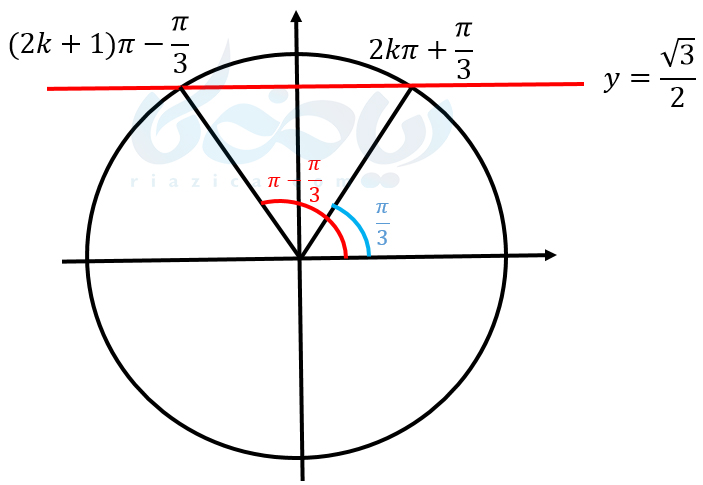
همان طور که میبینید، سینوس زوایایی که هم انتها با زاویۀ \(\Large \frac{\pi}{3}\) هستند، یعنی سینوس زوایای \(\Large 2k\pi+\frac{\pi}{3}\) برابر با \(\Large \frac{\sqrt{3}}{2}\) است. علاوه بر این، سینوس زوایایی که هم انتها با \(\Large \pi-\frac{\pi}{3}\) هستند، یعنی سینوس زوایای \(\Large (2k+1)\pi-\frac{\pi}{3}\) نیز برابر با \(\Large \frac{\sqrt{3}}{2}\) است.
جوابهای کلی معادلات سینوسی
فرض کنید میخواهیم معادلهای به شکل \(\Large \sin x=a\) را که \(\Large -1\leq a \leq 1\) است، به عنوان یکی از معادلات مثلثاتی ریاضی دوازدهم حل کنیم. زاویهای مانند \(\Large \alpha\) وجود دارد که سینوس آن برابر با \(\Large a\) باشد. بنابراین میتوانیم معادلهی \(\Large \sin x=a\) را به صورت \(\Large \sin x=\sin\alpha\) بازنویسی کنیم. اما چه زوایایی هستند که سینوسی برابر با سینوس زاویۀ \(\Large \alpha\) دارند. در شکل زیر دایره مثلثاتی و زاویۀ \(\Large \alpha\) را رسم کردهایم.
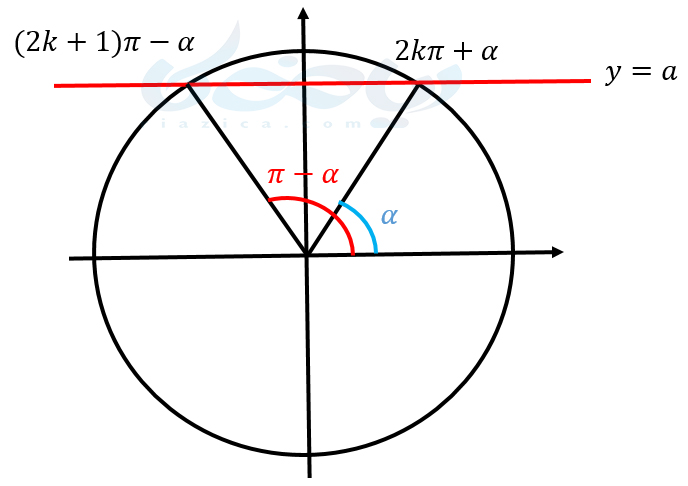
کاملا مشخص است که زوایایی به شکل \(\Large 2k\pi+\alpha\) و \(\Large (2k+1)\pi-\alpha\)، سینوسی برابر با سینوس زاویۀ \(\Large \alpha\) دارند. بنابراین جوابهای کلی معادلۀ \(\Large \sin x=\sin \alpha\) به دو شکل کلی \(\Large 2k\pi+\alpha\) و \(\Large (2k+1)\pi-\alpha\) است (\(\Large k\) یک عدد صحیح است).
پس به طور کلی داریم:
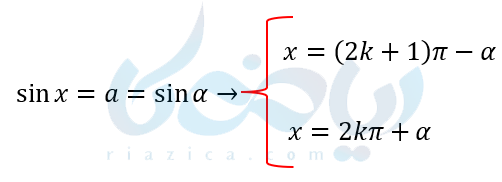
مثال از معادلات سینوسی
مثال 5: معادلۀ \(\Large \sin 4x=\frac{1}{2}\) را حل کنید.
حل:
\(\Large\sin 4x=\frac{1}{2}=\sin \frac{\pi}{6}\)
\(\Large 4x=2k\pi+\frac{\pi}{6}, (2k+1)\pi-\frac{\pi}{6}\)
\(\Large x=k\frac{\pi}{2}+\frac{\pi}{24}, (2k+1)\frac{\pi}{4}-\frac{\pi}{24}\)
مثال 6: معادلۀ \(\Large 4 \sin x+\sqrt{8}=0\) را حل کنید.
حل:
\(\LARGE 4 \sin x+\sqrt{8}=0 \)
\(\LARGE 4 \sin x=-\sqrt{8}\)
\(\LARGE \sin x=-\frac{\sqrt{8}}{4}\)
\(\LARGE \sin x=-\frac{2\sqrt{2}}{4}=-\frac{\sqrt{2}}{2}\)
\(\LARGE \sin x=\sin \frac{5\pi}{4}\)
\(\Large x=2k\pi+5\frac{\pi}{4}, (2k+1)\pi-5\frac{\pi}{4}\)
حالات خاص معادلات مثلثاتی سینوسی در یک نگاه به صورت زیر است.
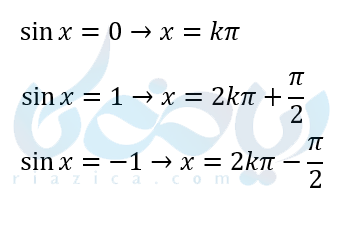
معادلات کسینوسی
دستۀ دیگر از معادلات مثلثاتی ریاضی دوازدهم ، معادلات کسینوسی هستند. برای معادلات کسینوسی نیز تمام مراحلی که برای معادلات سینوسی انجام دادیم، میتوان انجام داد. به مثال زیر دقت کنید.
مثال 7: جوابهای معادلۀ \(\Large \cos x=\frac{1}{2}\) را به دست آورید.
حل: به نمودارتابع \(\Large f(x)=\cos\) و خط \(\Large y=\frac{1}{2}\) در شکل زیر نگاه کنید.
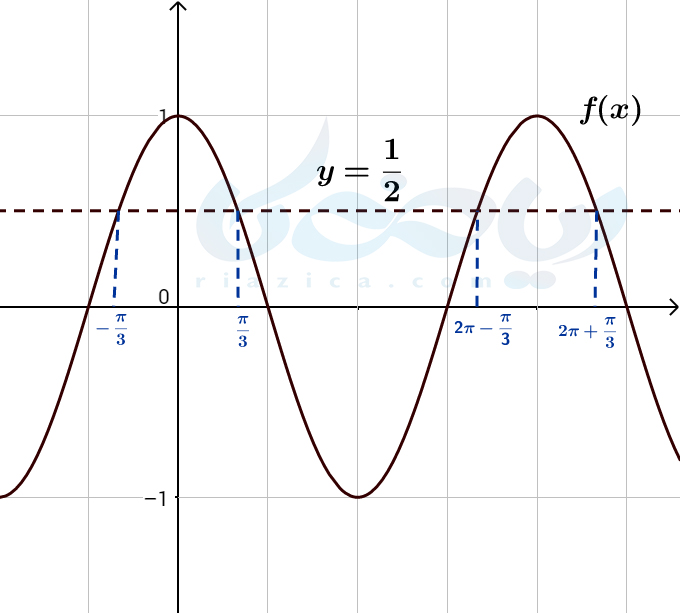
جوابهای معادلۀ \(\Large \cos x=\frac{1}{2}\) برابر است با نقاط برخورد تابع \(\Large f(x)=\cos x\) با خط \(\Large y=\frac{1}{2}\). بنابراین جواب معادله برابر است با
\(\Large x=\dots,-\frac{\pi}{3},\frac{\pi}{3},2\pi-\frac{\pi}{3},2\pi+\frac{\pi}{3},\dots\)
جواب معادله را می توان به صورت \(\Large x=2k\pi\pm\frac{\pi}{3}\) که \(\Large k\) یک عدد صحیح است نیز نشان داد.
استفاده از دایره مثلثاتی برای معادلات کسینوسی
در مثال 7 و به طور کلی در دیگر معادلات مثلثاتی ریاضی دوازدهم میتوانستیم به جای استفاده از مختصات دکارتی از دایره مثلثاتی نیز استفاده کنیم. مثال 7 را در نظر بگیرید. میخواهیم جواب معادلۀ \(\Large \cos x=\frac{1}{2}\) را پیدا کنیم. دایرۀ مثلثاتی و خط \(\Large x=\frac{1}{2}\) را مطابق شکل زیر رسم میکنیم:
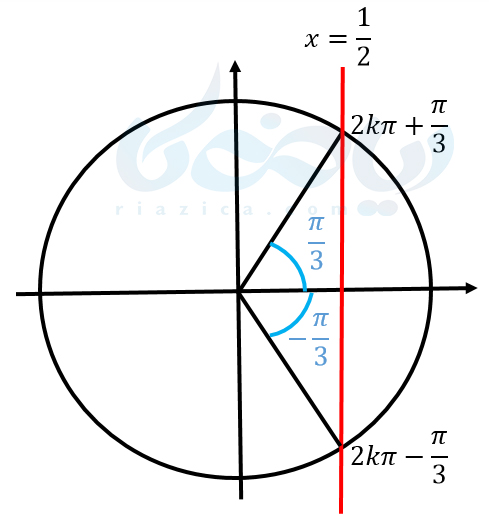
همان طور که میبینید، کسینوس زوایایی که هم انتها با زاویۀ \(\Large \frac{\pi}{3}\) هستند، یعنی کسینوس زوایای \(\Large 2k\pi+\frac{\pi}{3}\) برابر با \(\Large \frac{1}{2}\) است. علاوه بر این، کسینوس زوایایی که هم انتها با \(\Large -\frac{\pi}{3}\) هستند، یعنی کسینوس زوایای \(\Large 2k\pi-\frac{\pi}{3}\) نیز برابر با \(\Large \frac{1}{2}\) است.
جوابهای کلی معادلات کسینوسی
فرض کنید میخواهیم معادلهای به شکل \(\Large \cos x=a\) را که \(\Large -1\leq a \leq 1\) است، به عنوان یکی از معادلات مثلثاتی ریاضی دوازدهم حل کنیم. زاویهای مانند \(\Large \alpha\) وجود دارد که کسینوس آن برابر با \(\Large a\) باشد. بنابراین میتوانیم معادلهی \(\Large \cos x=a\) را به صورت \(\Large \cos x=\cos\alpha\) بازنویسی کنیم. اما چه زوایایی هستند که کسینوسی برابر با کسینوس زاویۀ \(\Large \alpha\) دارند. در شکل زیر دایره مثلثاتی و زاویۀ \(\Large \alpha\) را رسم کردهایم.
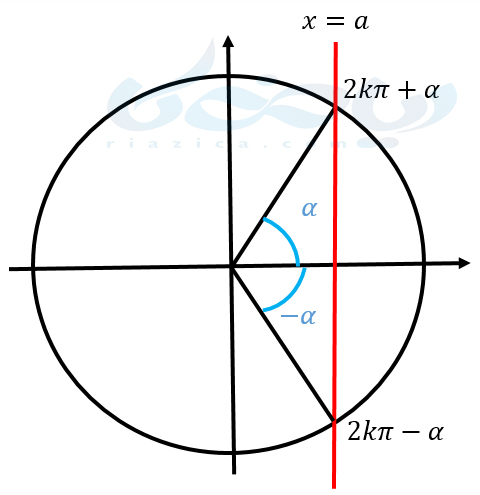
کاملا مشخص است که زوایایی به شکل \(\Large 2k\pi+\alpha\) و \(\Large 2k\pi-\alpha\)، کسینوسی برابر با کسینوس زاویۀ \(\Large \alpha\) دارند. بنابراین جوابهای کلی معادلۀ \(\Large \cos x=\cos\alpha\) به دو شکل کلی \(\Large 2k\pi+\alpha\) و \(\Large 2k\pi-\alpha\) است (\(\Large k\) یک عدد صحیح است).
پس به طور کلی در معادلات مثلثاتی کسینوسی داریم:
![]()
مثال از معادلات کسینوسی
مثال 8: معادلۀ \(\Large \cos 3x=\frac{\sqrt{3}}{2}\) را حل کنید.
حل:
\(\LARGE \cos 3x=\frac{\sqrt{3}}{2}=\cos \frac{\pi}{6}\)
\(\LARGE 3x=2k\pi\pm\frac{\pi}{6}\)
\(\LARGE x=2k\frac{\pi}{3}\pm\frac{\pi}{18}\)
مثال 9: معادلۀ \(\Large 4 \cos x-\sqrt{8}=0\) را حل کنید.
حل:
\(\LARGE 4 \cos x-\sqrt{8}=0 \)
\(\LARGE \cos x=\frac{\sqrt{8}}{4}\)
\(\LARGE \cos x=\frac{2\sqrt{2}}{4}=\frac{\sqrt{2}}{2}\)
\(\LARGE \cos x=\cos \frac{\pi}{4}\)
\( \LARGE x=2k\pi \pm \frac{\pi}{4} \)
حالات خاص معادلات مثلثاتی کسینوسی در یک نگاه به صورت زیر است:
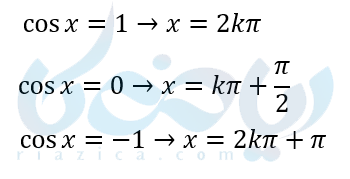
مثال از معادلات مثلثاتی ریاضی دوازدهم
مثال 10: معادلۀ \(\Large \cos 2x -\cos x +1=0\) را حل کنید.
حل:
\(\LARGE \cos 2x-\cos x+1=0\)
\(\Large (2\cos^2x-1)-\cos x+1=0\)
\(\LARGE 2\cos^2x-\cos x=0\)
\(\LARGE \cos x(2\cos x-1)=0\)
\(\Large \cos x=0 \Rightarrow \cos x=\cos \frac{\pi}{2}\)
\(\LARGE \Rightarrow x=2k\pi\pm\frac{\pi}{2}\)
\(\Large \cos x=\frac{1}{2} \Rightarrow \cos x=\cos \frac{\pi}{3}\)
\(\LARGE \Rightarrow x=2k\pi\pm\frac{\pi}{3}\)
مثال 11: معادلۀ \(\Large \sin x \cos x=\frac{1}{4}\) را حل کنید.
حل:
\(\LARGE \sin x \cos x=\frac{1}{4}\)
\(\LARGE \frac{1}{2}\times2\sin x \cos x=\frac{1}{4}\)
\(\LARGE \frac{1}{2}\times\sin 2x =\frac{1}{4}\)
\(\LARGE \sin 2x =\frac{1}{2}\)
\(\LARGE \sin 2x =\sin \frac{\pi}{6}\)
\(\Large 2x=2k\pi+\frac{\pi}{6}, (2k+1)\pi-\frac{\pi}{6}\)
\(\Large x=k\pi+\frac{\pi}{12}, (2k+1)\frac{\pi}{2}-\frac{\pi}{12}\)
مثال 12: معادلۀ \(\Large \sin x -\cos 2x =0\) را حل کنید.
حل:
\(\LARGE \sin x – \cos 2x=0\)
\(\LARGE \sin x – (1-2\sin^2x)=0\)
\(\LARGE 2\sin^2x+\sin x-1=0\)
حال میتوانیم با تغییر متغیر \(\Large \sin x=t\) به یک معادلۀ درجه دوم برسیم (در صورتی که روش حل معادلات درجه دوم را فراموش کردهاید، قبل از خواندن ادامۀ حل، درسنامۀ آموزش حل معادله درجه دو را مرور کنید). از این نوع تغییر متغیرها در معادلات مثلثاتی ریاضی دوازدهم بسیار استفاده خواهیم کرد. با این تغییر متغیر خواهیم داشت:
\(\LARGE 2t^2+t-1=0\)
\(\LARGE t=\frac{-1\pm\sqrt{1+8}}{4}\)
\(\LARGE t=-1,\frac{1}{2}\)
\(\LARGE \sin x=-1,\frac{1}{2}\)
برای \(\Large \sin x=-1\) پاسخ به صورت زیر خواهد بود:
\(\LARGE x=2k\pi-\frac{\pi}{2}\)
برای \(\Large \sin x=\frac{1}{2}\) پاسخ به صورت زیر خواهد بود:
\(\Large x=2k\pi+\frac{\pi}{6} , (2k+1)\pi-\frac{\pi}{6} \)
نکته: در معادله \(\Large \sin x = a , cos x = a\) فقط در صورتیکه \(\Large -1 \leq a \leq 1 \) باشد معادله جواب دارد در غیر اینصورت معادله جواب ندارد.
زنگ آخر کلاس معادلات مثلثاتی ریاضی دوازدهم
در درسنامهای که مربوط به پایه ریاضی دوازدهم تجربی بود با هم خواندیم، ابتدا نسبت های مثلثاتی زوایای دو برابر کمان را بررسی کردیم. سپس، به معادلات مثلثاتی پرداختیم. معادلات مثلثاتی ریاضی دوازدهم را به دو دستۀ کلی سینوسی و کسینوسی تقسیم کرده و جوابهای کلی هر یک را به دست آوردیم. همان طور که در مثالهای انتهای درسنامه دیدیم، از نسبتهای مثلثاتی زوایای دو برابر کمان در حل معادلات مثلثاتی بسیار زیاد استفاده میشود.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث معادلات مثلثاتی ریاضی دوازدهم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





سلام. عالی بود. فقط معادله 4cosx−√8=0
احتمالا پاسخ اشتباه تایپی داره. (فکر کنم پاسخ 2kپی به اضافه منهای پی چهارم باشد).
سلام و عرض ادب
ممنون از توجهی که داشتید. اصلاح شد.
موفق باشید.
سلام روزتون بخیر
ببخشید 2k یعنی چی ؟kچه عددی رو نشون میده؟
با سلام
Kهر عدد صحیح میتونه باشه و2k عددهای زوج رو نشون میده
تو دایره مختسات نشون دهنه جایگاه شروع هستش با همون درجه 0و180
عالی بود
سلام میشه لطفا روش حل
sin6x+sin4x=0
بهم بگید؟!
sin(5x+x)+sin(5x-x)=sin5xcosx+cos5xsinx+sin5xcosx-cos5xsinx=2sin5xcosx=0sin5x=0
5x=kp > x=kp/5
cosx=0 > x=kp+p/2
سلام توی حل معادلات مثلثاتی میتونیم دوطرف تسلوی رو بر یک نسبت مثلثاتی ساده کنیم؟؟
با سلام بله به شرطی که کمان اون نسبت مثلثاتی مجهول نباشه
سلام ممکنه مثال ۱۱ رو توضیح بدید ممنون میشم
سلام دوست عزیز
ابتدا دو طرف رو در یک دوم ضرب کردیم تا بتونیم از رابطه دو برابر کمان استفاده کنیم وبقیه معادله رو هم که بالاتر توضیح دادیم