آموزش ریاضی پایه نهم
شکل های متشابه ریاضی نهم ◼️🔁 – شرط‌هاشو ببین!
دی
در درسنامۀ شکل های متشابه ریاضی نهم ابتدا تشابه را تعریف می‌کنیم. سپس برای درک بهتر، در مثال‌های مختلف، شکل‌های متشابه را مورد بررسی قرار می‌دهیم. در انتها نیز نسبت تشابه را تعریف کرده و مقدار آن را برای شکل‌های مختلف به دست می‌آوریم. با مطالعۀ این درسنامه و حل مثال‌های آن، مشکلی در درک مبحث تشابه نخواهید داشت. با ما تا انتها همراه باشید.
تعریف تشابه
دو چند ضلعی با یکدیگر متشابه‌اند هر گاه دو شرط زیر برقرار باشند:
- اندازۀ زوایای دو شکل، نظیر به نظیر برابر باشد.
- اضلاع متناظر دارای یک نسبت باشند.
منظور از شرط دوم چیست؟ برای اینکه بهتر متوجه شوید، مثال زیر از درسنامۀ شکل های متشابه ریاضی نهم را در نظر بگیرید.
مثال از مثلث‌های متشابه
مثال 1: مثلث‌های \(\Large ABC\) و \(\Large A’B’C’\) را در شکل زیر در نظر بگیرید.
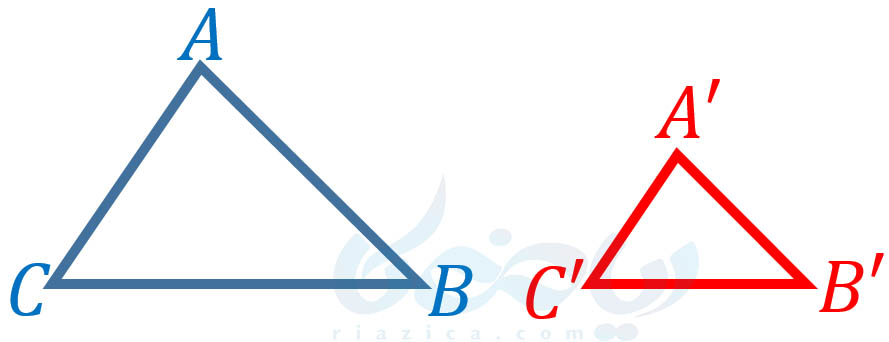
اگر رابطۀ زیر بین اضلاع دو مثلث برقرار باشد، می‌گوییم نسبت اضلاع متناظر با یکدیگر برابر است:
\(\LARGE \frac{AB}{A’B’}=\frac{BC}{B’C’}=\frac{CA}{C’A’}\)
در واقع رابطۀ بالا به معنی برقرار شرط دوم تشابه است که در ابتدای درسنامۀ شکل های متشابه ریاضی نهم گفتیم. به عبارت دیگر می‌توان گفت، اگر اضلاع \(\Large ABC\) را به یک نسبت بزرگ یا کوچک کنیم یا تغییری ندهیم، مثلث \(\Large A’B’C’\) به دست می‌آید. اگر در این دو مثلث، اندازۀ زوایای متناظر نیز با یکدیگر برابر باشد، یعنی داشته باشیم:
\(\LARGE \hat{A}=\hat{A’}\)
\(\LARGE \hat{B}=\hat{B’}\)
\(\LARGE \hat{C}=\hat{C’}\)
در این صورت می‌گوییم دو مثلث متشابه‌اند. به مثال‌های بعدی از درسنامۀ شکل های متشابه ریاضی نهم توجه کنید.
مثال از مربع‌های متشابه در شکل های متشابه ریاضی نهم
مثال 2: ثابت کنید مربع‌های \(\Large ABCD\) و \(\Large A’B’C’D’\) در شکل زیر متشابه‌اند.
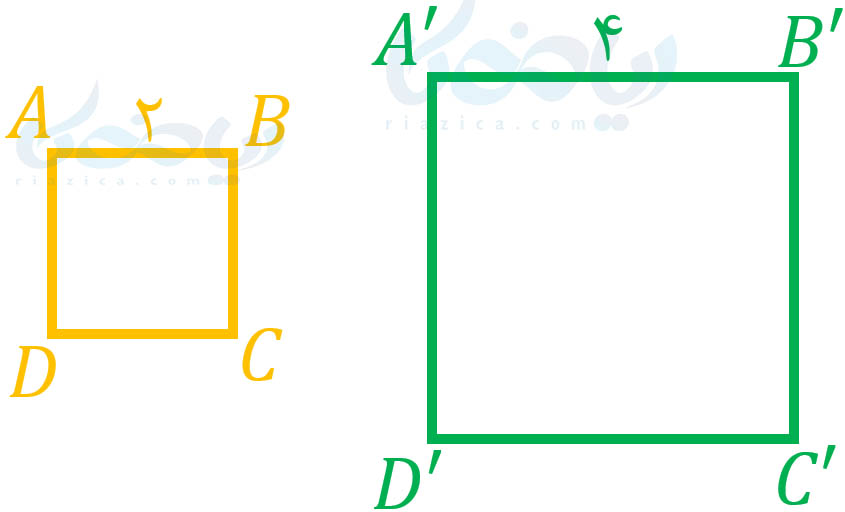
حل: تمام زوایا در هر دو شکل برابر است با \(\Large 90\) درجه. بنابراین شرط اول تشابه برقرار است. فقط باید شرط دوم را چک کنیم. نسبت اضلاع برابر است با:
\(\LARGE \frac{AB}{A’B’}=\frac{2}{4}\)
از آنجاییکه اضلاع یک مربع با یکدیگر برابرند، نسبت اضلاع دیگر نیز برابر با \(\Large \frac{2}{4}\) است. یعنی داریم:
\(\LARGE \frac{BC}{B’C’}=\frac{CD}{C’D’}=\frac{DA}{D’A’}=\frac{2}{4}\)
بنابراین شرط دوم تشابه نیز برقرار است و دو مربع متشابه هستند. از این مثال از درسنامۀ شکل های متشابه ریاضی نهم می‌توان یک نتیجۀ مهم گرفت. هر دو مربعی با یکدیگر متشابه‌اند. زیرا فرض کنید در همین مثال به جای \(\Large 2\) و \(\Large 4\) اعداد دیگری داشتیم. در این صورت زوایا که باز هم برابر با \(\Large 90\) درجه و با هم برابر بود. اضلاع مربع هم چون با هم برابر هستند، نسبت اضلاع با یکدیگر برابر بود. بنابراین باز هم دو شکل با یکدیگر متشابه می‌شدند. پس هر دو مربعی با یکدیگر متشابه‌اند.
چه شکل‌هایی همیشه با یکدیگر متشابه‌اند؟
سوال بالا خیلی دقیق نیست اما شاید منظورمان را خوب برساند. در مثال قبل ثابت کردیم هر دو مربعی با یکدیگر متشابه‌اند. آیا اشکال دیگری مانند مربع پیدا می‌شوند که این شرایط را داشته باشند؟ منظور این سوال همین است. مثلاً هر دو مثلث متساوی‌الاضلاع نیز با یکدیگر متشابه‌اند. زیرا زوایای آن‌ها که در هر حالت برابر با \(\Large 60\) درجه بوده و با یکدیگر مساوی است. اضلاع هر مثلث متساوی‌الاضلاع نیز با یکدیگر برابر است. بنابراین هر نسبتی که یک ضلع از یکی، با ضلعی از دیگری داشته باشد، بقیۀ اضلاع آن مثلث نیز با اضلاع مثلث دیگر دارند. درست مانند مربع. به طور کلی هر شکلی که دارای زوایای برابر و اضلاع برابر باشد، با اشکال دیگر از آن دسته متشابه است. به عبارت دیگر، تمام \(\Large n\)-ضلعی‌های منتظم با \(\Large n\) یکسان، با یکدیگر متشابه اند. مثلاً تمام \(\Large 5\) ضلعی‌های منتظم با یکدیگر متشابه‌اند. به مثال‌های بعدی از درسنامۀ شکل های متشابه ریاضی نهم دقت کنید.
تشابه دو مثلث متساوی الساقین
مثال 3: همان‌طور که گفتیم، تمام \(\Large n\)-ضلعی‌های منتظم با \(\Large n\) یکسان با یکدیگر متشابه‌اند. آیا تمام مثلث‌های متساوی‌الساقین نیز با یکدیگر متشابه‌اند؟
حل: با مثال نقض نشان می‌دهیم که لزوماً هر دو مثلث متساوی الساقین با یکدیگر متشابه نیستند (در صورتی که استفاده از مثال نقض در استدلال را فراموش کرده‌اید، درسنامۀ استدلال ریاضی نهم را مرور کنید). دو مثلث متساوی الساقین زیر را در نظر بگیرید:
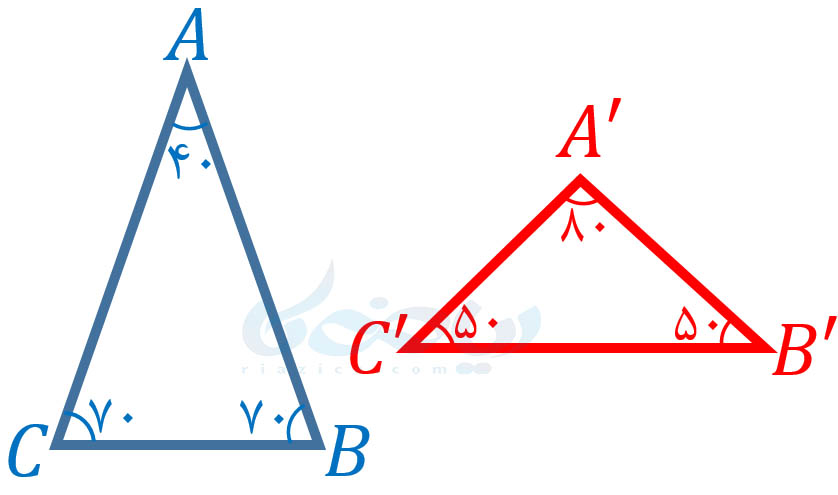
حتی اصلاً مهم نیست بدانیم اندازۀ اضلاع چه قدر است. همین که هیج زاویه‌ای از مثلث \(\Large ABC\) با هیچ زاویه‌ای از مثلث \(\Large A’B’C’\) برابر نیست، نشان می‌دهد که این دو مثلث متشابه نیستند. بنابراین این دو مثلث مثال نقضی هستند برای حکم “هر دو مثلث متساوی‌الساقین متشابه‌اند”.
برای علاقه‌مندان: برای اثبات دقیق‌تر باید نشان دهیم که مثلث‌های متساوی‌الساقین با چنین زوایایی وجود دارند. به علت ساده بودن اثبات این موضوع و برای طولانی نشدن درسنامه، آن را به خواننده واگذار می‌کنیم (اگر نتوانستید اثبات کنید، در دیدگاه‌ها بنویسید). به مثال بعدی از درسنامۀ شکل های متشابه ریاضی نهم دقت کنید.
نکته: اگر در دو مثلث متساوی‌الساقین زاویه راس برابر باشند آن دو مثلث متشابهند همچنین اگ دو زاویه مجاور قاعده هم برابر باشند باز دو مثلث متشابهند.
تشابه دو لوزی
مثال 4: آیا هر دو لوزی با یکدیگر متشابه‌اند؟
حل: مانند مثال قبل، با مثال نقض نشان می‌دهیم که هر دو لوزی لزوماً با یکدیگر متشابه نیستند (منظور از کلمۀ لزوماً این است که می‌توان لوزی‌هایی پیدا کرد که متشابه باشند اما لوزی‌هایی هم وجود دارند که متشابه نیستند). برای اینکه دو لوزی غیر متشابه مثال بزنیم، می‌توانیم از مثلث‌های متساوی‌الساقین مثال قبل استفاده کینم. اگر یک مثلث متساوی‌الساقین را نسبت به قاعده قرینه کنیم و قاعده را برداریم، یک لوزی تشکیل میشود. در شکل زیر، از قرینۀ مثلث \(\Large ABC\) مثال قبل، لوزی \(\Large ABCD\) و از قرینۀ مثلث \(\Large A’B’C’\) مثال قبل، لوزی \(\Large A’B’C’D’\) را رسم کردیم:
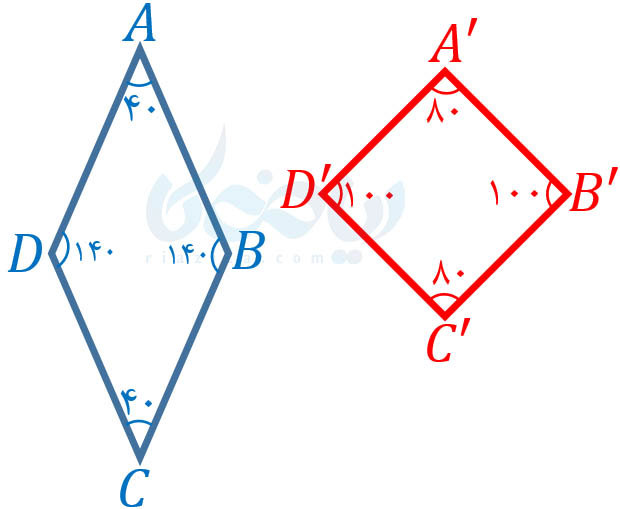
همان‌طور که می‌بینید، هیچ زاویه‌ای از لوزی \(\Large ABCD\) با هیچ زاویه‌ای از لوزی \(\Large A’B’C’D’\) برابر نیست. بنابراین این دو لوزی متشابه نیستند. به قسمت بعدی از درسنامۀ شکل های متشابه ریاضی نهم دقت کنید.
نکته: اگر یک زاویه دو لوزی با هم برابر باشند حتما آن دو لوزی متشابهند.
نسبت تشابه چیست؟
به نسبت اضلاع متناظر در دو شکل متشابه، نسبت تشابه می‌گوییم. به طور مثال، شکل زیر را در نظر بگیرید:
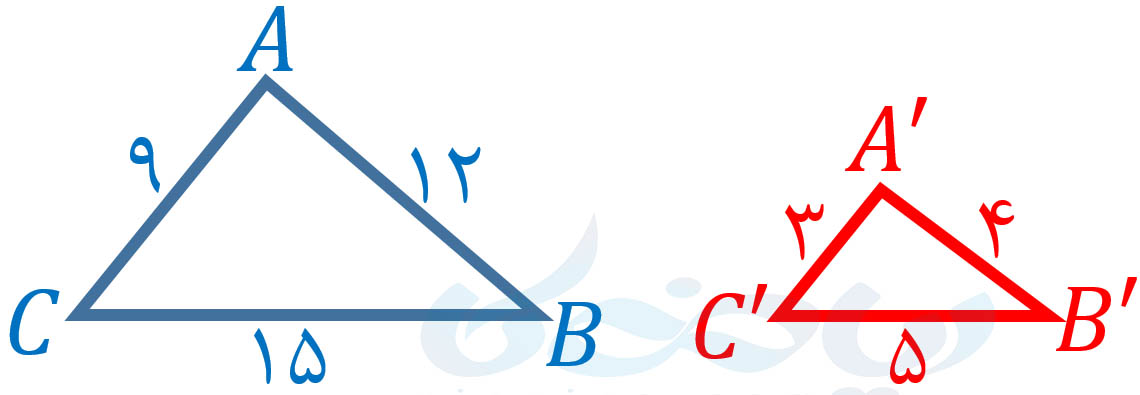
دو مثلث \(\Large ABC\) و \(\Large A’B’C’\) در شکل بالا متشابه اند. همچنین داریم:
\(\LARGE \frac{AB}{A’B’}=\frac{BC}{B’C’}=\frac{CA}{C’A’}=3\)
بنابراین نسبت تشابه مثلث \(\Large ABC\) به مثلث \(\Large A’B’C’\) برابر است با \(\Large 3\). می‌توانستیم نسبت تشابه مثلث \(\Large A’B’C’\) به مثلث \(\Large ABC\) را بیان کنیم. در این صورت می‌گفتیم نسبت تشابه مثلث \(\Large A’B’C’\) به مثلث \(\Large ABC\) برابر با \(\Large \frac{1}{3}\) است. به مثال‌های بعدی از درسنامۀ شکل های متشابه ریاضی نهم دقت کنید.
مثال از نسبت تشابه
مثال 5: مستطیل شکل زیر را در نظر بگیرید. مستطیل دیگری رسم کنید به طوری که نسبت تشابه این دو مستطیل برابر با \(\Large 2\) باشد.
حل: از آنجاییکه در صورت مسئله گفته نشده که نسبت تشابه کدام یک به دیگری برابر با \(\Large 2\) است، هم می‌توانیم نسبت تشابه مستطیل مسئله به مستطیلی که رسم می‌کنیم را برابر با \(\Large 2\) بگیریم و هم بر عکس. بنابراین مسئله دو جواب دارد، یک مستطیل کوچکتر و یک مستطیل بزرگتر که در شکل زیر رسم کرده‌ایم:
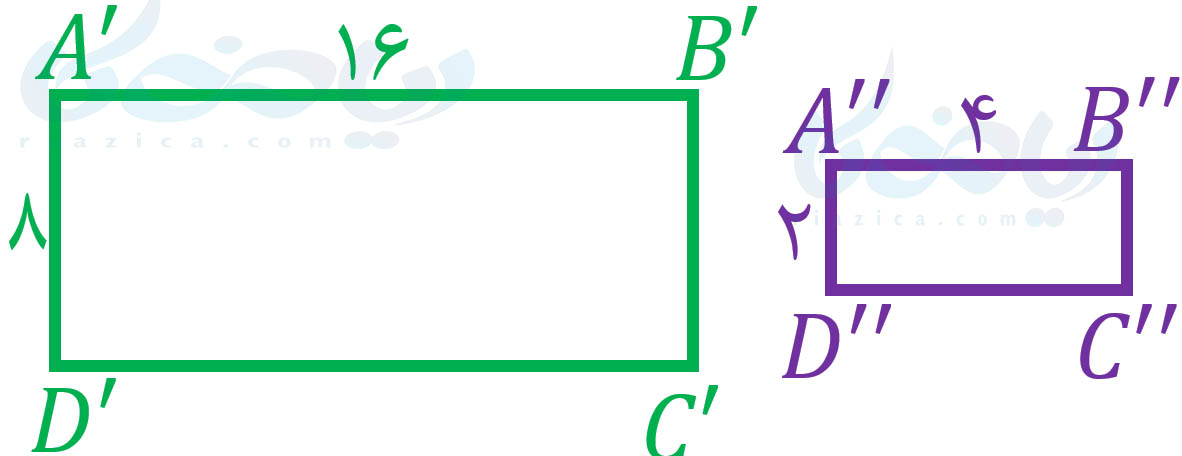
نسبت تشابه مستطیل \(\Large A’B’C’D’\) به مستطیل \(\Large ABCD\) برابر با \(\Large 2\) است. نسبت تشابه مستطیل \(\Large A”B”C”D”\) به مستطیل \(\Large ABCD\) برابر با \(\Large \frac{1}{2}\) است (به عبارت دیگر نسبت تشابه مستطیل \(\Large ABCD’\) به مستطیل \(\Large A”B”C”D”\) برابر با \(\Large 2\) است). به مثال بعدی از درسنامۀ شکل های متشابه ریاضی نهم دقت کنید.
مثال مهم از نسبت تشابه در شکل های متشابه ریاضی نهم
مثال 6: در شکل زیر، \(\Large \hat{A}=\hat{D}\) و \(\Large \hat{B}=\hat{C}\) است و دو مثلث \(\Large MBA\) و \(\Large NCD\) با یکدیگر متشابه هستند. با توجه به اندازه‌های روی شکل، اندازۀ \(\Large CN\) و \(\Large DN\) را به دست آورید.
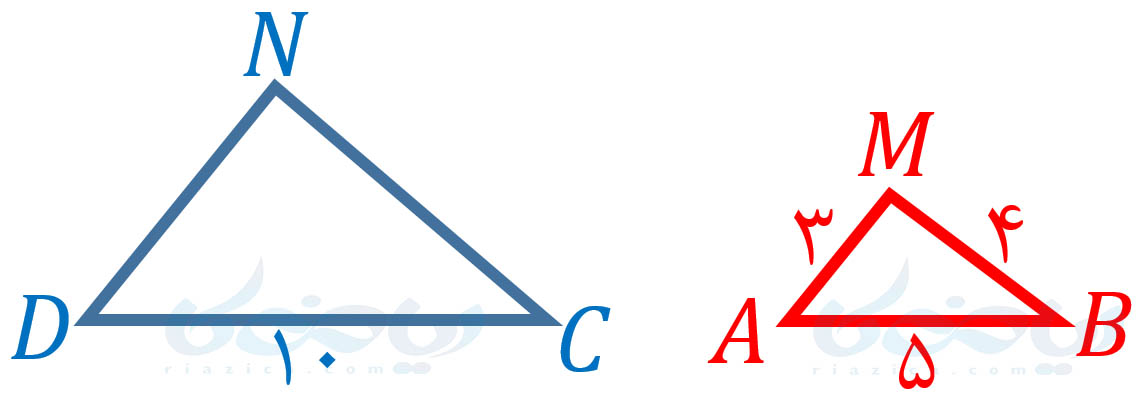
حل: اضلاع رو به رو به زوایای برابر، با یکدیگر متناظرند. بنابراین با دانستن زوایای برابر می‌توانیم تشخیص دهیم هر ضلع از مثلث \(\Large MBA\) با کدام ضلع از مثلث \(\Large NCD\) متناظر است. مثلاً چون \(\Large MA\) روبه روی زوایۀ \(\Large B\) است و \(\Large ND\) روبه روی زوایۀ \(\Large C\) است و دو زاویۀ \(\Large B\) و \(\Large C\) با هم برابرند، \(\Large MA\) و \(\Large ND\) با یکدیگر متناظرند. به همین ترتیب، \(\Large MB\) و \(\Large NC\) نیز با یکدیگر متناظرند. تنها دو ضلع \(\Large AB\) و \(\Large DC\) می‌مانند که با توجه به تشابه دو مثلث، این دو نیز با یکدیگر متناظرند. در نتیجه داریم:
\(\LARGE \frac{AB}{DC}=\frac{AM}{DN}=\frac{BM}{CN}\)
از آنجاییکه \(\Large \frac{AB}{DC}=\frac{1}{2}\) است، در نتیجه داریم:
\(\LARGE \frac{AM}{DN}=\frac{1}{2}\)
\(\LARGE \Rightarrow \frac{3}{DN}=\frac{1}{2}\)
\(\LARGE \Rightarrow DN=6\)
همین‌طور برای پیدا کردن \(\Large CN\) داریم:
\(\LARGE \frac{BM}{CN}=\frac{1}{2}\)
\(\LARGE \Rightarrow \frac{4}{CN}=\frac{1}{2}\)
\(\LARGE \Rightarrow CN=8\)
زنگ آخر کلاس شکل های متشابه ریاضی نهم
در این درسنامه از ریاضی نهم مفهوم تشابه بین چند‌ضلعی‌ها را توضیح دادیم. دو شرط برای تشابه دو چند ضلعی وجود داشت که این دو شرط را بررسی کردیم. همچنین، نسبت تشابه را تعریف کرده و مثال‌های مختلفی از اشکال متشابه حل کردیم.
ما در ریاضیکا آماده‌ی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث شکل های متشابه ریاضی نهم دارید، در دیدگاه‌ها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.
دوشکل متشابه روبه رو را در نظر بگیرید
با سلام و عرض ادب
متاسفانه متوجه سوالتون نشدم. یکبار دیگه بفرمایید.
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام درسنامه تون خیلی خوب بود میخواستم بدونم دو مستطیل دلخواه با هم متشابه نیستند.. درسته؟
سلام وادب وممنون از نظر لطف شما
بله چون اضلاعها هم باید متناسب باشد
بله
سلام خوب بود
با سلام واحترام
ممنون از حسن نظر شما
سلام
سوالی هست که میگه یک مثلث دیگه با نسبت تشابه ½ در جدول زیر بکشید، این مسئله چند جواب دارد؟
با توجه به نسبت تشابه ثابت مسئله قاعدتا باید یک جواب داشته باشه درسته؟ یا اینکه دوران و چرخش اون شکل رو باید در نظر بگیریم؟ که بشه بی نهایت؟
با سلام وادب
این سوال مانند مثال ۵ است پس دوجواب دارد.
مممممنووون
سلام
خواهش میکنم
با سلام وادب
این سوال مانند مثال ۵ است پس دوجواب دارد.
سلام دو شکل نیم دایره متشابه هستند؟ چرا؟
بله چون شعاعها به یک نسبت تغییر کرده اند
سلام یه سوالهایی هستند که مثلا میگه اگر نسبت تشابه دو مستطیل 2 به روی رادیکال ۵ باشد نسبت مساحت انها چقدر است؟
میشه لطفا راهنمایی کنید که سوالات این چنینی رو چطوری حل کنیم؟
با سلام و ادب
اگه نسبت تشابه رو k بگیریم پس نسبت طولها وعرضها به هم نیز k است چون مساحت طول ضربدر عرض هست پس نسبت مساحت ها به هم میشود kبه توان دو اما نسبت محیطها همان k میشود
عالی بود👌👌👌👌
استفاده کردیم
خیلی خوب احسنت
با سلام واحترام
ممنون از نظر لطف شما همکار محترم ویدیو های ما را در آپارات دنبال کنید ومعرف ما به دانش آموزان باشید متشکرم