آموزش ریاضی پایه نهم
اعداد گویا ریاضی نهم 📶➗ – از بزرگ به کوچک بچین!
در مبحث اعداد گویا ریاضی نهم به مباحث بسیار ساده و بسیار جذاب زیر میپردازیم:
- پیدا کردن کسر بین دو کسر
- نمایش اعشاری اعداد گویا
- مرتب کردن کسرها
هر سه مبحث بسیار جالب هستند. با حل مثالهایی که در ادامه خواهید دید، بر مطالب این مبحث به سادگی مسلط میشوید. با ما همراه باشید.
پیدا کردن کسر بین دو کسر
اگر دو کسر داشتیم و میخواستیم بین آن دو، کسر دیگری بیابیم، باید چه کار کنیم؟ روشهای مختلفی وجود دارد. در ادامه با حل مثال، دو روش را نشان خواهیم داد.
روش اول: ضرب صورت و مخرج در عدد ثابت در اعداد گویا ریاضی نهم
فرض کنید دو کسر \(\Large \frac{1}{5} \) و \(\Large \frac{2}{5} \) داده شده و میخواهیم کسری بین آنها پیدا کنیم. اگر صورت و مخرج هر دو کسر را در \(\Large 2 \) ضرب کنیم، مقدار کسرها تغییری نکرده و کسرهای \(\Large \frac{2}{10} \) و \(\Large \frac{4}{10} \) به دست میآیند. حال واضح است که کسر \(\Large \frac{3}{10} \) بین دو کسر \(\Large \frac{2}{10} \) و \(\Large \frac{4}{10} \) قرار دارد. فرآیندی که طی کردیم، در شکل زیر روی محور اعداد قابل مشاهده است:
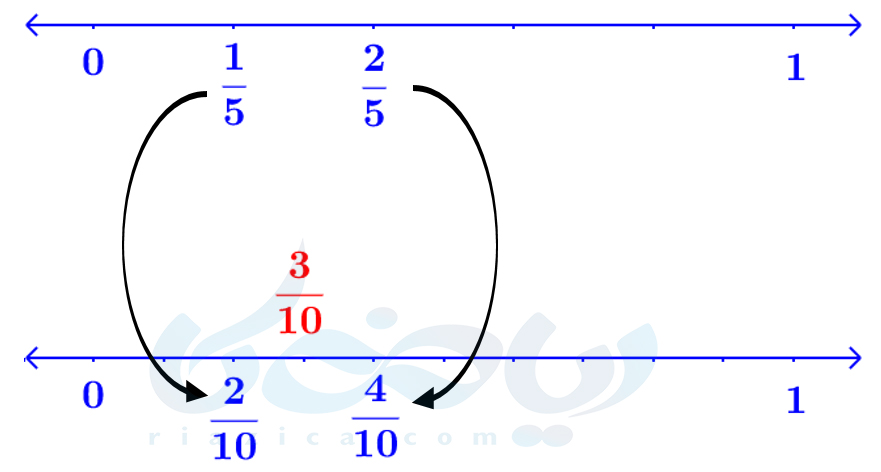
توجه کنید که به جای \(\Large 2 \) میتوان کسرها را در هر عدد دلخواهی ضرب کرد. هر چه قدر این عدد دلخواه بزگتر باشد، کسرهای بیشتری بین دو کسر داده شده میتوان پیدا کرد. به مثال زیر از مبحث اعداد گویا ریاضی نهم دقت کنید.
مثال از روش اول
مثال 1: دو کسر بین \(\Large \frac{1}{3} \) و \(\Large \frac{2}{3} \) بیابید.
حل: اگر صورت و مخرج دو کسر را در \(\Large 3 \) ضرب کنیم، دو کسر \(\Large \frac{3}{9} \) و \(\Large \frac{6}{9} \) به دست میآیند. حال به وضوح، دو کسر \(\Large \frac{4}{9} \) و \(\Large \frac{5}{9} \)، بین دو کسر \(\Large \frac{3}{9} \) و \(\Large \frac{6}{9} \) قرار دارند.
روش دوم: محاسبۀ میانگین در اعداد گویا ریاضی نهم
اگر میانگین دو کسر را محاسبه کنیم، به کسری خواهیم رسید که بین دو کسر اولیه قرار دارد. اگر به دنبال تعداد بیشتری کسر بین دو کسر اولیه باشیم، کافی است میانگین کسر به دست آمده را با یکی از دو کسر اولی حساب کنیم. با تکرار مجدد این کار برای کسرهای به دست آمده، به کسرهای جدیدی دست خواهیم یافت. به مثال زیر از مبحث اعداد گویا ریاضی نهم دقت کنید.
مثال از روش دوم
مثال 2: کسری بین \(\Large \frac{1}{3} \) و \(\Large \frac{2}{3} \) بیابید.
حل: اگر میانگین دو کسر داده شده را حساب کنیم، خواهیم داشت:
\(\LARGE\frac{\frac{1}{3}+\frac{2}{3}}{2}=\frac{3}{6}=\frac{1}{2} \)
کسر \(\Large \frac{1}{2} \) بین دو کسر \(\Large \frac{1}{3} \) و \(\Large \frac{2}{3} \) قرار دارد. به مثال زیر از مبحث اعداد گویا ریاضی نهم دقت کنید.
مثال 3: سه کسر بین کسرهای \(\Large \frac{1}{5} \) و \(\Large \frac{2}{5} \) بیابید.
حل: میانگین کسرهای \(\Large \frac{1}{5} \) و \(\Large \frac{2}{5} \) برابر است با:
\(\LARGE\frac{\frac{1}{5}+\frac{2}{5}}{2}=\frac{3}{10} \)
پس، کسر \(\Large \frac{3}{10} \) بین \(\Large \frac{1}{5} \) و \(\Large \frac{2}{5} \) قرار دارد که در محور زیر نیز قابل مشاهده است:
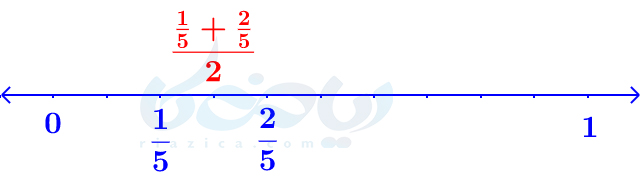
حال به محور اعداد در شکل بالا دقت کنید. اگر میانگین \(\Large \frac{1}{5} \) و \(\Large \frac{3}{10} \) را حساب کنیم، کسری بین \(\Large \frac{1}{5} \) و \(\Large \frac{3}{10} \) به دست میآید. اگر میانگین \(\Large \frac{3}{10} \) و \(\Large \frac{2}{5} \) را حساب کنیم، کسری بین \(\Large \frac{3}{10} \) و \(\Large \frac{2}{5} \) به دست می آید. در نتیجه، دو کسر جدید خواهیم داشت که بین \(\Large \frac{1}{5} \) و \(\Large \frac{2}{5} \) است. این دو کسر را مطابق آنچه گفتیم به دست میآوریم:
\(\LARGE\frac{\frac{1}{5}+\frac{3}{10}}{2}=\frac{5}{20} \)
\(\LARGE\frac{\frac{3}{10}+\frac{2}{5}}{2}=\frac{7}{10} \)
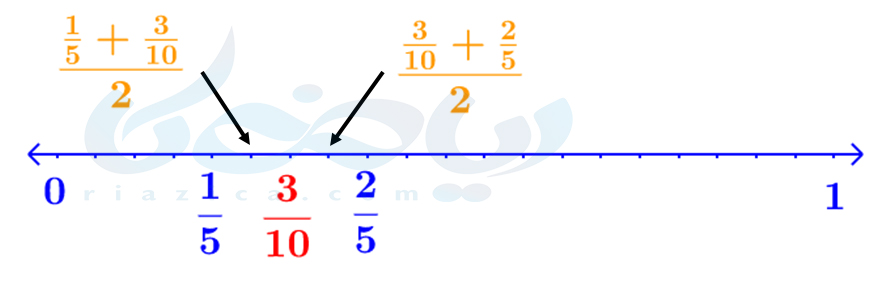
نمایش این کسرها روی محور اعداد به صورت زیر است:
اعداد گویا چیستند؟
با اعداد گویا در پایۀ هشتم آشنا شدهاید. در صورتی که مطالب مربوط به اعداد گویا در پایۀ هشتم را فراموش کردهاید، درسنامۀ تعریف اعداد گویا را مرور کنید. مجموعۀ اعداد گویا برابرند با:
\(\LARGE \mathbb{Q}=\{\frac{a}{b}|a,b \in \mathbb{Z}, b\neq 0\}\)
یعنی مجموعۀ اعداد گویا برابر است با مجموعۀ کسرهایی که صورت و مخرج آن عدد صحیح بوده و مخرج آن مخالف صفر است. مطابق آنچه در قسمت قبل گفتیم، بین هر دو کسر میتوان به تعداد دلخواه کسر جدید پیدا کرد. بنابراین، مجموعۀ اعداد گویا نامتناهی است (لازم به ذکر است که اعداد گویا با وجود نامتناهی بودن، شمارش پذیرند. در صورتی که علاقه دارید، میتوانید اثبات شمارشپذیر بودن اعداد گویا را ماطلعه کنید).
نمایش اعشاری اعداد گویا
در سالهای گذشته با نمایش اعشاری کسرها آشنا شده اید. نمایش اعشاری کسر \(\Large \frac{1}{2} \)، عدد اعشاری 0/5 است. همانطور که دیدید، نمایش اعشاری کسر \(\Large \frac{1}{2} \) متناهی یا به عبارت دیگر مختوم است. اما همۀ کسرها این طور نیستند. مثلاً اگر بخواهیم نمایش اعشاری کسر \(\Large \frac{1}{3} \) را بنویسیم، بعد از 0 و ممیز باید نامتناهی 3 قرار دهیم. از آنجاییکه نمیتوانیم نامتناهی 3 بنویسیم، نمایش اعشاری کسر \(\Large \frac{1}{3} \) به صورت زیر در میآید:
\(\LARGE \frac{1}{3}=0.333\dots=0.\bar{3} \)
خط بالای عد 3 به این معنی است که این عدد به صورت نامتناهی تکرار میشود. اصطلاحاً به این اعداد اعشاری، اعداد اعشاری متناوب میگوییم؛ زیرا یک یا چند رقم (که همۀ آنها برابر باصفر نیستند) در این اعداد اعشاری به صورت نامتناهی تکرار میشوند. به مثال زیر از مبحث اعداد گویا ریاضی نهم دقت کنید.
مثال از اعداد اعشاری متناوب
مثال 4: نمایش اعشاری کسر \(\Large \frac{5}{11} \) را بنویسید.
حل: برای پیدا کردن نمایش اعشاری کسر \(\Large \frac{5}{11} \) باید عدد 5 را بر 11 تقسیم کنیم. در این صورت بعد از رقم 0 و ممیز، دو رقم 4 و 5 به صورت نامتناهی تکرار میشوند. یعنی داریم:
\(\LARGE \frac{5}{11}=0.454545\dots\)
بنابراین نمایش اعشاری کسر \(\Large \frac{5}{11} \) به صورت \(\Large 0.\bar{45} \) است.
مرتب کردن کسرها
روشهای متفاوتی برای مرتب کردن کسرها از کوچک به بزرگ یا برعکس وجود دارد. میتوانیم نمایش اعشاری کسرها را نوشته و آن ها را با یکدیگر مقایسه کنیم. همچنین، میتوانیم مخرج کسرها را یکی کرده و صورت آنها را مقایسه کنیم. در ادامه، با حل مثال از مبحث اعداد گویا ریاضی نهم این دو روش را بررسی میکنیم.
مرتب کردن کسرها با یکی کردن مخرج
مثال 5: اعداد کسری \(\Large \frac{2}{3} \) و \(\Large \frac{1}{4} \) و \(\Large \frac{3}{5} \) را مرتب کنید.
حل: کوچکترین مضرب مشترک مخرج سه کسر برابر است با \(\Large 60 \). با ضرب صورت و مخرج هر کسر در یک عدد ثابت، مخرج سه کسر را یکی و برابر با 60 میکنیم:
\(\LARGE \frac{2}{3}=\frac{40}{60}\)
\(\LARGE \frac{1}{4}=\frac{15}{60}\)
\(\LARGE \frac{3}{5}=\frac{36}{60}\)
بنابراین ترتیب این سه کسر به صورت زیر است:
\(\LARGE \frac{1}{4}<\frac{3}{5}<\frac{2}{3}\)
مرتب کردن کسرها با نمایش اعشاری
میتوانستیم مثال 5 را با استفاده از نمایش اعشاری کسرها نیز حل کنیم. نمایش اعشاری سه کسر \(\Large \frac{2}{3} \) و \(\Large \frac{1}{4} \) و \(\Large \frac{3}{5} \) به صورت زیر است:
\(\LARGE \frac{2}{3}=0.\bar{6}\)
\(\LARGE \frac{1}{4}=0.25\)
\(\LARGE \frac{3}{5}=0.6\)
واضح است که عدد اعشاری 0.25 از دو عدد اعشاری دیگر کوچکتر است. در عدد اعشاری \(\Large 0.\bar{6} \)، بعد از رقم صفر، ممیز و رقم شش، نا متناهی رقم شش دیگر داریم؛ اما در عدد اعشاری \(\Large 0.6 \)، بعد از رقم صفر، ممیز و رقم شش، رقم دیگری نداریم. یا به عبارت دیگر رقمهای بعدی صفر است. بنابراین عدد اعشاری \(\Large 0.\bar{6} \) از \(\Large 0.6 \) بزرگتر است.
توجه اعداد گویا ریاضی نهم: شما عزیران میتوانید اعمال بین اعداد گویا را در ریاضی هشتم مطالعه کنید.
زنگ آخر کلاس اعداد گویا ریاضی نهم
مبحث بسیار جالبی از ریاضی نهم بود! از پیدا کردن کسر بین دو کسر گرفته تا نمایش اعشاری مختوم و متناوب. برای پیدا کردن کسر بین دو کسر دو روش گفتیم و از هر کدام مثال حل کردیم. نمایش اعشاری اعداد گویا و مرتب کردن کسرها نیز مباحث بسیار سادهای بودند که با حل مثال از هریک، به مفهوم آنها مسلط شدیم.یادتون نره رمز موفقیت در درس ریاضی تمرین وتکرار وتکرار هست.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث اعداد گویا ریاضی نهم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





خعلی خوب توضیح دادین ممنون
با سلام وعرض ادب
ممنون از لطف شما دوست عزیز
آره واقعا عالی بود ممنون
با سلام وعرض ادب
خدا رو شکر که برای شما مفید واقع شده.
واقعا همیشه خیلی خوب توضیح میدین شما نباشبم من صفر میگیرم تو امتحان
با سلام واحترام
خوشحالیم که سایت ما برای شما مفیدهست
خیلی خوب بود ممنون
بعد ما میتونیم سر جلسه امتحان ماشین حساب داشته باشیم؟
با سلام واحترام
نه متاسفانه
سلام میشه بین دو کسر. جواب را از بزرگ به کوچک بنویسیم؟
35\100و 34/۱٠٠و 33/۱٠٠. ۳۲/۱٠٠
۳۱/۱٠٠. ۳٠ /۱٠٠
یعنی از بزرگ به کوچک بنویسیم
با سلام
بستگی داره سوال چطوری خواسنه
عالی خیلی ممنون.
با سلام وممنون از نگاه شما
واقعا عالی مث همیشه
با سلام وادب
ممنون از شما که باعث دلگرمی ما برای ادامه راه هستید
خوب بود من تازه اومدم دیدم استادمون بهمون گفته در مورد اعداد گویا تحقیق کنم اومد تا اینکه سایت شما رو دیدم خیلی عالی بود?
با سلام وقت به خیر
خدا رو شکر که مطالب سایت برای شما مفید بوده
سلام وقت بخیر مجموعه عدد گویا به نماد ریاضی چی میشه؟
با سلام وادب
مجموعه گویا را با حرف Q نشان می دهند و به صورت کسر a/b که b مخالف صفر هست
سلام میشه به من کمک کنید
سلام دوست عزیز چه کمکی از دست ما بر میاد؟