محاسبات عبارت های گویا نهم 📝➗ – اعمال ریاضی شو یادبگیر!

در درسنامهٔ محاسبات عبارت های گویا نهم سه مبحث اصلی زیر را بررسی می‌کنیم:

• ضرب و تقسیم عبارت های گویا
• جمع و تفریق عبارت های گویا
• ساده کردن عبارت های مرکب

همان طور که خواهید دید، برای جمع و تفریق عبارت‌های گویا نیاز خواهیم داشت که مخرج مشترک دو عبارت گویا را محاسبه کنیم. به همین خاطر قسمتی از درسنامه را به روش پیدا کردن ک.م.م دو عبارت جبری جهت محاسبهٔ مخرج مشترک اختصاص خواهیم داد. توصیه می‌کنیم قبل از مطالعهٔ این درسنامه، درسنامهٔ معرفی عبارت گویا نهم را مرور کنید. با ما تا انتهای درسنامهٔ محاسبات عبارت های گویا نهم همراه باشید.

---

---

ضرب و تقسیم عبارت های گویا

ضرب و تقسیم عبارت‌های گویا مشابه با ضرب و تقسیم اعداد گویا صورت می‌گیرد. همان طور که به خاطر دارید، ضرب دو عدد گویا به صورت زیر انجام می‌شد (مخرج کسرهای زیر مخالف صفر هستند):

\(\LARGE \frac{m}{n} \times \frac{p}{q}=\frac{mp}{nq}\)

به عبارت دیگر برای ضرب دو عدد گویا باید صورت‌ها را در هم و مخرج‌ها را در هم ضرب می‌کردیم. برای عبارت های گویا نیز، باید دقیقاً همین کار را انجام دهیم. در مورد تقسیم نیز، همین شباهت وجود دارد. برای تقسیم دو عدد گویا به صورت زیر عمل می‌کردیم (مخرج کسرهای زیر مخالف صفر هستند):

\(\LARGE \frac{m}{n} \div \frac{p}{q}=\frac{m}{n} \times \frac{q}{p}=\frac{mq}{np}\)

به عبارت دیگر، زمانی که یک کسر را بر کسر دیگری تقسیم می‌کردیم، جای صورت و مخرج کسر دوم را برعکس کرده و سپس دو کسر را در هم ضرب می‌کنیم. تقسیم عبارات گویا نیز به همین صورت انجام می‌شود. مشابه اعداد گویا، برای عبارات گویا نیز لازم است که کسرها را قبل یا بعد از محاسبات ساده کنیم. برای ساده سازی عبارات گویا گاهی لازم است از آموخته‌هایمان در درسنامهٔ تجزیه ریاضی نهم استفاده کنیم. پیشنهاد می‌کنیم اگر تجزیهٔ عبارت‌های جبری را فراموش کرده‌اید، این درسنامه را مرور کنید. برای اینکه با ضرب و تقسیم عبارت های گویا بیشتر آشنا شوید، به مثال‌های بعدی از درسنامهٔ محاسبات عبارت های گویا نهم توجه کنید.

مثال از ضرب عبارت های گویا

مثال 1: حاصل عبارت \(\Large \frac{3x}{yz} \times \frac{z^3}{6x^2}\) را به دست آورید.

حل: بهتر است قبل از محاسبهٔ عبارت، آن را ساده کنیم. برای ساده سازی عبارت داده شده، اقدامات زیر را انجام می‌دهیم:

• عبارت \(\Large x\) در صورت کسر اول را با عبارت \(\Large x^2\) در مخرج کسر دوم ساده می‌کنیم؛ به این ترتیب، \(\Large x\) در مخرج کسر دوم باقی می‌ماند.
• عبارت \(\Large z^3\) از صورت کسر دوم را با عبارت \(\Large z\) از مخرج کسر اول ساده می‌کنیم؛ در این صورت، عبارت \(\Large z^2\) در صورت کسر دوم باقی می‌ماند.
• عدد \(\Large 3\) ار صورت کسر اول را با عدد \(\Large 6\) از مخرج کسر دوم ساده می‌کنیم؛ به این ترتیبب، عدد \(\Large 2\) در مخرج کسر دوم باقی می‌ماند.

برای اینکه بهتر متوجه شوید، هر جفت عبارتی را که با یکدیگر ساده می‌کنیم، با یک رنگ خط می‌زنیم:

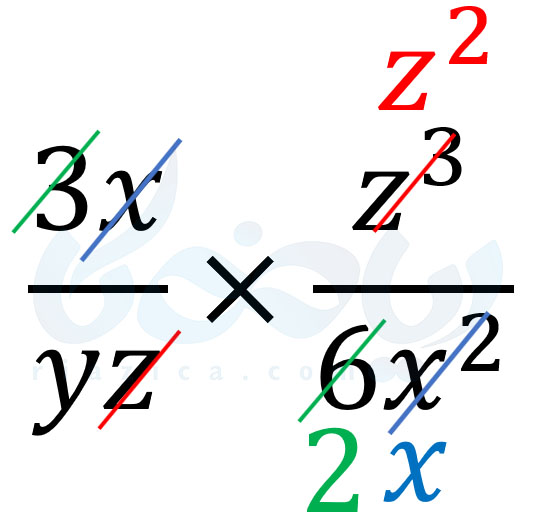
برای به دست آوردن حاصل ضرب دو عبارت کافی است عباراتی که در صورت دو کسر باقی مانده را در هم و عباراتی که در مخرج دو کسر باقی مانده را در هم ضرب کنیم. در صورت کسر اول، عدد \(\Large 1\) و در صورت کسر دوم، عبارت \(\Large z^2\) باقی مانده است. از ضرب این دو، عبارت \(\Large z^2\) به دست می‌آید. در مخرج کسر اول، عبارت \(\Large y\) و در مخرج کسر دوم، عبارت \(\Large 2x\) باقی مانده است. از ضرب این دو، عبارت \(\Large 2xy\) حاصل می‌شود. به این ترتیب داریم:

\(\LARGE \frac{3x}{yz} \times \frac{z^3}{6x^2}\)

\(\LARGE =\frac{1}{y} \times \frac{z^2}{2x}\)

\(\LARGE =\frac{z^2}{2xy}\)

به مثال بعدی از درسنامهٔ محاسبات عبارت های گویا نهم توجه کنید.

مثال از ضرب عبارت های گویا

مثال 2: حاصل عبارت \(\Large \frac{x}{x+2} \times \frac{x^2+6x+8}{x^3}\) را به دست آورید.

حل: ابتدا صورت کسر دوم را با استفاده از اتحاد جمله مشترک تجزیه می‌کنیم (اگر تجزیه با استفاده از اتحاد جمله مشترک را فراموش کرده‌اید، درسنامهٔ تجزیه ریاضی نهم را مرور کنید):

\(\LARGE \frac{x}{x+2} \times \frac{x^2+6x+8}{x^3}\)

\(\LARGE =\frac{x}{x+2} \times \frac{(x+2)(x+4)}{x^3}\)

حال باید ساده‌سازی کنیم. عبارت \(\Large (x+2)\) هم در مخرج کسر اول و هم در صورت کسر دوم وجود دارد. بنابراین از هر دو کسر ساده می‌شود. عبارت \(\Large x\) از صورت کسر اول با عبارت \(\Large x^3\) از مخرج کسر دوم ساده شده و \(\Large x^2\) در مخرج کسر دوم باقی می‌ماند. به این ترتیب داریم:

\(\LARGE \frac{x}{x+2} \times \frac{(x+2)(x+4)}{x^3}\)

\(\LARGE =\frac{1}{1} \times \frac{(x+4)}{x^2}\)

\(\LARGE  =\frac{(x+4)}{x^2}\)

به مثال بعدی از درسنامهٔ محاسبات عبارت های گویا نهم توجه کنید.

مثال از تقسیم عبارات گویا

مثال 3: حاصل عبارت \(\Large \frac{x^2-9}{x^2+4x+3} \div \frac{x^2-6x+9}{x+5}\) را به دست آورید.

حل: تقسیم عبارات گویا نکتهٔ جدیدی نسبت به ضرب آن‌ها ندارد. کافی است، جای صورت و مخرج کسر دوم را عوض کرده و سپس دو کسر را در هم ضرب کنیم. یعنی داریم:

\(\LARGE \frac{x^2-9}{x^2+4x+3} \div \frac{x^2-6x+9}{x+5}\)

\(\LARGE =\frac{x^2-9}{x^2+4x+3} \times \frac{x+5}{x^2-6x+9}\)

بقیهٔ مراحل حل مسئله، مانند مثال 1 و 2 است. یعنی ابتدا باید عبارت را ساده کرده و سپس در هم ضرب کنیم. برای ساده سازی، باید صورت کسر اول را با استفاده از اتحاد مزدوج، مخرج کسر اول را با استفاده از اتحاد جمله مشترک و مخرج کسر دوم را با استفاده از اتحاد مربع دو جمله‌ای تجزیه کنیم (تجزیه با استفاده از اتحاد‌های مختلف، در درسنامهٔ تجزیه ریاضی نهم توضیح داده شده):

\(\LARGE \frac{x^2-9}{x^2+4x+3} \times \frac{x+5}{x^2-6x+9}\)

\(\LARGE =\frac{(x-3)(x+3)}{(x+1)(x+3)} \times \frac{x+5}{(x-3)^2}\)

همان طور که می‌بینید، عبارت \(\Large (x+3)\) بین صورت و مخرج کسر اول مشترک است. بنابراین ساده می‌شود. عبارت \(\Large (x-3)\) در صورت کسر اول با عبارت \(\Large (x-3)^2\) در مخرج کسر دوم ساده شده و عبارت \(\Large (x-3)\) در مخرج کسر دوم باقی می‌ماند. به این ترتیب داریم:

\(\LARGE \frac{(x-3)(x+3)}{(x+1)(x+3)} \times \frac{x+5}{(x-3)^2}\)

\(\LARGE =\frac{1}{(x+1)} \times \frac{x+5}{(x-3)}\)

\(\LARGE =\frac{x+5}{(x+1)(x-3)}\)

به قسمت بعدی از درسنامهٔ محاسبات عبارت های گویا نهم توجه کنید.

جمع و تفریق عبارت ‌های گویا

جمع و تفریق عبارات گویا نیز مانند جمع و تفریق اعداد گویا صورت می‌گیرد. زمانی که می‌خواستیم دو عدد گویا را با یکدیگر جمع کنیم، ابتدا مخرج مشترک آن دو عدد را محاسبه کرده و سپس جمع و تفریق را انجام می‌دهیم. همان طور که در درسنامهٔ کوچکترین مضرب مشترک ریاضی هفتم خواندیم، مخرج مشترک دو عدد را با محاسبهٔ ک.م.م آن‌ها به دست می‌آوردیم. روش به دست آوردن ک.م.م دو عدد را آموخته‌ایم، اما پیدا کردن ک.م.م دو عبارت جبری را بررسی نکرده‌ایم. بنابراین در قسمت بعدی از درسنامهٔ محاسبات عبارت های گویا نهم ابتدا روش به دست آوردن ک.م.م دو عبارت جبری را بررسی کرده و سپس به جمع و تفریق عبارات گویا خواهیم پرداخت.

ک.م.م دو عبارت جبری

همان طور که در درسنامهٔ تعریف توان ریاضی هفتم هم دیدیم، برای یافتن ک.م.م دو عدد، ابتدا دو عدد را تجزیه کرده و سپس، هم عوامل مشترک و هم غیر مشترک را با بیشترین توان در هم ضرب می‌کریم تا ک.م.م به دست آید. به طور مثال اگر می‌خواستیم ک.م.م دو عدد \(\Large 72\) و \(\Large 84\) را پیدا کنیم، ابتدا دو عدد را به صورت حاصل ضرب عوامل اول می‌نوشتیم:

\(\LARGE 72=2^3 \times 3^2\)

\(\LARGE 84=2^2 \times 3 \times 7\)

سپس، برای به دست آوردن ک.م.م دو عدد، هم پایه‌های مشترک و هم غیر مشترک را با بیشترین توان در هم ضرب می‌کردیم. به این ترتیب داشتیم:

\(\Large [72,84]=2^3 \times 3^2 \times 7 =504\)

برای دو عبارت جبری نیز باید مشابه همین کار را انجام دهیم. تفاوت اینجاست که در عبارت‌های جبری، پایه‌های مشترک و غیر مشترک، به جای اینکه اعداد اول باشند، عبارت‌های جبری تجزیه‌ناپذیر هستند. مثلاً، عبارت \(\Large x^2-4\) را می‌توان با استفاده از اتحاد مزدوج تجزیه کرده و به صورت حاصل ضرب \(\Large (x-2)(x+2)\) نوشت. هیچ یک از عبارات \(\Large (x-2)\) یا \(\Large (x+2)\) را نمی‌توان تجزیه کرد. بنابراین اگر عبارت \(\Large x^2-4\) را به صورت حاصل ضرب \(\Large (x-2)(x+2)\) بنویسیم، آن را به عوامل تجزیه‌ناپذیر، تجزیه کرده‌ایم. برای اینکه بهتر متوجه شوید، به مثال‌های بعدی از درسنامهٔ محاسبات عبارت های گویا نهم توجه کنید.

مثال از ک.م.م عبارات جبری

مثال 4: ک.م.م دو عبارت \(\Large A=(x+3)^2(x-1)\) و \(\Large B=(x+1)^4(x+3)^3\) را محاسبه کنید.

حل: هر دو عبارت \(\Large A\) و \(\Large B\) به صورت حاصل ضرب عوامل تجزیه‌ناپذیر نوشته شده‌اند. عبارت \(\Large (x+3)\) بین هر دو مشترک است. توان عبارت \(\Large (x+3)\) در \(\Large A\) برابر با \(\Large 2\) و در \(\Large B\) برابر با \(\Large 3\) است. بنابراین، بیشترین توان آن که همان \(\Large 3\) است را در نظر می‌گیریم. عبارات \(\Large (x+1)\) و \(\Large (x-1)\) بین \(\Large A\) و \(\Large B\) مشترک نیستند. بنابراین هر یک را با توانی که دارند (که در واقع همان بیشترین توان بین دو عبارت محسوب می‌شود) در نظر می گیریم. به این ترتیب، ک.م.م \(\Large A\) و \(\Large B\) برابر است با:

\(\Large [A,B]=(x+3)^3(x+1)^4(x-1)\)

به مثال بعدی از درسنامهٔ محاسبات عبارت های گویا نهم توجه کنید.

---

---

مثال از ک.م.م عبارات جبری

مثال 5: ک.م.م دو عبارت \(\Large A=x^2+5x+6\) و \(\Large B=(x^2-4)(x+3)^3\) را محاسبه کنید.

حل: ابتدا دو عبارت را به صورت حاصل ضرب عوامل تجزیه نا‌پذیر می‌نویسیم. به این منظور، عبارت \(\Large A\) را با استفاده از اتحاد جمله مشترک تجزیه‌ می‌کنیم:

\(\LARGE A=x^2+5x+6\)

\(\LARGE =(x+2)(x+3)\)

عبارت \(\Large B\) را نیز با استفاده از اتحاد مزدوج تجزیه می‌کنیم:

\(\LARGE B=(x^2-4)(x+3)^3\)

\(\LARGE =(x-2)(x+2)(x+3)^3\)

همان طور که می‌بینید، عبارت \(\Large (x+2)\) بین \(\Large A\) و \(\Large B\) مشترک است. توان این عبارت نیز در هر دو برابر با یک است. بنابراین عبارت \(\Large (x+2)\) را با توان یک در نظر می‌گیریم. عبارت \(\Large (x+3)\) نیز بین دو عبارت مشترک است. توان آن در \(\Large A\) برابر با \(\Large 1\) و در \(\Large B\) برابر با \(\Large 3\) است. بنابراین بیشترین توان آن را که همان \(\Large 3\) است در نظر می‌گیریم. عبارت \(\Large (x-2)\) بین \(\Large A\) و \(\Large B\) مشترک نیست. بیشترین توان آن بین دو عبارت، برابر با یک است. به این ترتیب، ک.م.م \(\Large A\) و \(\Large B\) برابر است با:

\(\Large [A,B]=(x+2)(x+3)^3(x-2)\)

به قسمت بعدی از درسنامهٔ محاسبات عبارت های گویا نهم توجه کنید.

جمع و تفریق عبارت گویا با محاسبهٔ مخرج مشترک

حال که فهمیدیم ک.م.م عبارات جبری چگونه به دست می‌آید، می‌توانیم مخرج مشترک عبارات جبری را محاسبه کرده و جمع و تفریق را انجام دهیم. به مثال زیر دقت کنید.

مثال 6: حاصل عبارت \(\Large \frac{x+3}{x+4}+\frac{x^2}{x+4}\) را به دست آورید.

حل: ابتدا باید مخرج مشترک دو کسر را به دست آوریم. مخرج مشترک دو کسر برابر است با ک.م.م مخرج آن‌ها. در اینجا چون مخرج هر دو کسر برابر با \(\Large x+4\) است، ک.م.م هم همان \(\Large x+4\) می‌شود. بنابراین کافی است صورت ها را با هم جمع کرده و مخرج را همان \(\Large x+4\) قرار دهیم:

\(\LARGE \frac{x+3}{x+4}+\frac{x^2}{x+4}=\frac{x+3+x^2}{x+4}\)

به مثال بعدی از درسنامهٔ محاسبات عبارت های گویا نهم توجه کنید.

مثال از جمع عبارت های گویا

مثال 7: حاصل عبارت \(\Large \frac{x}{x^2+10x+25}+\frac{x+1}{x+5}\) را به دست آورید.

حل: ابتدا باید مخرج مشترک دو کسر را به دست آوریم. مخرج مشترک دو کسر برابر است با ک.م.م مخرج آن‌ها. برای اینکه ک.م.م مخرج دو کسر را محاسبه کنیم، ابتدا مخرج کسر اول را با استفاده از اتحاد مربع دو جمله‌ای تجزیه می‌کنیم:

\(\LARGE \frac{x}{x^2+10x+25}+\frac{x+1}{x+5}\)

\(\LARGE =\frac{x}{(x+5)^2}+\frac{x+1}{x+5}\)

ک.م.م. دو عبارت \(\Large x+5\) و \(\Large (x+5)^2\) برابر با \(\Large (x+5)^2\) است. زیرا \(\Large x+5\) بین هر دو مشترک است و بیشترین توان آن برابر با \(\Large 2\) است. چون مخرج کسر دوم در \(\Large (x+5)\) ضرب می‌شود، باید صورت کسر دوم را نیز در \(\Large (x+5)\) ضرب کرده و سپس با صورت کسر اول جمع کنیم؛ درست مانند کاری که با اعداد گویا می‌کردیم:

\(\LARGE \frac{x}{(x+5)^2}+\frac{x+1}{x+5}\)

\(\LARGE =\frac{x+(x+1)(x+5)}{(x+5)^2}\)

\(\LARGE =\frac{x+x^2+6x+5}{(x+5)^2}\)

\(\LARGE =\frac{x^2+7x+5}{(x+5)^2}\)

به مثال بعدی از درسنامهٔ محاسبات عبارت های گویا نهم توجه کنید.

مثال از تفریق عبارت های گویا

مثال 8: حاصل عبارت \(\Large \frac{2x}{x^2-4x-5}-\frac{x+4}{x^2+2x+1}\) را به دست آورید.

حل: ابتدا مخرج کسر اول را با استفاده از اتحاد جمله مشترک و مخرج کسر دوم را با استفاده از اتجاد مربع دو جمله‌ای تجزیه می‌کنیم:

\(\LARGE \frac{2x}{x^2-4x-5}-\frac{x+4}{x^2+2x+1}\)

\(\LARGE =\frac{2x}{(x+1)(x-5)}-\frac{x+4}{(x+1)^2}\)

برای محاسبهٔ مخرج مشترک باید ک.م.م دو عبارت \(\Large (x+1)(x-5)\) و \(\Large (x+1)^2\) را به دست آوریم. عبارت \(\Large (x+1)\) بین هر دو مشترک است و بیشترین توان آن برابر با \(\Large 2\) است. عبارت \(\Large (x-5)\) بین دو عبارت مشترک نبوده و توان آن برابر با \(\Large 1\) است. بنابراین، مخرج مسترک که همان ک.م.م است، برابر است با \(\Large (x+1)^2(x-5)\). پس، صورت کسر اول را در \(\Large (x+1)\) و صورت کسر دوم را در \(\Large (x-5)\) ضرب کرده و دو عبارت را تفریق می‌کنیم:

\(\LARGE \frac{2x}{(x+1)(x-5)}-\frac{x+4}{(x+1)^2}\)

\(\LARGE =\frac{2x(x+1)-(x+4)(x-5)}{(x+1)^2(x-5)}\)

\(\LARGE =\frac{2x^2+2x-x^2+x+20}{(x+1)^2(x-5)}\)

\(\LARGE =\frac{x^2+3x+20}{(x+1)^2(x-5)}\)

به مثال بعدی از درسنامهٔ محاسبات عبارت های گویا نهم توجه کنید.

مثال از تفریق دو عبارت گویا

مثال 9: حاصل عبارت \(\Large \frac{x-1}{x+4}-\frac{x+6}{x+1}\) را به دست آورید.

حل: ابتدا باید مخرج مشترک دو کسر را به دست آوریم. مخرج مشترک دو کسر برابر است با ک.م.م مخرج آن‌ها. هیچ عبارتی بین مخرج دو کسر مشترک نیست. بنابراین ک.م.م مخرج کسرها برابر است با حاصل ضرب آن‌ها؛ یعنی برابر است با \(\Large (x+4)(x+1)\). درنتیجه باید صورت کسر اول را در \(\Large (x+1)\) و صورت کسر دوم را در \(\Large (x+4)\) ضرب کرده و آن‌ها را تفریق کنیم:

\(\LARGE \frac{x-1}{x+4}-\frac{x+6}{x+1}\)

\(\LARGE =\frac{(x-1)(x+1)-(x+6)(x+4)}{(x+4)(x+1)}\)

\(\LARGE =\frac{x^2-1-x^2-10x-24}{(x+4)(x+1)}\)

\(\LARGE =\frac{-10x-25}{(x+4)(x+1)}\)

به قسمت بعدی از درسنامهٔ محاسبات عبارت های گویا نهم توجه کنید.

ساده کردن عبارت های مرکب

اگر در صورت یا مخرج یک عبارت گویا، عبارت گویای دیگری وجود داشته باشد، اصطلاحاً به آن عبارت، عبارت مرکب می‌گوییم. مثلاً، عبارت \(\Large \frac{\frac{x+4}{x^2+5}}{y}\)، عبارت مرکب است؛ زیرا عبارت گویایی است که در صورت آن یک عبارت گویای دیگر وجود دارد. برای محاسبهٔ عبارت‌های مرکب، دو کار می‌توان انجام داد:

• روش اول: صورت و مخرج را به صورت جداگانه ساده کرده و سپس بر هم تقسیم کرد.
• روش دوم: صورت و مخرج را در یک عبارت ضرب کرده تا کسر از حالت مرکب خارج شود. سپس، عبارت به دست آمده را ساده کرد.

چگونگی استفاده از هر یک از این دو روش را در حل دو مثال بعدی از درسنامهٔ محاسبات عبارت های گویا نهم نشان می‌دهیم.

مثال از ساده کردن عبارت های مرکب

مثال 10: حاصل عبارت \(\Large \frac{-x+\frac{x^2}{x+3}}{\frac{-x^2}{x^2-9}+1}\) را به دست آورید.

حل: از روش اولی که گفتیم استفاده می‌کنیم. یعنی صوررت و مخرج را به صورت جداگانه ساده کرده و سپس بر یکدیگر تقسیم می‌کنیم. ساده سازی صورت و مخرج به صورت زیر انجام می‌شود:

\(\LARGE \frac{-x+\frac{x^2}{x+3}}{\frac{-x^2}{x^2-9}+1}\)

\(\LARGE =\frac{\frac{-x(x+3)+x^2}{x+3}}{\frac{-x^2+(x^2-9)}{x^2-9}}\)

\(\LARGE =\frac{\frac{-x^2-3x+x^2}{x+3}}{\frac{-x^2+x^2-9}{x^2-9}}\)

\(\LARGE =\frac{\frac{-3x}{x+3}}{\frac{-9}{x^2-9}}\)

\(\LARGE =\frac{-3x}{x+3}\div \frac{-9}{x^2-9}\)

\(\LARGE =\frac{-3x}{x+3}\times \frac{x^2-9}{-9}\)

حال باید صورت کسر دوم را با استفاده از اتحاد مزدوج تجزیه کنیم:

\(\LARGE \frac{-3x}{x+3}\times \frac{x^2-9}{-9}\)

\(\LARGE =\frac{-3x}{x+3}\times \frac{(x-3)(x+3)}{-9}\)

همان طور که می‌بینید، عبارت \(\Large (x+3)\) هم در مخرج کسر اول و هم در صورت کسر دوم وجود دارد. بنابراین آن را ساده می‌کنیم. اعداد \(\Large -3\) و \(\Large -9\) را نیز با هم ساده می‌کنیم:

\(\LARGE \frac{-3x}{x+3}\times \frac{(x-3)(x+3)}{-9}\)

\(\LARGE =\frac{x}{1}\times \frac{(x-3)}{3}\)

\(\LARGE =\frac{x(x-3)}{3}\)

به مثال بعدی از درسنامهٔ محاسبات عبارت های گویا نهم توجه کنید.

مثال از ساده کردن عبارت های مرکب

مثال 11: حاصل عبارت \(\Large \frac{\frac{3}{x}-\frac{2}{x-1}}{\frac{-1}{x-1}+\frac{2}{x}}\) را به دست آورید.

حل: برای حل این مسٔله از روش دوم استفاده می‌کنیم. یعنی صورت و مخرج کسر را در عبارتی ضرب می‌کنیم که مخرج کسر‌ها ساده شوند. در این مثال، اگر صورت و مخرج کسر را در عبارت \(\Large x(x-1)\) ضرب کنیم، مخرج‌ها ساده می‌شوند:

\(\LARGE \frac{\frac{3}{x}-\frac{2}{x-1}}{\frac{-1}{x-1}+\frac{2}{x}}=\frac{x(x-1)(\frac{3}{x}-\frac{2}{x-1})}{x(x-1)(\frac{-1}{x-1}+\frac{2}{x})}\)

\(\LARGE =\frac{x(x-1) \times \frac{3}{x}- x(x-1) \times \frac{2}{x-1}}{x(x-1) \times \frac{-1}{x-1}+x(x-1) \times\frac{2}{x}}\)

\(\LARGE =\frac{3(x-1)- 2x}{-x+2(x-1)}\)

\(\LARGE =\frac{3x-3-2x}{-x+2x-2}\)

\(\LARGE =\frac{x-3}{x-2}\)

به قسمت بعدی از درسنامهٔ محاسبات عبارت های گویا نهم توجه کنید.

حل مسئله با استفاده از عبارت های گویا

از تمام مطالبی که در این درسنامه آموختیم، می‌توان برای حل مسائل استفاده کرد. به مثال بعدی توجه کنید.

مثال 12: طول یک مستطیل برابر با \(\Large 2x+6\) و عرض آن برابر با \(\Large 3x-2\) است. اگر نسبت طول به عرض مستطیل برابر با \(\Large \frac{5}{2}\) باشد، مساحت مستطیل را به دست آورید.

حل: نسبت طول به عرض مستطیل برابر با \(\Large \frac{5}{2}\) است. بنابراین داریم:

\(\LARGE \frac{2x+6}{3x-2}=\frac{5}{2}\)

چون دو کسر مساوی هستند، اگر آن‌ها را از یکدیگر کم کنیم باید برابر با صفر شوند. یعنی داریم:

\(\LARGE \frac{2x+6}{3x-2}-\frac{5}{2}=0\)

کافی است مخرج مشترک گرفته و صورت کسر را برابر با صفر قرار دهیم:

\(\LARGE \frac{2x+6}{3x-2}-\frac{5}{2}=0\)

\(\LARGE \Rightarrow \frac{2(2x+6)-5(3x-2)}{2(3x-2)}=0\)

\(\LARGE \Rightarrow \frac{4x+12-15x+10}{2(3x-2)}=0\)

\(\LARGE \Rightarrow \frac{-11x+22}{2(3x-2)}=0\)

\(\LARGE \Rightarrow -11x+22=0\)

\(\LARGE \Rightarrow x=2\)

بنابراین طول مستطیل که \(\Large 2x+6\) بود، برابر است با \(\Large 10\). عرض مستطیل که برابر با \(\Large 3x-2\) بود، برابر است با \(\Large 4\). در نتیجه، مساحت مستطیل برابر است با \(\Large 40\).

زنگ آخر کلاس  محاسبات عبارت های گویا نهم

در درسنامه‌ای که از ریاضی نهم خواندیم، ضرب و تقسیم و جمع و تفریق عبارات گویا را بررسی کردیم. همان طور که دیدید، برای به دست آوردن مخرج مشترک دو عبارت گویا، نیاز به محاسبهٔ ک.م.م آن‌ها بود. به همین خاطر، روش به دست آوردن ک.م.م عبارات جبری را نیز نشان دادیم. در انتهای درسنامه نیز، به محاسبهٔ عبارات مرکب و همچنین حل مسئله از عبارات گویا پرداختیم.

ما در ریاضیکا آماده‌ی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با محاسبات عبارت های گویا نهم دارید، در دیدگاه‌ها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند ‌داد.  

---

---