محاسبات ذهنی
محاسبه سریع جذر اعداد با فرجه دلخواه ✨☄️ – تند و تیز!
در این پست محاسبه سریع جذر اعداد را میتوانید فقط با یک حرکت پیدا کنید.
فرمول محاسبه سریع جذر اعداد
فرمول زیر را به خاطر بسپارید و با استفاده از آن جذر همه اعداد را حساب کنبد:
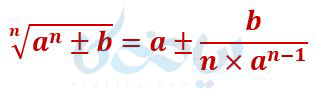
مثال ۱:
\(\LARGE \sqrt[3] {31} \)
حل ۱:
\(\LARGE \sqrt[3] {3^3+4}=3+\frac{4}{3\times 3^2} \)
\(\LARGE \frac{85}{27}=3.14 \)
مثال ۲:
\(\LARGE \sqrt[7] {125} \)
حل ۲:
\(\LARGE \sqrt[7] {2^7-3}=2-\frac{3}{7\times 2^6} \)
\(\LARGE \frac{893}{448}=1.99 \)
مثال ۳:
\(\LARGE \sqrt[3] {66} \)
حل ۳:
\(\LARGE \sqrt[3] {4^3+2}=4+\frac{2}{3\times 4^2} \)
\(\LARGE \frac{97}{24}=4.04 \)
مثال ۴:
\(\LARGE \sqrt[9] {538} \)
حل ۴:
\(\LARGE \sqrt[9] {2^9+26}=2+\frac{26}{9\times 2^8} \)
\(\LARGE \frac{2317}{1152}=2.01 \)
مثال ۵:
\(\LARGE \sqrt[2] {8} \)
حل ۵:
\(\LARGE \sqrt[2] {3^2-1}=3-\frac{1}{2\times 3^1} \)
\(\LARGE \frac{17}{6}=2.83 \)
توجه: هرچه اعداد بزرگتر باشد خطای این روش کمتر خواهد بود.
زنگ آخر
در این درسنامهای که از محاسبات ذهنی خواندیم، روش بسیار سادهای از این محاسبه سریع جذر اعداد را یادگرفتیم. با این فرمول میتوانید تمامی جذرها را چشمی حل کنید. و به راحتی آب خوردن به جواب همه جذرها میرسیم. هر سوالی از این مبحث داشتید در قسمت دیدگاه از ما بپرسید، کارشناسان ریاضیکا در اولین فرصت به سوالاتتان جواب میدهند.





با سلام و خسته نباشی.بسیاااار نکته ی مفید و عالی بود استاد.من ترم یک دانشگاه هستم و این نکته را به تازگی متوجه شدم و بسیار مشتاق هستم اثبات این راه حل را متوجه شوم.میتوانم از شما خواهش کنم که اثبات این راه حل را برایم بفرستید.ممنونم.
اثبات نکته ی ریشه ی اعداد با فرجه دلخواه
ممنونم??
روش بنای اریان حیدری😂😂عجب
دقیقا
دوست عزیز روش بنا برای آقای آریان حیدری نیست برای استاد منتطری هست که من ویدویوهاشو کامل دیدم تو بخش حد اینو کاملا گفتن و اثبات این قضیه با حد هست پس لطفا فکر نکنید این روش آریان حیدری هست
چه جالب
ببخشید، مقدار a و b چطوری بدست میاد؟
ببخشید، مقدار a و b چطور محاسبه میشه؟
با سلام وادب
مثلا اگه ریشه دوم ۳۴ رو میخواهیم محاسبه کنیم نزدیکترین عدد مجذور کامل به آن ۳۶ است این همان a است اختلاف ۳۶و۳۴ دوتا میشود که این همان b است
سلام، برای اعدادی مثل 35 جواب نمیده جذر 35 میشه 5.916
تو فرمول شما برای 35 باید a=5 , b=10 و n=2 باشه که در نهایت جواب درستی نمیده
کلا برای اعدادی که یک واحد تا مربع کامل فاصله دارن جواب با این فرمول اشتباه میشه ، مثلا برای 80 هم جواب اشتباه در میاد
باسلام
دوست عزیز برای همه اعداد جواب میده
الان نگاه کردم به منفی توجه نکرده بودم برای 35 باید a=6 ، b=1 و n=2 باشه در اینصورت همون 5.916 بدست میاد ، پس درسته
با سلام دوست عزیز
ممنون از بذل توجه شما بله گاهی باید جمع وگاهی کم کرد
دوست عزيز اگه به محاسبات سریع علاقمند هستید حتما دوره محاسبات سریع ما رو که به زودی آپدیت میشه رو تهیه کنید
سلام ریشه ۵ عدد ۷۲ با این فرمول نزدیک در نمیاد
سلام دوست عزیز از ۸۱استفاده کنید میشه آخر نه منهای نیم میشه هشت ونیم که فقط،دو صدم خطا داره
ردیکال سوم عدد 286را محاسبه نمائید
مرسیییی خیلی خوبه توضیحاتتون
ممنون
ببخشید میشه تمام رادیکال های فرجه 3 و4 و 5 رو خیلی کاربرد دارند بگید