احتمال یا اندازه گیری شانس ریاضی هفتم 💎💡 – روش محاسبه احتمال!

در درسنامهٔ احتمال یا اندازه گیری شانس ریاضی هفتم با یکدیگر می‌بینیم که چگونه می‌توان احتمال رخ دادن یک اتفاق را به صورت ریاضی محاسبه کرد. همچنین ارتباط احتمال ریاضی با آنچه را که در زندگی تجربه می‌کنیم، بررسی می‌کنیم. سعی می‌کنیم با حل مثال‌های مختلف، به درک بهتر شما از مبحث کمک کنیم. با ما تا انتهای درسنامه همراه باشید.

احتمال رخ دادن یک اتفاق

احتمال رخ دادن یک اتفاق برابر است با تعداد حالات مطلوب تقسیم بر تعداد حالات ممکن.

برای اینکه بهتر متوجه شوید، فرض کنید می‌خواهیم احتمال اینکه یک تاس زوج بیاید را محاسبه کنیم. حالت مطلوب این است که یکی از اعداد \(\Large 2\) یا \(\Large 4\) یا \(\Large 6\) بیاید؛ زیرا همگی زوج هستند. بنابراین تعداد حالات مطلوب برابر است با \(\Large 3\). از طرفی حالات ممکن، یکی از اعداد \(\Large 1\) تا \(\Large 6\) است. بنابراین، تعداد حالات ممکن برابر است با \(\Large 6\). در نتیجه، احتمال اینکه عددی زوج بیاید، برابر است با \(\Large \frac{3}{6}\). 

مثال از درسنامهٔ احتمال یا اندازه گیری شانس ریاضی هفتم

مثال 1 از احتمال یا اندازه گیری شانس ریاضی هفتم: سکه‌ای را پرتاب می‌کنیم. احتمال اینکه سکه پشت بیاید، چه قدر است؟

حل: حالت مطلوب برای ما این است که سکه پشت بیاید. بنابراین تعداد حالات مطلوب برابر است با \(\Large 1\). از طرفی حالات ممکن، یا رو آمدن سکه است و یا پشت آمدن آن. بنابراین، تعداد حالات ممکن برابر است با \(\Large 2\). پس، احتمال پشت آمدن سکه برابر است با تعداد حالات مطلوب تقسیم بر تعداد حالات ممکن؛ یعنی برابر است با \(\Large \frac{1}{2}\).

مثال از درسنامهٔ احتمال یا اندازه گیری شانس ریاضی هفتم

مثال 2 از احتمال یا اندازه گیری شانس ریاضی هفتم: جعبه‌ای شامل \(\Large 3\) مهرهٔ آبی و \(\Large 4\) مهرهٔ قرمز است. اگر بدون نگاه کردن، یک مهره از جعبه خارج کنیم، احتمال اینکه مهرهٔ بیرون آمده آبی باشد چه قدر است؟ احتمال اینکه مهره‌ای سبزرنگ بیرون بیاید چه قدر است؟

حل: ابتدا احتمال بیرون آمدن مهرهٔ آبی را مقایسه می‌کنیم. حالات مطلوب ما این است که یکی از \(\Large 3\) مهرهٔ آبی ‌رنگ داخل جعبه بیرون بیاید. بنابراین، تعداد حالات مطلوب برابر است با \(\Large 3\). از طرفی، حالات ممکن، بیرون آمدن یکی از \(\Large 7\) مهرهٔ داخل جعبه است. بنابراین، تعداد حالات ممکن برابر است با \(\Large 7\). در نتیجه، احتمال بیرون آمدن مهره‌ای آبی رنگ برابر است با \(\Large \frac{3}{7}\).

اما بیایید احتمال بیرون آمدن مهره‌ای سبز رنگ را محاسبه کنیم. هیچ یک از حالات بیرون آمدن مهره، مطلوب ما نیست؛ زیرا در هر صورت، مهره‌ای سبز رنگ از جعبه بیرون نخواهد آمد. پس تعداد حالات مطلوب برابر است با \(\Large 0\). حالات ممکن نیز، بیرون آمدن یکی از \(\Large 7\) مهره از جعبه است. بنابراین، احتمال بیرون آمدن مهرهٔ سبز برابر است با تعداد حالات مطلوب تقسیم بر تعداد حالات ممکن، که این مقدار برابر با \(\Large \frac{0}{7}\) یا همان \(\Large 0\) است.

مثال از درسنامهٔ احتمال یا اندازه گیری شانس ریاضی هفتم

مثال 3 از احتمال یا اندازه گیری شانس ریاضی هفتم: دو جعبه داریم. در جعبهٔ اول \(\Large 3\) مهرهٔ سبز و \(\Large 5\) مهرهٔ زرد و در جعبهٔ دوم \(\Large 4\) مهرهٔ سبز و \(\Large 7\) مهرهٔ زرد وجود دارد. اگر از هر جعبه یک مهره برداریم، احتمال بیرون آمدن مهرهٔ سبزرنگ از کدام جعبه بیشتر است؟

حل: ابتدا احتمال بیرون آمدن مهرهٔ سبز رنگ از جعبهٔ اول را محاسبه می‌کنیم. حالات مطلوب ما در جعبهٔ اول، بیرون آمدن یکی از \(\Large 3\) مهرهٔ سبزرنگ است. بنابراین تعداد حالات مطلوب در جعبهٔ اول برابر با \(\Large 3\) است. حالات ممکن نیز، بیرون آمدن یکی از \(\Large 8\) مهرهٔ موجود در جعبهٔ اول است. بنابراین، احتمال بیرون آمدن مهرهٔ سبزرنگ از جعبهٔ اول برابر است با \(\Large \frac{3}{8}\).

در مورد جعبهٔ دوم، حالات مطلوب ما بیرون آمدن یکی از \(\Large 4\) مهرهٔ سبزرنگ است. بنابراین تعداد حالات مطلوب در جعبهٔ دوم برابر با \(\Large 4\) است. حالات ممکن نیز، بیرون آمدن یکی از \(\Large 11\) مهرهٔ موجود در جعبهٔ دوم است. بنابراین، احتمال بیرون آمدن مهرهٔ سبزرنگ از جعبهٔ دوم برابر است با \(\Large \frac{4}{11}\).

حال باید دو عدد \(\Large \frac{3}{8}\) و \(\Large \frac{4}{11}\) را با یکدیگر مقایسه کنیم. برای این‌کار مخرج مشترک می‌گیریم. مخرج مشترک دو کسر \(\Large \frac{3}{8}\) و \(\Large \frac{4}{11}\) برابر با \(\Large 88\) است. پس داریم:

\(\LARGE \frac{3}{8}=\frac{33}{88}\)

\(\LARGE \frac{4}{11}=\frac{32}{88}\)

در نتیجه، احتمال اینکه مهرهٔ خارج شده از جعبهٔ اول سبز رنگ باشد، بیشتر است.

مثال از درسنامهٔ احتمال یا اندازه گیری شانس ریاضی هفتم

مثال 4 از احتمال یا اندازه گیری شانس ریاضی هفتم: تیری به سمت یک هدف به شکل زیر پرتاب می‌کنیم. احتمال اینکه تیر به یکی از قسمت‌های سبز رنگ برخورد کند چه قدر است؟

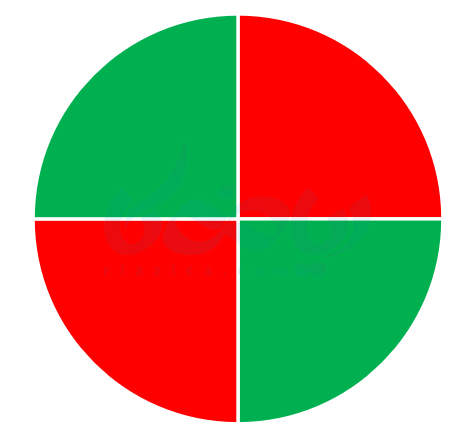
حل: همان طور که می‌بینید، دایره به چهار ربع دایره تقسیم شده است. حالات مطلوب ما، برخورد تیر به یکی از دو ربع دایرهٔ سبز رنگ است. بنابراین، تعداد حالات مطلوب برابر با \(\Large 2\) است. حالات ممکن نیز، برخورد تیر به یکی از چهار ربع دایره است. بنابراین تعداد حالات ممکن برابر با \(\Large 4\) است. در نتیجه، احتمال اینکه تیر به یکی از قسمت‌های سبز رنگ بخورد، برابر است با \(\Large \frac{2}{4}\).

احتمال و تجربه ریاضی هفتم

وقتی می‌گوییم اگر یک سکه را پرتاب کنیم، احتمال اینکه پشت بیاید برابر با \(\Large \frac{1}{2}\) است، آیا با دو بار پرتاب سکه، لزوماً یک بار پشت و بار دیگر رو خواهد آمد؟ یا مثلاً احتمال اینکه تاس شش بیاید، برابر با \(\Large \frac{1}{6}\) است. آیا اگر تاس را شش بار پرتاب کنیم، حتما یکبار \(\Large 6\) خواهد آمد؟ یا مثلاً اگر احتمال رخ دادن یک اتفاق برابر با \(\Large \frac{1}{3}\) باشد، آیا لزوماً در \(\Large \frac{1}{3}\) آزمایش‌ها آن اتفاق رخ خواهد داد؟

پاسخ منفی است. درست نیست که در ریاضیات از تجربه صحبت کنیم؛ اما اگر مواردی که گفتیم را تجربه هم کنیم، به پاسخ منفی می‌رسیم. وقتی می‌گوییم احتمال رخ دادن یک اتفاق برابر با \(\Large \frac{1}{5}\) است، یعنی اگر تعداد آزمایش‌ها به بی‌نهایت میل کند، در \(\Large \frac{1}{5}\) موارد، اتفاق مطلوب رخ خواهد داد. از آنجاییکه بی‌نهایت آزمایش یک پدیده در عمل برای ما ممکن نیست، طبیعی است که با تعداد محدودی آزمایش، به نتیجهٔ مورد نظر نمی‌رسیم.

برای علاقه‌مندان: در صورتی که علاقه‌مندید، در مورد قانون اعداد بزرگ مطالعه کنید.

برای یادگیری مطالب بیشتر در مورد احتمال به پست آموزش احتمال هشتم مراجعه کنید

زنگ آخر کلاس احتمال یا اندازه گیری شانس ریاضی هفتم

در درسنامه‌ای که از ریاضی هفتم خواندیم، ابتدا روش محاسبهٔ احتمال رخ دادن یک اتفاق را بررسی کردیم. با استفاده از آنچه که آموختیم، در مثال‌های مختلف، احتمال رخدادن پیشامدهای مختلف را به دست آوردیم. در انتهای درسنامه نیز، به بررسی ارتباط بین احتمال ریاضی و آنچه که در زندگی تجریه می‌کنیم پرداختیم.

ما در ریاضیکا آماده‌ی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با احتمال یا اندازه گیری شانس ریاضی هفتم دارید، در دیدگاه‌ها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند ‌داد.