آموزش ریاضی پایه یازدهم تجربی
آموزش تابع لگاریتمی – تابع معکوس موفقیت🔄〽️
تابع لگاریتمی و آموزش تابع لگاریتمی بخش مهمی از دنیای ریاضی را تشکیل میدهند. در ریاضیات و در علوم مختلف مانند شیمی و فیزیک و نجوم گاهی با طیف وسیعی از اعداد برخورد میکنیم. عددهای خیلی بزرگ یا خیلی کوچک که برای سادگی در نوشتن و محاسبات، می توان آنها را توانهایی از یک عدد خاص در نظر گرفت. یعنی میتوانیم اعداد خیلی بزرگ را با ابعاد بسیار کوچکتری نشان دهیم. یا برعکس، عددهای بسیار کوچک را به صورت مناسب نمایش داد.
این جا است که سر و کلهٔ توابع نمایی و لگاریتمی و کاربردهای آنها پیدا میشود. روش لگاریتمگیری در سال ۱۶۱۴ توسط جان نپر ریاضیدان اسکاتلندی در کتابی به عنوان توصیفی بر کانون شگفت انگیز لگاریتم مطرح شد.
ما در این درسنامه به روشی کاملا جدید ومفهومی رسم نمودار تابع لگاریتم را بیان کردیم که خواندن آن خالی از لطف نیست.
آموزش تابع لگاریتمی: چند مثال برای فهم بیشتر
بیاید برای درک بهتر از لگاریتم، ابتدا با چند مثال این مفهوم و رابطهٔ تابع نمایی و تابع لگاریتمی را بیان کنیم.
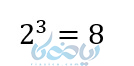
اگر من از شما بپرسم ۲ به توان چه عددی برسد میشود ۸، شما پاسخ می دهید ۳. این مفهوم را با نماد لگاریتم و به صورت زیر مینویسند.
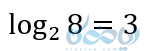
برای خواندن عبارت بالا باید بگوییم:
لگاریتم 8 در مبنای 2 میشود 3
در نهایت عبارت زیر نتیجه میشود:
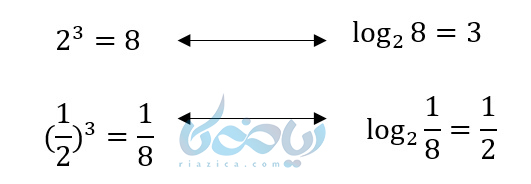

نکتهٔ مهم: مفهوم لگاریتم و توان هردو برعکس هم هستند و از یکی میتوانیم دیگری را نتیجه بگیریم.
تعریف تابع لگاریتمی:
در ادامهٔ آموزش تابع لگاریتمی میخواهیم یک مفهوم مهم را باهم بررسی کنیم. تابع نمایی یک تابع یک به یک و وارون پذیر است. به تابع زیر دقت کنید:
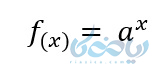
وارون تابع بالا برابر با عبارت زیر است:
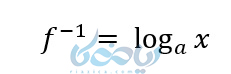
برای خواندن عبارت فوق میگوییم:
لگاریتم x در مبنای a
دامنهٔ توابع نمایی اعداد حقیقی هستند و برد آنها اعداد حقیقی مثبت میباشند. مبنا نیز عدد مثبت مخالف یک می باشد.
یک جمعبندی تا اینجای آموزش تابع لگاریتمی
در زیر تمام آنچه تا اینجا گفته شد را به صورت یکجا مشاهده میکنید.

نمودار توابع لگاریتمی:
در مبحث تابع نمایی مشاهده کردید که اگر در توابع نمایی \( \Large a > 1 \) باشد، تابع یک تابع صعودی است. نمودار آن به صورت زیر نمایش میدهیم:
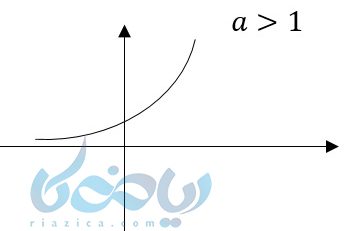
این تابع یک به یک است و وارون پذیر. همانطور که در بخش تابع بیان کردیم، برای رسم تابع وارون، قرینه آن را نسبت به نیمساز ربع اول و سوم رسم میکنیم. به مثال زیر دقت کنید.
\( \LARGE y = 2^x \)
| 1 | \( \Large 0 \) | -1 | x |
|---|---|---|---|
| 2 | 1 | \( \Large \frac{1}{2} \) | y |
اگر جدول را وارون کنیم داریم:
\( \LARGE y =log_2 x \)
| 2 | 1 | \( \Large \frac{1}{2} \) | x |
|---|---|---|---|
| 1 | \( \Large 0 \) | -1 | y |
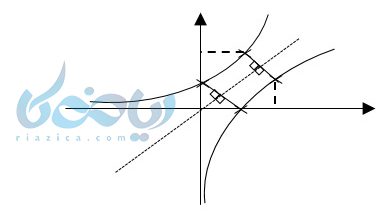
از جدول و نمودار بالا نتایج زیر بدست میآیند:
\( \LARGE y =log_2 2 = 1 \)
\( \LARGE y =log_2 1 = 0 \)
\( \LARGE y =log_2 {\frac{1}{2}} = -1 \)
همانطور که می بینید نمودار \( \Large y = log_2 x \) که در آن مبنا بزرگتر از یک است صعودی میباشد. این نمودار محور yها را قطع نمیکند و در کنار آن به سمت منفی بینهایت میرود. همچنین محور xها را در نقطه 1 قطع میکند. در این نمودار محور yها یک مجانب عمودی میباشد که نمودار در کنار آن به سمت بینهایت میرود.
بهتر بفهمید: یک مثال دیگر از آموزش تابع لگاریتمی
مثال زیر دقت کنید:
\( \LARGE y = (\frac{1}{2})^x \)
| 1 | \( \Large 0 \) | -1 | x |
|---|---|---|---|
| \( \Large \frac{1}{2} \) | 1 | 2 | y |
پس جدول آن به صورت زیر است:
\( \LARGE y = log_{\frac{1}{2}} x \)
| \( \Large \frac{1}{2} \) | 1 | 2 | x |
|---|---|---|---|
| 1 | \( \Large 0 \) | -1 | y |
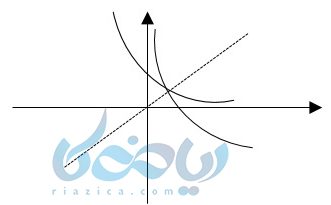
از این نمودار متوجه میشویم:
\( \LARGE y =log_{\frac{1}{2}} {2} = -1 \)
\( \LARGE y =log_{\frac{1}{2}} 1 = 0 \)
\( \LARGE y =log_{\frac{1}{2}} {\frac{1}{2}} = 1 \)
در این تابع لگاریتمی که \( \Large 0 < a < 1 \) است تابع نزولی است. باز تابع محور yها را قطع نمی کند و در کنار آن به سمت مثبت بینهایت میرود. همچنین این نمودار محور xها را در نقطه 1 قطع میکند.
با توجه به نمودارهای رسم شده و آنچه که تا اینجا در مبحث آموزش تابع لگاریتمی یادگرفتهایم، به 3 ویژگی مهم لگاریتم پی میبریم:
- لگاریتم هر عدد در مبنای خودش مساوی یک میشود.
- لگاریتم یک در هر مبنایی صفر میشود.
- اگر شناسه لگاریتم و مبنا معکوس هم باشند مقدار منفی یک میشود.
در زیر سه ویژگی بالا را به صورت فرمول نیز میتوانید مشاهده کنید.
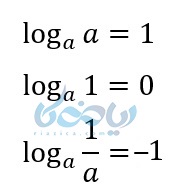
رسم توابع لگاریتمی
1- رسم نمودار تابع لگاریتمی \( \LARGE y =log_a x \) به روش ساده و دقیق
نقطهیابی
برای رسم توابع لگاریتمی ساده مانند \( \Large y =log_a x \) مانند \( \Large y =log_{\frac{1}{2}} x \) از روش نقطهیابی استفاده میکنیم، ابتدا سه مقدار برای طول در نظر میگیریم:
- مبنا
- یک
- معکوس مبنا
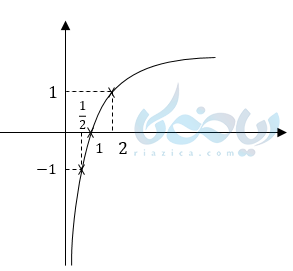
مثلا در مورد تابع \( \Large y =log_2 x \) و \( \Large y =log_{\frac{1}{2}} x \) سه عدد \( \Large 1 , 2 , \frac{1}{2} \) را به جای \( \Large x \) قرار میدهیم ، طبق سه قانونی که در بالا ذکر کردیم خواهیم داشت:
\( \LARGE y =log_2 x \)
| 2 | 1 | \( \Large \frac{1}{2} \) | x |
|---|---|---|---|
| 1 | \( \Large 0 \) | -1 | y |
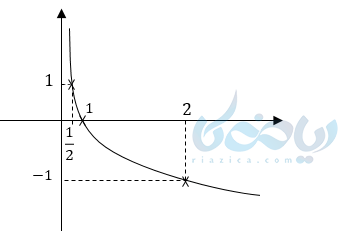
\( \LARGE y =log_{\frac{1}{2}} x \)
| 2 | 1 | \( \Large \frac{1}{2} \) | x |
|---|---|---|---|
| -1 | \( \Large 0 \) | 1 | y |
و بعد در محور مختصات به راحتی این سه نقطه را پیدا کرده و نمودار را رسم میکنیم.
دقت داشته باشید که چون دامنه هر دو تابع اعداد حقیقی مثبت میباشد پس نمودار از محور \( \Large x \)ها عبور نمیکند و در کنار آن به سمت بینهایت میرود به اصطلاح محور \( \Large y \)ها در اینجا خط مجانب است.
\( \LARGE y =log_2 x \)
\( \LARGE y =log_{\frac{1}{2}} x \)
2-رسم توابع لگاریتمی \( \LARGE y =log_a {(x\pm b)} \)
اما برای رسم نمودار توابعی که به صورت \( \Large y =log_a {(x\pm b)} \) هستند. \( \Large (a>0) \)
الف) روش انتقال
اگر بخواهیم به روش انتقال عمل میکنیم ابتدا نمودار تابع ساده آن یعنی \( \Large y =log_a x \) را به روش که در بالا گفتیم رسم میکنیم سپس اگر \( \Large x + b \) داشتیم نمودار را به اندازه \( \Large b \) به سمت چپ منتقل میکنیم و اگر \( \Large x – b \) بود نمودار را به اندازه \( \Large b \) به سمت راست منتقل میکنیم.
به اصطلاح میگوییم تابع در این مواقع لجباز است وعمل روی آن یک عمل درونی است یعنی یک عمل روی \( \Large x \) اعمال شده و خط مجانب در این مواقع خط \( \Large x = -b \) خواهد بود.
مثلا در مورد \( \Large y =log_2 {(x – 1)} \) داریم:

ب) روش نقطه یابی
اگر بخواهیم دقیقتر نمودار را رسم میکنیم ابتدا جدول تابع ساده را مینویسیم یعنی
\( \Large y =log_a x \) سپس در این جدول به طولها به اندازه \( \Large -b \) اضافه میکنیم یا به اصطلاح اگر \( \Large x \) با \( \Large b \) جمع شده باشد ما طولها را منهای \( \Large b \) و اگر کم شده باشد طولها را بعلاوه میکنیم در مثال \( \Large y =log_2 {(x – 1)} \) داریم:
\( \LARGE y =log_2 x \)
| 2 | 1 | \( \Large \frac{1}{2} \) | x |
|---|---|---|---|
| 1 | \( \Large 0 \) | -1 | y |
طولها را بعلاوه یک میکنیم:
| 3 | 2 | \( \Large 1\frac{1}{2} \) | x |
|---|---|---|---|
| 1 | \( \Large 0 \) | -1 | y |
همانطور که گفتیم خط مجانب \( \Large x=-b \) است بهتر آن است که ابتدا خط مجانب را مشخص کنیم سپس نمودار را رسم کنیم.

نکته: کشیدن خط مجانب بدان خاطر است که دقت کنیم نمودار از این خط عبور نکند و به موازات آن به سمت بینهایت برود چون دامنه در این تابع \( \Large x > 1 \) میباشد.
3-رسم توابع لگاریتمی \( \LARGE y =log_a {x \pm c} \)
الف) روش انتقال
برای رسم توابع لگاریتمی به روش انتقال که به صورت \( \Large y =log_a {x \pm c} \) میباشند ابتدا نمودار تابع ساده آن \( \Large y =log_a x \) را رسم میکنیم سپس آن را به سمت بالا یا پایین منتقل میکنیم به اصطلاح انتقال عمودی است بدین صورت که اگر بعلاوه \( \Large c \) باشد انتقال به سمت بالا و اگر منها \( \Large c \) باشد انتقال به سمت پایین خواهد بود و تابع از علامت \( \Large c \) تبعیت میکند.
مثال: نمودار تابع \( \Large y =log_2 {x + 1} \) را رسم کنید؟
حل: ابتدا نمودار تابع \( \Large y =log_2 {x} \) را رسم کرده سپس یک واحد به سمت بالا منتقل میکنیم.
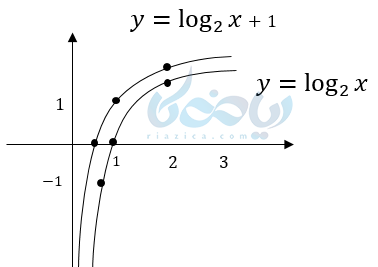
نکته: دقت کنید خط مجانب هر دو محور \( \Large y \)ها یا همان خط \( \Large x = 0 \) است چون دامنه تغییری نکرده است.
ب) روش نقطهیابی
در این روش ابتدا جدول مربوط به تابع یعنی \( \Large y =log_a {x} \) را مینویسیم سپس اگر بعلاوه \( \Large c \) شده باشد عرضها را با \( \Large c \) جمع و اگر منها \( \Large c \) شده باشد عرضها را منهای \( \Large c \) کرده و جدول جدید را رسم میکنیم.
در مثال بالا خواهیم داشت:
\( \LARGE y =log_2 x \)
| 2 | 1 | \( \Large \frac{1}{2} \) | x |
|---|---|---|---|
| 1 | \( \Large 0 \) | -1 | y |
عرضها را بعلاوه یک میکنیم:
| 2 | 1 | \( \Large \frac{1}{2} \) | x |
|---|---|---|---|
| 2 | 1 | \( \Large 0 \) | y |
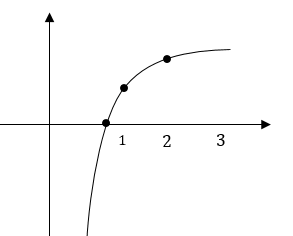
4-رسم نمودار توابعی لگاریتمی که به صورت \( \LARGE y =log_a {(x \pm b)} \pm c \)
الف)انتقال
انتقال این توابع هم انتقال افقی دارند هم عمودی باز ابتدا نمودار تابع ساده آنها را رسم میکنیم و بعد به اندازه \( \Large c , b \) آن را به ترتیب به سمت (چپ یا راست) و (بالا و پایین) منتقل میکنیم.
مثال: \( \Large y =log_2 {(x + 2)} – 2 \) را رسم کنید؟
ابتدا نمودار \( \Large y =log_2 {x } \) را رسم میکنیم و بعد دو واحد به چپ و دو واحد به پایین منتقل میکنیم، خط مجانب \( \Large x = -2 \)
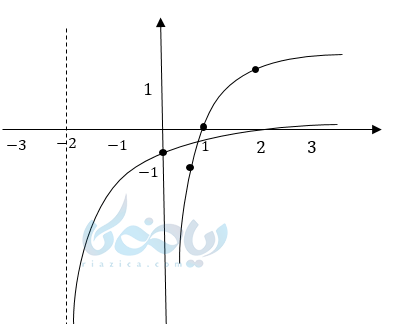
ب) روش نقطه یابی
در این روش ابتدا جدول مربوط به تابع ساده را مینویسیم، یعنی \( \Large y =log_2 x \) سپس طول نقاط با قرینه b و عرض نقاط را با خود c جمع میکنیم و جدول جدید را رسم مینماییم:
مثال: \( \Large y =log_2 {(x+2)} – 2 \) را رسم کنید؟
\( \LARGE y =log_2 x \)
| 2 | 1 | \( \Large \frac{1}{2} \) | x |
|---|---|---|---|
| 1 | \( \Large 0 \) | -1 | y |
طولها منهای 2 و عرضها منهای 2:
| \( \Large 0 \) | -1 | \( -1\Large \frac{1}{2} \) | x |
|---|---|---|---|
| -1 | -2 | -3 | y |
خط مجانب \( \Large x = -b \)
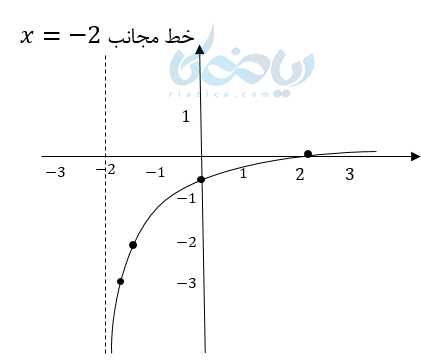
قرینه تابع لگاریتمی
\( \LARGE y = log_2 x , (x>0) \)
| 2 | 1 | \( \Large \frac{1}{2} \) | x |
|---|---|---|---|
| 1 | \( \Large 0 \) | -1 | y |
\( \LARGE y = log_2 {-x} , (x<0) \)
| -2 | -1 | –\( \Large \frac{1}{2} \) | x |
|---|---|---|---|
| 1 | \( \Large 0 \) | -1 | y |
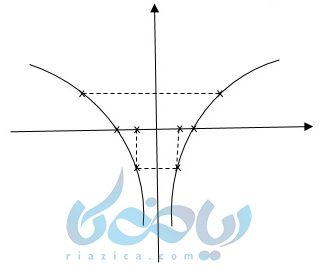
همانطور که میبینید وقتی \( \Large x \) قرینه میشود و نمودار تابع نسبت به محور \( \Large y \) ها قرینه میشود .
چون دامنه تابع \( \Large y = log_2 {(-x)} \) برابر با \( \Large (-\infty , 0) \) خواهد بود، ولی \( \Large y \) ها تغییر نمیکند. پس نمودار تابع نسبت به محور \( \Large y \) ها قرینه میشود.
در مورد \( \Large y = – log_2 {x} \) باید گفت که دامنه تغییر نمیکند. بلکه این \( \Large y \) ها هستند که قرینه میشوند. پس نمودار نسبت به محور \( \Large x \) ها قرینه میشود. درست برعکس تابع نمایی، پس طبق آموزشهایی که تا به اینجا از تابع لگاریتمی باهم یادگرفتیم خواهیم داشت:
\( \LARGE y = log_2 x (x>0) \)
| 2 | 1 | \( \Large \frac{1}{2} \) | x |
|---|---|---|---|
| 1 | \( \Large 0 \) | -1 | y |
\( \LARGE y = -log_2 x (x>0) \)
| 2 | 1 | \( \Large \frac{1}{2} \) | x |
|---|---|---|---|
| -1 | \( \Large 0 \) | 1 | y |
در ادامه حتما پست آموزش حل لگاریتم را مشاهده کنید.
زنگ آخر : آموزش تابع لگاریتمی
در درس توابع نمایی گفتیم که تابع نمایی تابع موفقیت است. به یاد داشته باشید که اگر تلاش شما پیوسته باشد موفقیتهای شما مثل تابع نمایی رشد خواهند کرد. اما عکس این مطلب نیز صادق است. یعنی اگر تلاش کافی نداشته باشیم، شکستهای ما با هم جمع خواهند شد و در نهایت مثل معکوس تابع نمایی که لگاریتمی است، با شیب تند به سمت شکستهایمان پیش میرویم.
ما در ریاضیکا آمادهایم تا به شما براي موفقیت در تحصیل و زندگی کمک کنیم. اگر هر سوالی در مورد مبحث آموزش تابع لگاریتمی دارید، سوال خود را در قسمت دیدگاهها بپرسید. کارشناسان ما به شما پاسخ خواهند داد.





عالی بود واقعا
با سلام
ممنون از نظر شما
خیلی خیلی عالی
با سلام وادب
ممنون از لطف شما
بسیار عالی
عالی بود خدا قوت
با سلام
ممنون از دیدگاه مثبت شما
بسیار عالی
بسیار عالی
درجه یک
با سلام ممنون از نظر شما
عالیییییییییی بود
سلام ممنون از نظر،شما
تو مثالا یه غلط دارید درستش کنید
لگاریتم یک هشتم در مبنای 2 میشه منفی سه
نه یک دوم
چشم تصحیح میشه