آموزش ریاضی پایه یازدهم تجربی
وارون تابع ریاضی یازدهم تجربی 🚗☯️ – برعکسش کن!
در مبحث تابع بعضی از توابع مکمل و کامل کننده هم هستند و بدون یکدیگر تعریف نمیشوند و با یکدیگر روابط و نمودارهای زیبایی میسازند برای درک این مفهوم باید وارون تابع را بشناسیم و به درک بهتری از توابع برسیم. ما در این مبحث مفهوم وارون تابع ریاضی یازدهم تجربی را به طور کامل و شفاف همراه با نمودار برای شما بیان کردیم.
مفهوم وارون تابع ریاضی یازدهم تجربی
اگر در یک تابع یک به یک جای \( \Large x \) و \( \Large y \) یا همان مولفههای اول و دوم را با هم جابجا کنیم تابع جدید بدست آمده را وارون تابع اول را مینامند و آن را با \( \Large f^{-1} \) نمایش میدهند. به وارون یک تابع، معکوس تابع نیز گفته میشود. وقتی وارون یک تابع را مینویسیم در واقع جای دامنه و برد تابع جابجا میشود.
\( \LARGE f \rightarrow f^{-1} \)
\( \LARGE D_f \rightarrow R_{ f^{-1}}\)
\( \LARGE R_f \rightarrow D_{ f^{-1}}\)
مثال ۱ از تابع وارون: وارون تابع زیر را بنویسید.
\( \LARGE f =\{(1,3),(4,-2),(5,7)\} \)
جواب ۱:
\( \LARGE f^{-1} =\{(3,1),(-2,4),(7,5)\} \)
میدانیم قرینه محوری نقطه \( \Large (a,b) \) نسبت به نیمساز ربع اول و سوم (خط \( \Large y=x \)) که نقطه \( \Large (b,a) \) میشود.
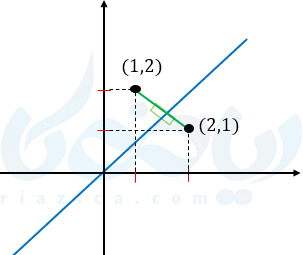
از این خاصیت برای رسم نمودار وارون یک تابع استفاده کنیم بدین صورت که وقتی نمودار وارون یک تابع را از ما خواستند قرینه محوری آن را نسبت به نیمساز ربع اول و سوم یعنی خط \( \Large y=x \) بدست میآوریم. جالب است بدانید اگر نقطه ای در ربع اول یا سوم باشد وارون آن نیر در ربع اول یا سوم است اما اگر نقطه ای در ربع دوم باشد وارون آن در ربع چهارم واگر در ربع چهارم باشد وارون آن در ربع دوم خواهد بود.
مثال ۲ از وارون تابع: نمودار وارون تابع زیر را رسم کنید.
جواب ۲:
نیمساز ربع اول و سوم را رسم کرده سپس سه نقطه از نمودار را در نظر گرفته و قرینه محوری آنها را نسبت به خط \( \Large y=x \) پیدا کرده و نقاط را به هم وصل میکنیم. در نتیجه معکوس تابع را بدست میآوریم.
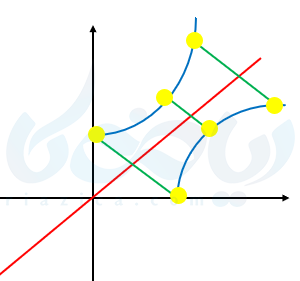
نکته مهم وارون تابع ریاضی یازدهم تجربی: البته شرط وارون پذیری یک تابع یک به یک بودن آن است. اگر تابع یک به یک نباشد وارون پذیر نیست چون وارون آن دیگر تابع نیست مگر آنکه بتوان با محدود کردن دامنه ابتدا آن را یک به یک کنیم سپس وارون تابع آن را بدست آوریم.
مثال ۳ از تابع معکوس: وارون توابع زیر را بدست آورید.
الف)
ب)
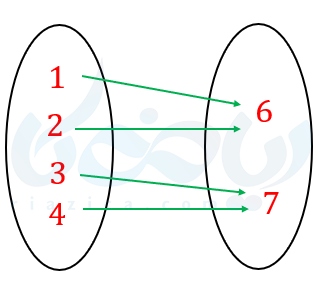
جواب ۳:
الف) یک به یک است پس وارون پذیر است.
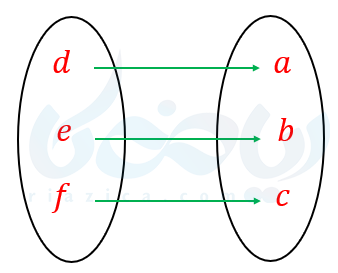
ب)
یک به یک نیست پس وارون پذیر نیست.
ضابطه تابع وارون یک تابع خطی غیر ثابت
میداینم تمام توابع خطی به غیر از توابع ثابت (\( \Large y=b \)) یک به یک و وارون پذیر هستند و وارون آنها نیز یک خط است.
برای بدست آوردن ضابطه تابع وارون یک خط از روی ضابطه آن ابتدا در معادله یا همان ضابطه خط جای \( \Large x \) و \( \Large y \) را عوض کرده سپس معادله را بر حسب \( \Large y \) مرتب میکنیم.البته می توانیم ابتدا تابع را بر حسب \( \Large x\) مرتب کنیم سپس جای \( \Large x \) و \( \Large y \) را عوض کنیم.
مثال ۴ از معکوس تابع: وارون تابع \( \Large f(x)=2x+1 \) را بدست آورید.
جواب ۴:
\( \LARGE y=2x+1 \)
جای \( \Large x \) و \( \Large y \) عوض میشود.
\( \LARGE x=2y+1 \)
\( \Large y \) را انتها میکنیم.
\( \LARGE 2y=x-1 \rightarrow y=\frac{x-1}{2} \)
\( \LARGE f^{-1}=\frac{x-1}{2} \)
در تابع \( \Large f(x)=2x+1 \) اگر به تابع یک بدهیم به ما عدد ۳ را تحویل میدهد. حال اگر در تابع \( \Large f^{-1}=\frac{x-1}{2} \) عدد ۳ را جایگذاری میکنیم به ما عدد ۱ تحویل میدهد.
\( \LARGE f :(1,3) \)
\( \LARGE f^{-1} :(3,1) \)
مثال ۵ از تابع معکوس: وارون تابع \( \Large f(x)=\frac{2}{3}x-4 \) را بدست آورید.
جواب ۵:
\( \LARGE y=\frac{2}{3}x-4 \)
جای \( \Large x \) و \( \Large y \) عوض میشود.
\( \LARGE x=\frac{2}{3}y-4 \)
\( \Large y \) را انتها میکنیم.
\( \LARGE 3x=2y-12 \)
\( \LARGE 2y=3x+12 \)
\( \LARGE y=\frac{3}{2}x+6 \)
نکته وارون تابع ریاضی یازدهم تجربی: در مورد بقیه توابع غیرخطی نیز ابتدا یک به یک بودن آن را بررسی میکنیم سپس یه همین صورت یعنی با جابجایی \( \Large x \) و \( \Large y \) و تنها کردن \( \Large y \) ضابطه وارون تابع را بدست میآوریم.
مثال ۶ از معکوس تابع: آیا تابع \( \Large y=-x^3 + 2 \) ، یک به یک است؟ در صورت یک به یک بودن ضابطه تابع وارون آن را بنویسید.
جواب ۶:
ابتدا یک به یک بودن آن را بررسی میکنیم:
\( \LARGE f(x_1)=f(x_2) \)
\( \LARGE -x_1^3 + 2=-x_2^3 + 2 \)
\( \LARGE x_1^3 =x_2^3 \)
\( \LARGE x_1=x_2 \)
تابع یک به یک است.
ضابطه تابع وارون بدست میآوریم:
\( \LARGE y=-x^3 + 2 \)
جای \( \Large x \) و \( \Large y \) عوض میشود.
\( \LARGE x=-y^3 + 2 \)
\( \Large y \) را نتها میکنیم.
\( \LARGE y^3 =-x+ 2 \)
\( \LARGE y =\sqrt[3] {-x+2} \)
\( \LARGE f^{-1}(x) =\sqrt[3] {-x+2} \)
توصیه میشه برای یادگیری بیشتر این مطلب قبلش پست تابع یک به یک رو مطالعه کنیدودر ادامه پست تابع وارون رو هم بخوانید.
کلام آخر وارون تابع ریاضی یازدهم تجربی
در این نوشتار با آموزش وارون تابع ریاضی یازدهم تجربی آشنا شدید. نوشتن وارون تابع و ضابطه معکوس آن با تمرین و حل کردن تمارین به راحتی قابل امکان است.
دوستان ریاضیکا هر سوالی از تابع وارون و ریاضی یازدهم تجربی داشتید برایمان در قسمت دیدگاه بنویسید. کارشناسان ریاضیکا حتما به سوالاتتان پاسخ میدهند.





برای رسمنموداروارونیک تابع کافیستقرینه ی نمودارآن تابع رانسبت به خط……رسم کنیم
با سلام وعرض ادب
نیمساز ربع اول وسوم خط y=x
با سلام
کدام توابع وارون پذیر هستند؟ فقط توابع یک به یک؟
با سلام وادب
بله فقط توابع یک به یک وارون پذیر هستن
درچه حالتی تابع خطی با وارونش برابر است؟
با سلام وادب
فقط تابع خطیy=x یا همان تابع همانی
آیا وارون تابع “سه پنجم” برابر “پنج سوم” است؟
و چرا؟
با سلام تابع سه پنجم یه تابع ثابت هست پس وارون پذیر نیست
چجور بدون رسم نمودار وارون پذیری تابع رو بررسی کنیم ??
با سلام وادب به ایکس مقدار بدید اگه برای وای دو جواب بدیت بیاد وارون پذیر نیست البته به دامنه تابع هم باید توجه کرد
با سلام و تشکر
وارون تابع g(x)= 2f(3x-1)+1 چطور محاسبه میشود؟
ممنون
عالی
اگه + درسنامه فیلم آموزشی هم بزارید عالی میشه
سلام دوست عزیز برا خیلی از پستها گذاشتیم