ترسیم های هندسی – آموزش گام به گام📈 📷و عملی به زبان ساده

سلام به همهٔ شما اهالی ریاضیکا. در کتاب هندسه 2 از پایه یازدهم با آموزش ترسیم های هندسی به روش منطقی و استدلالی آشنا می‌شویم. به همین خاطر قصد داریم در این پست آموزشی این موضوع مهم را به طور کامل به شما آموزش دهیم. مواردی که در این بخش باهم یاد خواهیم گرفت عبارتند از:

• تعریف و ترسیم عمود منصف و نیمساز
• رسم دوخط موازی
• رسم خط عمود بر یک خط، از یک نقطه‌ٔ خارج یا واقع بر آن

تمام آموزش ترسیم های هندسی بر اساس استدلال استنتاجی و با استفاده از اثبات قضایایی که در این بخش بیان شده انجام می‌پذیرد.

عمود منصف و خواص آن با کمک ترسیم های هندسی

تعریف عمود منصف

می دانیم عمود منصف یک پاره خط ، خطی است که بر آن عمود شده و آن را نصف می‌کند. حال می‌خواهیم با استفاده از ترسیم های هندسی در مورد یک خاصیت مهم عمود منصف صحبت کنیم.

قضیه اساسی عمود منصف

هر نقطه که روی عمود منصف یک پاره خط واقع باشد از دو سر پاره خط به یک اندازه است وبالعکس

ما در اینجا این قضیه مهم عمود منصف وعکس آن را در قالب دو قضیه جدا برایتان اثبات نموده ایم:

قضیه 1: هر نقطه روی عمود منصف یک پاره خط از دو سر آن پاره خط به یک اندازه است. اما چرا؟

اثبات: پاره خط\( \Large AB \) و عمود منصف آن را در نظر بگیرید، و نقطه \( \Large M \) را روی عمود منصف پاره خط \( \Large AB \)  فرض کنید. از \( \Large M \) به دو سر پاره خط \( \Large AB \) وصل می‌کنیم و آنگاه دو مثلث قائم الزاویه خواهیم داشت به طوری که:

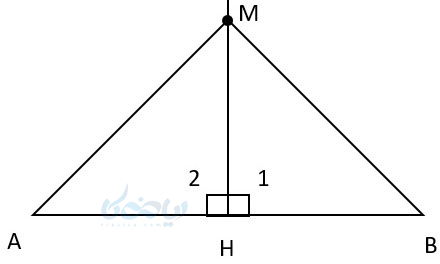
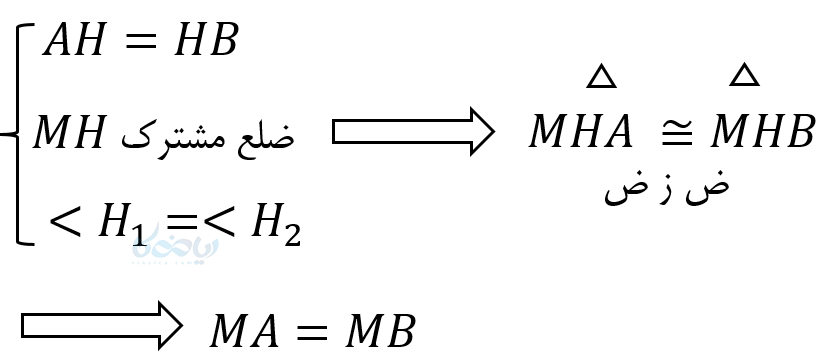
قضیه 2: یک قضیه مهم در ترسیم های هندسی این است که هر نقطه‌ای که فاصله اش از دو سر یک پاره خط به یک اندازه باشد، حتماً روی عمود منصف آن پاره خط قرار دارد.

اثبات: پاره خط \( \Large AB \) را در نظر می‌گیریم و فرض می‌کنیم نقطه \( \Large M \) از دو سر این پاره خط به یک اندازه باشد.
از \( \Large M \) به \( \Large AB \) عمود می‌کنیم. اگر بتوانیم ثابت کنیم \( \Large BH \) \( \Large = \) \( \Large AH \) است، یعنی \( \Large MH \) عمود منصف \( \Large AB \) است و قضیه اثبات می‌شود.

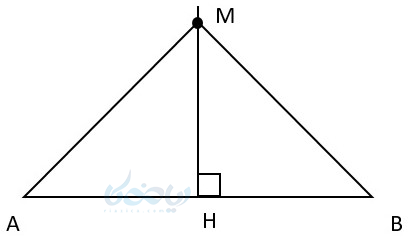
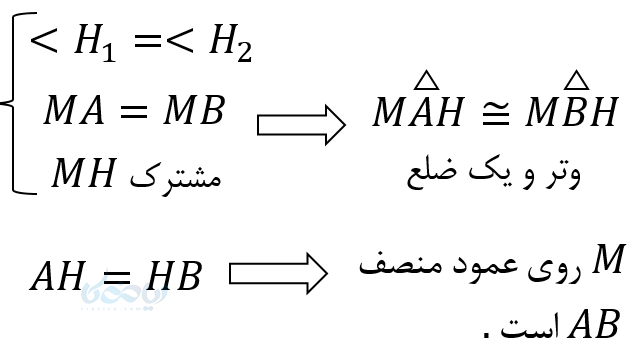
رسم عمود منصف یک پاره خط به کمک آموزش ترسیم های هندسی

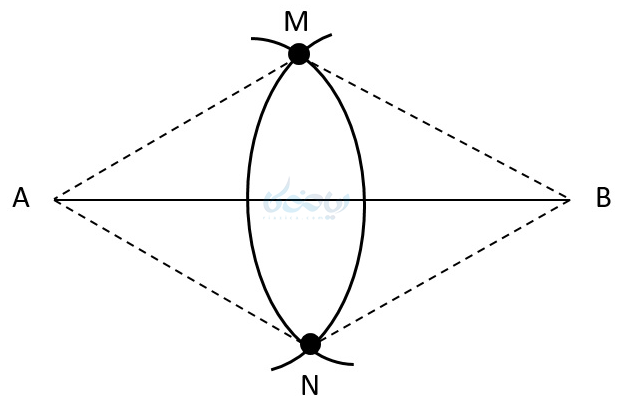
حال با استفاده از قضیه مهم بالا در مورد عمود منصف وبه کمک ترسیم های هندسی  روش‌های رسم عمود منصف را فرا می گیریم. به شکل زیر دقت کنید. برای رسم عمود منصف \( \Large AB \) مراحل زیر را انجام می‌دهیم:

1. ابتدا دهانه پرگار را بیشتر از نصف پاره خط  \( \Large AB \) باز می‌کنیم
2. سپس به مرکز دو سر پاره خط  دو کمان می‌کشیم. همانطور که می‌بینید این دو کمان یکدیگر را در نقاط  \( \Large M \) , \( \Large N \) قطع می‌کنند. چون فاصله , \( \Large M \) ,\( \Large N \)  هر دو تا دو سر پاره خط به یک اندازه است، پس حتماً روی عمود منصف \( \Large AB \) قرار دارند.
3. طبق آنچه در قضیه 2 یاد گرفتیم،  , \( \Large M \) ,\( \Large N \) را به هم وصل می کنیم و این خط عمود منصف پاره خط \( \Large AB \) خواهد بود.

نیمساز و خواص آن با کمک آموزش ترسیم های هندسی

تعریف نیمساز

نیمساز یک زاویه، نیم‌ خطی است که زاویه را به دو قسمت مساوی تقسیم می‌‌کند.

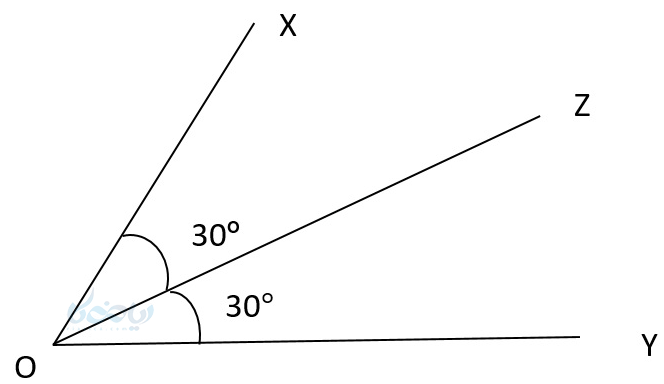
قضیه ۳: اگر خطی روی نیمساز یک زاویه باشد، فاصله اش از دو ضلع زاویه به یک اندازه است.

اثبات: برای اثبات این قضیه زاویه \( \Large XOY \) را در نظر گرفته و نیمساز \( \Large OZ \) را رسم می‌کنیم. نقطهٔ \( \Large M \) روی نیمساز را در نظر می‌گیریم و از آن به دو ضلع زاویه عمود می‌کنیم. ( چون کوتاه‌ترین فاصلهٔ یک نقطه از خط، خط عمود است)

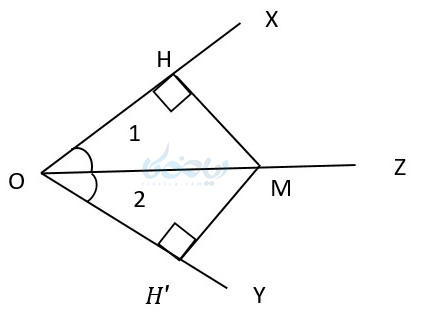
قضیه 4: اگر فاصلهٔ یک نقطه از دو سر پاره خط به یک اندازه باشد، حتماً روی نیمساز آن زاویه قرار دارد.

اثبات: زاویه \( \Large XOY \) را در نظر بگیرید و فرض کنید \( \Large M \) از دو ضلع زاویه به یک اندازه باشد. از \( \Large M \) به راس زاویه وصل می‌کنیم. حال می‌توان اثبات کرد که \( \Large OM \) نیمساز زاویه \( \Large O \) است .

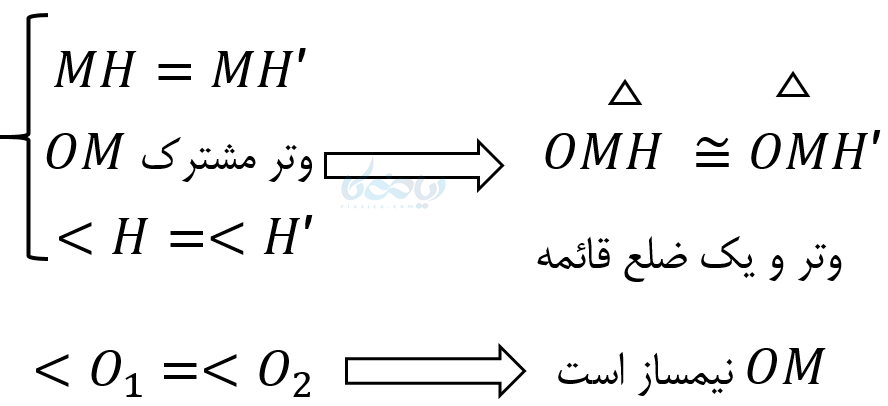
رسم نیمساز یک زاویه

می‌توان به راحتی و با استفاده از آموزش‌های مربوط به ترسیم های هندسی، به راحتی رسم نیمساز را یاد گرفت و روی کاغذ پیاده‌سازی کرد. برای رسم نیمساز مراحل زیر را انجام می‌دهیم:

1. ابتدا دهانه پرگار را به اندازه دلخواه باز می‌کنیم.
2. به مرکز راس زاویه، یک کمان می‌زنیم تا ضلع‌های زاویه را در دو نقطه قطع کند و در نتیجه \( \Large OH` \)\( \Large = \) \( \Large OH \) .
3. حال دهانه پرگار را بیش از نصف پاره خط \( \Large HH` \) باز می‌کنیم.
4. به مرکز \( \Large H \) و ‘\( \Large H \) دو کمان می‌زنیم تا یکدیگر را در نقطه \( \Large M \) قطع کنند. پس \( \Large MH` \)\( \Large = \) \( \Large MH \) خواهد شد.
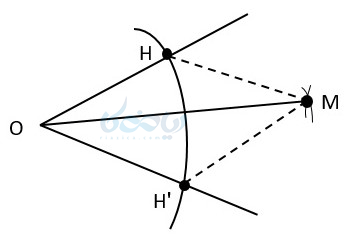
5. حال اگر از \( \Large M \) به \( \Large O \) وصل کنیم، \( \Large OM \) نیمساز زاویه \( \Large O \) است. اما دلیل آن چیست؟

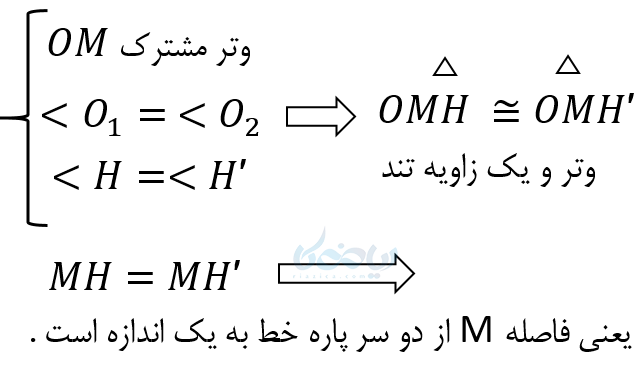
چون دو مثلث \( \Large OMH \) و \( \Large OMH` \) به حالت سه ضلع باهم برابرند و در نتیجه :

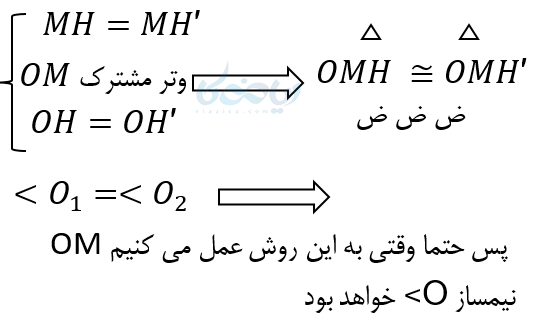
 رسم خطوط عمود و موازی با یک خط

اکنون با استفاده از قضایا و ترسیم های هندسی عمود منصف و نیمساز، می‌خواهیم به روش استدلالی رسم خط عمود و موازی بر یک خط را با هم یاد بگیریم.

1- رسم خط عمود بر یک خط ، از نقطه ای روی آن با استفاده از ترسیم های هندسی

خط \( \Large d \) و نقطهٔ \( \Large M \) که واقع بر آن است را در نظر بگیرید. می‌خواهیم به وسیله پرگار خطی را بر خط \( \Large d \) عمود کنیم که از \( \Large M \) نیز بگذرد . ابتدا به مرکز \( \Large M \) و به شعاع دلخواه یک کمان می‌زنیم تا خط \( \Large d \) را در دو نقطهٔ \( \Large A \) و \( \Large B \)  قطع کند. حال عمود منصف \( \Large AB \) را رسم می‌کنیم. چون \( \Large M \) وسط \( \Large AB \) است پس حتماً از\( \Large M \) گذشته و بر خط \( \Large d \) عمود می‌شود. در نتیجه موفق به رسم خط عمود بر یک خط، از نقطه‌ای روی آن می‌شویم.

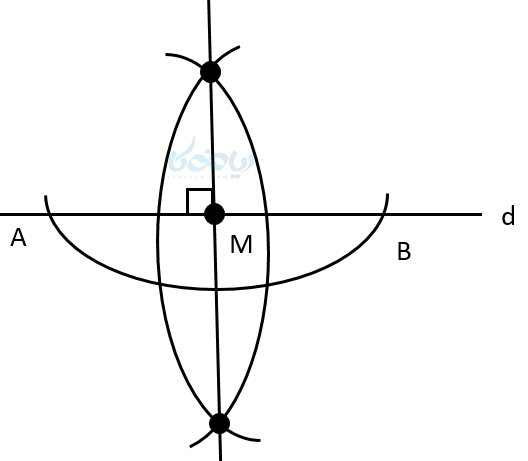
2- رسم خط عمود بر یک خط از نقطه‌ای خارج از آن و به کمک آموزش ترسیم های هندسی

خط \( \Large d \) و نقطه \( \Large M \) که خارج از آن قرار دارد را در نظر می‌گیریم. می‌خواهیم به وسیله پرگار خطی بر \( \Large d \) عمود کنیم که از \( \Large M \) نیز بگذرد. ابتدا دهانهٔ پرگار را از فاصله \( \Large M \) تا \( \Large d \) بیشتر باز می‌کنیم و به مرکز \( \Large M \) یک کمان می‌زنیم تا خط \( \Large d \) را در دو \( \Large A \) و \( \Large B \) قطع کند. پس  \( \Large MA \)\( \Large MB= \) خواهد شد. یعنی فاصله \( \Large M \) از دو سر پاره خط \( \Large AB \)  به یک اندازه است و در نتیجه روی عمود منصف پاره خط AB قرار دارد. حال عمود منصف \( \Large AB \) را رسم می‌کنیم . در نتیجه موفق به رسم خط عمود بر یک خط از نقطه ای خارج آن می‌شویم .

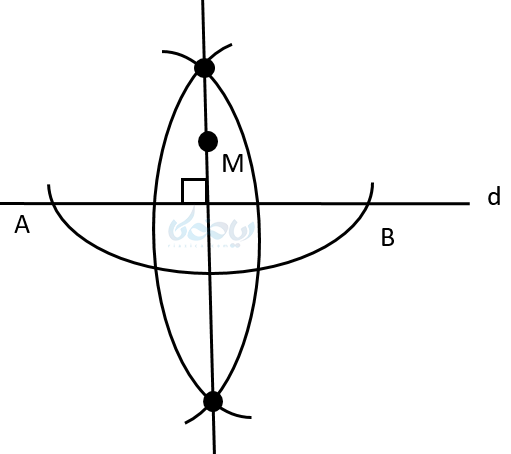
3 – رسم خط عمود موازی با یک خط از نقطه ای خارج از آن

خط \( \Large d \) و نقطه \( \Large M \) که خارج از آن قرار گرفته را در نظر می‌گیریم. حال می‌خواهیم خطی موازی \( \Large d \) رسم کنیم که از \( \Large M \) نیز بگذرد. می‌دانیم دو خط عمود بر یک خط با هم موازی هستند، پس از این خاصیت استفاده می‌کنیم:

1. ابتدا با استفاده از پرگار مانند قسمت 2 خطی عمود بر \( \Large d \) رسم می کنیم که از \( \Large M \) بگذرد تا خط \( \Large d’ \) بدست آید.
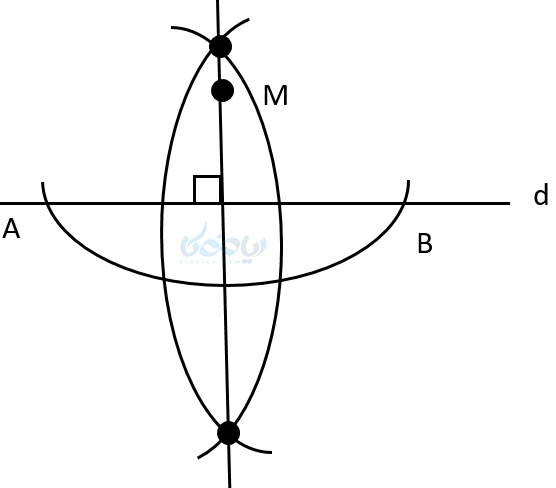
2. حال مانند قسمت اول به خط \( \Large d’ \) و به نقطه \( \Large M \) یک خط عمود می‌کنیم تا خط \( \Large d” \) به وجود آید.(مادراینجاکمانهای اضافی بالا را پاک کردیم وقسمت دوم را اجرا کردیم.)
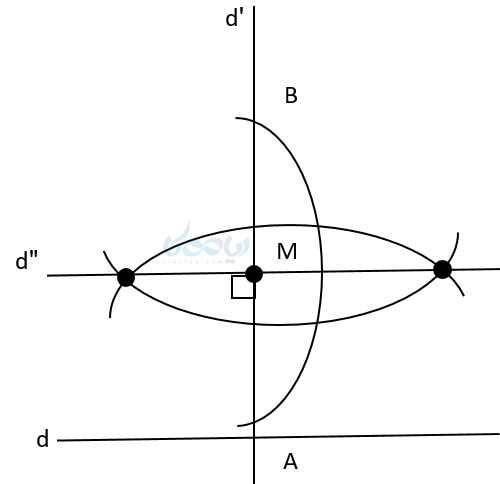
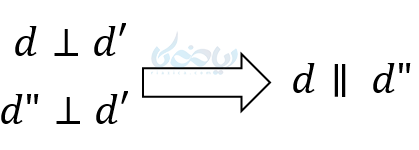
3. \( \Large d” \) و \( \Large d \) هر دو به \( \Large d’ \) عمود هستند، پس حتما با هم موازی خواهند بود. در نتیجه موفق به رسم خط عمود موازی با یک خط از نقطه ای خارج از آن می‌شویم.

آخر درس آموزش ترسیم های هندسی

ترسیم های هندسی از جذاب‌ترین بخش‌های آموزش ریاضیات پایه دهم است. تا جایی که حتی تدریس این مبحث مهم بعلت وجود نکات زیبای هندسی، برای معلمین نیز شیرین است.

درصورتی که هر سوالی از این بخش دارید، می‌توانید آن را در بخش دیدگاه‌ها در پایین همین صفحه بنویسید. کارشناسان ما در ریاضیکا پاسخ سوال شما را خواهند داد.