آموزش ریاضی پایه نهم
تجزیه ریاضی نهم 🔑4️⃣ – ۴ روش کلیدی یادبگیر!
در درسنامۀ تجزیه ریاضی نهم ابتدا منظور از تجزیهٔ یک عبارت جبری را بیان میکنیم. در ادامه، با استفاده از فاکتورگیری و اتحادهای مربع دو جملهای، مزدوج و جمله مشترک، نحوهٔ تجزیهٔ عبارات جبری مختلف را میبینیم. در انتها نیز، تجزیۀ عبارات جبری را با استفاده از ترکیب روشهایی که آموختیم، بررسی میکنیم. سعی میکنیم با حل مثالهای مختلف از مبحث تجزیه ریاضی نهم در درک بهتر آن به شما کمک کنیم. با ما تا انتهای درسنامه همراه باشید.
تجزیه عبارت جبری
در صورتی که یک چند جملهای را به صورت حاصل ضرب دو یا چند عبارت بنویسیم، آن چند جملهای را تجزیه کردهایم. روشهای مختلفی برای تجزیۀ یک چند جملهای وجود دارد که در این درس چهار مورد از آن ها را خواهیم آموخت:
- تجزیه با استفاده از فاکتورگیری
- تجزیه با استفاده از مربع دو جملهای
- تجزیه با استفاده از اتحاد مزدوج
- تجزیه با استفاده از اتحاد جمله مشترک
در ادامه، هر یک از این دو روش را بررسی خواهیم کرد.
تجزیه با فاکتورگیری
خاصیت پخشی میگوید حاصل عبارت \(\Large x(y+z)\) برابر است با \(\Large xy+xz\). بنابراین اگر یک چندجملهای داشته باشیم که به صورت \(\Large xy+xz\) باشد، میتوانیم آن را به صورت حاصل ضرب \(\Large x(y+z)\) تجزیه کنیم. \(\Large x\) در این عبارت، بزرگترین عامل مشترک دو جمله است. اصطلاحاً میگوییم \(\Large x\) را فاکتور گرفتهایم. در واقع در فاکتورگیری، تک تک جملات را بر عامل مشترکشان تقسیم میکنیم. برای پیدا کردن بزرگترین عامل مشترک دو جمله کافی است تا ب.م.م ضرایب را در کوچکترین توان متغیرهای مشترک بین جملات ضرب کنیم. مثلاً عبارت زیر را در نظر بگیرید:
\(\LARGE 9x+6x^2\)
ب.م.م دو عدد \(\Large 9\) و \(\Large 6\) برابر است با \(\Large 3\). متغیر \(\Large x\) نیز در هر دو عبارت مشترک بوده و کوچکترین توان آن برابر است با \(\Large 1\). بنابراین بزرگترین عامل مشترک دو جملۀ \(\Large 9x\) و \(\Large 6x^2\) برابر است با \(\Large 3x\). در نتیجه میتوانیم عبارت \(\Large 9x+6x^2\) را به صورت زیر تجزیه کنیم:
\(\LARGE 3x(3+2x)\)
به مثال بعدی از درسنامۀ تجزیه ریاضی نهم توجه کنید.
مثال از تجزیه با فاکتور گیری
مثال 1: عبارت \(\Large 8yz^2+20y^2z^3-12yz^4\) را با استفاده از فاکتورگیری تجزیه کنید.
حل: تفاوتی نمیکند که با دو جمله سر و کار داشته باشیم یا چند جمله. کافی است بزرگترین عامل مشترک جملات را پیدا کنیم. ب.م.م سه عدد \(\Large 8\) و \(\Large 20\) و \(\Large 12\) برابر است با \(\Large 4\). از طرفی کوچکترین توان \(\Large y\) در هر عبارت برابر است با \(\Large 1\) و کوچکترین توان \(\Large z\) در هر عبارت برابر است با \(\Large 2\). بنابراین بزرگترین عامل مشترک این سه جمله برابر است با \(\Large 4yz^2\). در نتیجه میتوانیم \(\Large 4yz^2\) را فاکتور بگیریم. یعنی باید تمام جملات را بر \(\Large 4yz^2\) تقسیم کرده و عبارت داده شده در مسئله را به صورت زیر بازنویسی کنیم:
\(\LARGE 4yz^2(2+5yz-3z^2)\)
به مثال بعدی از درسنامۀ تجزیه ریاضی نهم توجه کنید.
مثال 2 عبارت \(\Large 6xyz+3y+9yz^2\) را با استفاده از فاکتورگیری تجزیه کنید.
حل: ب.م.م سه عدد \(\Large 6\) و \(\Large 3\) و \(\Large 9\) برابر است با \(\Large 3\). از طرفی کوچکترین توان \(\Large x\) بین سه عبارت برابر است با \(\Large 0\) و کوچکترین توان \(\Large y\) بین سه عبارت برابر است با \(\Large 1\) و کوچکترین توان \(\Large z\) بین سه عبارت برابر است با \(\Large 0\). بنابراین بزرگترین عامل مشترک این سه جمله برابر است با \(\Large 3y\). در نتیجه میتوانیم \(\Large 3y\) را فاکتور بگیریم. یعنی باید تمام جملات را بر \(\Large 3y\) تقسیم کرده و عبارت داده شده در مسئله را به صورت زیر بازنویسی کنیم:
\(\LARGE 3y(2xz+1+3z^2)\)
حواستان به یک نکتۀ خیلی مهم باشد! وقتی از عبارت \(\Large 3y\)، عبارت \(\Large 3y\) را فاکتور میگیریم، حاصل برابر با \(\Large 1\) میشود، نه \(\Large 0\). زیرا همان طور که گفتیم، در فاکتورگیری، دو عبارت را بر هم تقسیم میکنیم، کم نمیکنیم. زمانی که \(\Large 3y\) را بر \(\Large 3y\) تقسیم میکنیم، حاصل برابر با \(\Large 1\) میشود. در نتیجه وقتی از \(\Large 3y\)، عبارت \(\Large 3y\) را فاکتور گرفتیم، عدد \(\Large 1\) باقی ماند.
تجزیه با استفاده از اتحاد مربع دو جمله ای
میتوانیم برخی از چندجملهایها را با استفاده از اتحاد مربع دو جمله ای تجزیه کنیم. یعنی داریم:
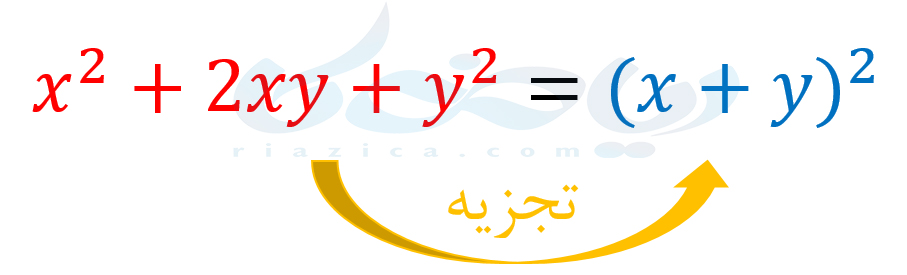
از آنجاییکه \(\Large (x+y)^2\) همان \(\Large (x+y)(x+y)\) است، در واقع چند جمله ای \(\Large x^2+2xy+y^2\) را به حاصل ضرب دو عبارت تجزیه کردهایم. برای تفاضل هم می توانیم مشابه همین کار را انجام دهیم. یعنی داریم:
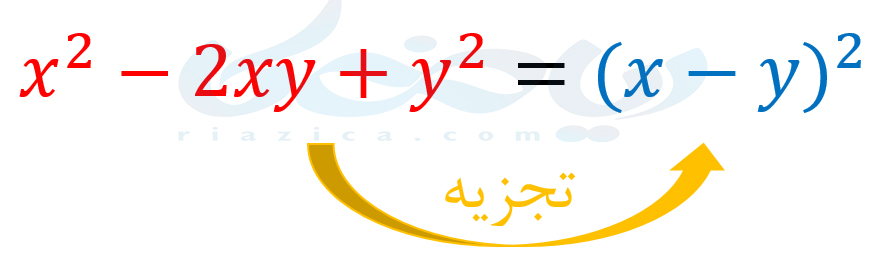
بنابراین اگر سه جمله داشتیم که دوتای آنها مربع کامل بودند، احتمال میدهیم که بتوان از اتحاد مربع دو جمله ای استفاده کرد. برای اینکه کمی بیشتر با این نوع تجزیه آشنا شوید، به مثالهای بعدی از درسنامۀ تجزیه ریاضی نهم توجه کنید.
مثال از تجزیه با استفاده از اتحاد مربع دو جمله ای
مثال 3: عبارت \(\Large x^2+10x+25\) را تجزیه کنید.
حل: یک جمله ای \(\Large x^2\) مربع کامل بوده و برابر است با توان دوم \(\Large x\). یک جمله ای \(\Large 25\) نیز مربع کامل بوده و برابر است با توان دوم \(\Large 5\). از طرفی \(\Large 10x\) برابر است با دو برابر حاصل ضرب \(\Large x\) در \(\Large 5\). یعنی عبارت \(\Large x^2+10x+25\) را میتوانیم به صورت زیر بازنویسی کنیم:
\(\LARGE x^2+2 \times x \times 5 +5^2\)
عبارت بالا برابر است با مربع \(\Large (x+5)\). یعنی جواب مسئله برابر است با \(\Large (x+5)^2\).
تجزیه با استفاده از اتحاد مزدوج
از اتحاد مزدوج نیز میتوان برای تجزیۀ اتحادهای جبری استفاده کرد. یعنی داریم:
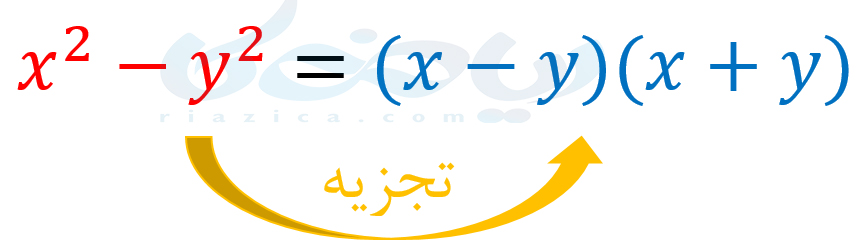
بنابراین اگر در یک عبارت جبری، دو مربع کامل داشتیم که از هم کم شده بودند (مانند طرف چپ عبارت بالا) میتوانیم آن را به صورت حاصل ضرب مجموع در تفاضل ریشۀ دومشان (مانند طرف راست عبارت بالا) بنویسیم. به بیان سادهتر، زمانی که دو مربع کامل از هم کم شده بودند، عبارت داده شده را به صورت حاصل ضرب دو دوجملهای که یکی از آنها حاصل جمع است و دیگری حاصل تفریق، مینویسیم. به مثالهای بعدی از درسنامۀ تجزیه ریاضی نهم توجه کنید.
مثال از تجزیه ریاضی نهم
مثال 4: عبارت \(\Large 4x^2-25\) را با استفاده از اتحاد مزدوج تجزیه کنید.
حل: عدد \(\Large 25\)، توان دوم عدد \(\Large 5\) است و عبارت \(\Large 4x^2\)، توان دوم عبارت \(\Large 2x\) است. بنابراین طبق اتحاد مزدوج داریم:
\(\Large 4x^2-25=(2x-5)(2x+5) \)
به مثال بعدی از درسنامۀ تجزیه ریاضی نهم توجه کنید.
مثال 5: عبارت \(\Large (3x-2)^2-(2x+1)^2\) را با استفاده از اتحاد مزدوج تجزیه کنید.
حل: عبارت \(\Large (3x-2)^2\)، توان دوم عدد \(\Large (3x-2)\) است و عبارت \(\Large (2x+1)^2\)، توان دوم عبارت \(\Large (2x+1)\) است. بنابراین طبق اتحاد مزدوج داریم:
\(\LARGE (3x-2)^2-(2x+1)^2 \)
\( =((3x-2)-(2x+1))((3x-2)+(2x+1)) \)
\(\LARGE =(x-3)(5x-1) \)
به قسمت بعدی از درسنامۀ تجزیه ریاضی نهم توجه کنید.
تجزیه با استفاده از اتحاد جمله مشترک
همان طور که از اتحاد مربع دو جمله ای و اتحاد مزدوج برای تجزیۀ عبارات جبری استفاده کردیم، از اتحاد جمله مشترک نیز میتوانیم استفاده کنیم. یعنی داریم:
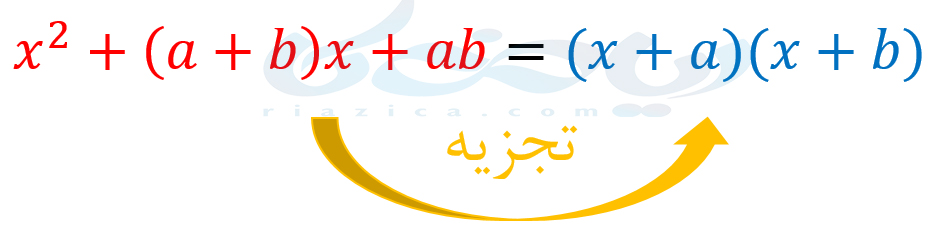
به عبارت دیگر اگر اگر یک چند جملهای درجۀ دو با متغیر \(\Large x\) و ضرایب حقیقی داشتیم و میخواستیم آن را با استفاده از اتحاد جمله مشترک تجزیه کنیم، باید به دنبال دو عدد حقیقی باشیم که مجموع آن دو عدد برابر با ضریب \(\Large x\) و حاصل ضرب آن دو عدد برابر با مقدار ثابت آن چند جملهای باشد. به بیان ساده تر،اگر سه جمله داشته باشیم که یکی از آنها مربع کامل باشد، حدس میزنیم که بتوان از اتحاد جمله مشترک استفاده کرد. برای اینکه بهتر متوجه شوید، به مثالهای بعدی از درسنامۀ تجزیه ریاضی نهم توجه کنید.
مثال از تجزیه ریاضی نهم
مثال 6: عبارت \(\Large x^2+x-6\) را با استفاده از اتحاد جمله مشترک تجزیه کنید.
حل: چند جملهای درجۀ دو با متغیر \(\Large x\) داریم. باید دو عدد پیدا کنیم که مجموعشان برابر با \(\Large 1\) و حاصل ضربشان برابر با \(\Large -6\) شود. دو عدد \(\Large 3\) و \(\Large -2\) شرایطی که میخواستیم را دارند. بنابراین داریم:
\(\LARGE x^2+x-6\)
\(\LARGE =(x+3)(x-2)\)
به مثال بعدی از درسنامۀ تجزیه ریاضی نهم توجه کنید.
مثال 7: عبارت \(\Large y^2+3y+2\) را با استفاده از اتحاد جمله مشترک تجزیه کنید.
حل: چند جملهای درجۀ دو با متغیر \(\Large y\) داریم. باید دو عدد پیدا کنیم که مجموعشان برابر با \(\Large 3\) و حاصل ضربشان برابر با \(\Large 2\) شود. دو عدد \(\Large 1\) و \(\Large 2\) شرایطی که میخواستیم را دارند. بنابراین داریم:
\(\LARGE y^2+3y+2\)
\(\LARGE =(y+1)(y+2)\)
تجزیه با ترکیب روشها
گاهی برای تجزیۀ یک چند جمله ای لازم است که از ترکیب چند روش و یا چند اتحاد استفاده کنیم. مثلاً گاهی لازم است که ابتدا چند جملهای داده شده را فاکتورگیری کرده و سپس آن را به صورت مربع کامل در آوریم. برای اینکه بهتر متوجه شوید، به مثال بعدی از درسنامه تجزیه ریاضی نهم توجه کنید.
مثال از تجزیه ریاضی نهم
مثال 8: عبارت \(\Large 3x^2y-6xy+3y\) را تجزیه کنید.
حل: ابتدا \(\Large 3y\) را فاکتور میگیریم:
\(\LARGE 3y(x^2-2x+1)\)
حال میتوانیم عبارت درون پرانتز را به صورت مربع کامل بنویسیم؛ زیرا \(\Large x^2\) همان توان دوم \(\Large x\) است، \(\Large 1\) همان توان دوم عدد \(\Large 1\) است و \(\Large 2x\) همان دو برابر حاصل ضرب \(\Large x\) در \(\Large 1\) است. بنابراین عبارت بالا به صورت زیر در میآید:
\(\LARGE 3y(x-1)^2\)
در مثال بعدی از درسنامۀ تجزیه ریاضی نهم با استفاده از فاکتورگیری و اتحاد جمله مشترک، یک عبارت جبری را تجزیه میکنیم.
مثال 9: عبارت \(\Large ax^2+11ax+28a\) را تجزیه کنید.
حل: بزرگترین عامل مشترک بین سه جمله، متغیر \(\Large a\) است. بنابراین میتوانیم آن را فاکتور بگیریم تا عبارت داده شده به صورت زیر درآید:
\(\LARGE a(x^2+11x+28)\)
حال میتوانیم عبارت درون پرانتز را با استفاده از اتحاد جمله مشترک تجزیه کنیم. برای این کار کافی است به دنبال دو عدد باشیم که مجموعشان برابر با \(\Large 11\) و حاصل ضربشان برابر با \(\Large 28\) باشد. دو عدد \(\Large 4\) و \(\Large 7\) این شرایط را دارند. بنابراین داریم:
\(\LARGE ax^2+11ax+28a\)
\(\LARGE =a(x^2+11x+28)\)
\(\LARGE =a(x+4)(x+7)\)
برای یادگیری بیشتر این مطلب حتما درسنامه تجزیه عبارت های جبری به ۴ روش را مطالعه کنید.
ویدیو آموزش تجزیه ریاضی نهم
در این ویدیو یاد خواهید گرفت چگونه عبارت های جبری خاص را به کمک اتحاد جمله مشترک را تجزیه کنید.
زنگ آخر کلاس تجزیه ریاضی نهم
در درسنامهای که از ریاضی نهم خواندیم، ابتدا منظور از تجزیۀ یک عبارت جبری را بیان کردیم. سپس، تجزیۀ عبارات جبری را با استفاده از فاکتورگیری، اتحاد مربع دو جمله ای، اتحاد مزدوج و اتحاد جمله مشترک بررسی کردیم. در انتهای درسنامه نیز دیدیم که گاهی برای تجزیۀ یک عبارت جبری لازم است که از ترکیب چند روشی که خواندیم استفاده کنیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با این مبحث دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





توضیحات رو نتونستن خوب استفاده کنم
ولی از نمونه سوالات که سبز رنگ بود استفاده کردم ممنون
با سلام وعرض ادب
ممنون از نظر شما
واقعا ممنونم بسیار عالی بود و خیلی بدردم خورد
با سلام وعرض ادب
ممنون از شما وتوجه شما خوشحالیم مفید واقع شده
خوب بود
با سلام وعرض ادب
ممنون از نظر شما
با سلام ..بسیار مفید و کاربردی بود ممنون
با سلام واحترام
خوشحالیم که مفید واقع شده
عالییییی
با سلام و عرض ادب
ممنون از شما دوست عزیز
خیلی خوب توضیح داده بودین کامل یاد گرفتم?
خیلی خیلی ممنون
با سلام واحترام
خدا روشکر
عالی بود خیلی ممنون هم توضیحات و همنمونه سوالات ♡
سلام وقت بخیر خیلی ممنون بسیار کامل بود خسته نباشید
با سلام
خرسندیم مفید بوده برای شما
ایکس به توان۲زِدمنهای ایگرگ به توان۲ زِد چی میشه نهمم
با سلام دوست عزیز
کافیه از z فاکتور بگیرید وبعد داخل پرانتز ازاتحاد مزدوج تجزیه کنید
X²+3x_10
جواب چی میشه
عالی
سپاس از شما??
این یک اتحاد مشترک هست
چه اعدادی جمعشون میشه 3 و ضربشون میشه 10- ؟
اعداد 5+ و 2- هستند
حالا جواب = (x+5)(x-2) وتمام
با سلام ممنون از پاسخگویی شما
aب توان۴ منهای ۵aب توان ۲بعلاوه ۴؟
«نهم»
خیلی عالی بود ممنون از توضیحات شما
با سلام دوست عزیز
ممنون از نظر لطف شما
بسیار عالی ممنون از راهنمایی شما
باسلام وادب
ممنون از نظر شما
خوب بود
خوب بود
عالی بود
سلام دوست عزیز
ممنون از نظر شما
عالی بود من تجزیه ها را یاد گرفتم ممنون
با رادیکال چطور حل کنیم ؟
با سلام
اگه منظورتون تجزیه هست ما با ضرایب صحیح تجزیه رو انجام میپیم
سلام بسیار عالی بود من خیلی خوب یاد گرفتم سپاسگزارم از مطلب مفیدتون
با سلام وادب
خدا رو شاکریم که مفید بوده
سلام
واقعا خیلی عالی بود ممنونم بابت زحماتتون
با سلام
خدا رو شکر که برای شما مفید بوده
خیلی خوب بود
خیلی عالی بود به راحتی متوجه مطلب شدم
با سلام وادب
ممنون از لطف شما
خیلی عالی بود به راحتی متوجه مطلب شدم فقط اگه بتونید مطالب رو با مثال های بیشتر و گسترده تر توضیح بدید عالی میشه
با سلام
ممنون از پیشنهاد شما
سلام عالی
عالی بود
سلام دوست عزیز
ممنون از لطف شما
توضیحات عالی و کامل
متشکر
اصلا عالی