آموزش ریاضی پایه هفتم
بردار های مساوی و قرینه ریاضی هفتم ➡️⬅️ + تصاویر مفهومی!
در درسنامهٔ بردار های مساوی و قرینه ریاضی هفتم بررسی میکنیم که در چه شرایطی دو بردار با یکدیگر مساوی هستند و یا قرینهٔ یکدیگرند. سعی میکنیم با حل مثال، به درک بهتر شما از این مبحث کمک کنیم. بهتر است پیش از مطالعهٔ این درسنامه، درسنامهٔ پاره خط جهت دار ریاضی هفتم را مطالعه کنید.
بردارهای مساوی
دو برداری که همراستا، هماندازه و همجهت هستند، با یکدیگر برابرند. باید دقت کرد که به دو برداری که با یکدیگر موازی باشند یا روی یک خط قرار داشته باشند، همراستا میگوییم (دلیل این امر به تعریف بردار اقلیدسی و زاویهای که بردار با محورها میسازد بر میگردد که در این مقطع به آن نمی پردازیم). بنابراین، دو بردار \(\Large \overrightarrow{AB}\) و \(\Large \overrightarrow{CD}\) که در شکل زیر رسم شدهاند، با یکدیگربرابرند؛ زیرا هم اندازهاند، با یکدیگر موازیاند و همجهت هستند:
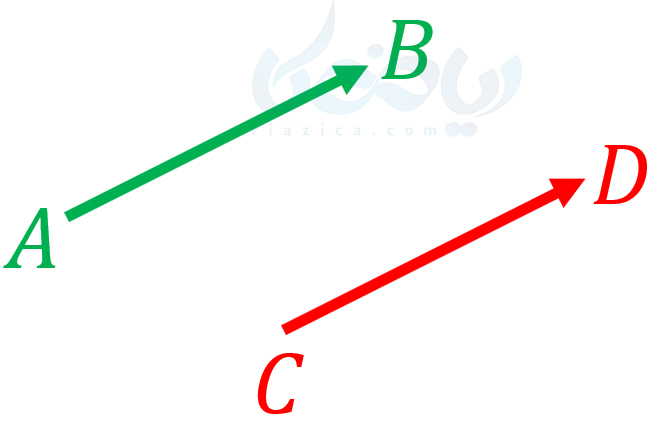
در ادامهٔ درسنامهٔ بردار های مساوی و قرینه ریاضی هفتم مثالهایی از بردارهای برابر خواهیم دید.
مثال از بردار های برابر
مثال 1 بردار های مساوی و قرینه ریاضی هفتم: در شکل زیر، روی محور، برداری برابر با بردار \(\Large \overrightarrow{OA}\) رسم کنید.
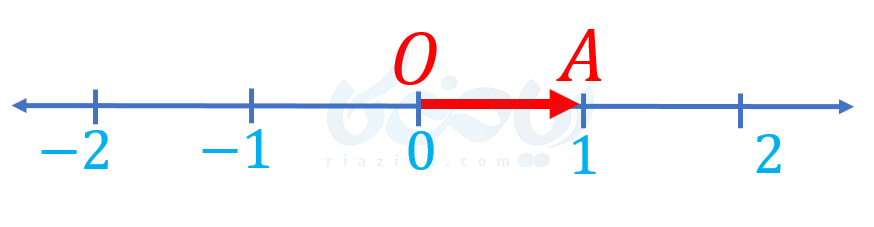
حل: از آنجاییکه تمام بردارهای روی محور، روی یک خط قرار دارند، هر برداری که روی محور رسم کنیم، با بردار \(\Large \overrightarrow{OA}\) همراستاست. بنابراین، اگر برداری همجهت و هماندازه با بردار \(\Large \overrightarrow{OA}\) رسم کنیم، با آن برابر خواهد بود. برای حفظ جهت، کافی است، برداری رسم کنیم که در جهت مثبت محور باشد. برای یکسان بودن اندازه نیز کافی است برداری به طول واحد رسم کنیم. بنابراین، به صورتهای مختلفی میتوان برداری برابر با بردار \(\Large \overrightarrow{OA}\) رسم کرد. در شکل زیر، یکی از این بردارها را که بردار \(\Large \overrightarrow{CD}\) است، رسم کردهایم:
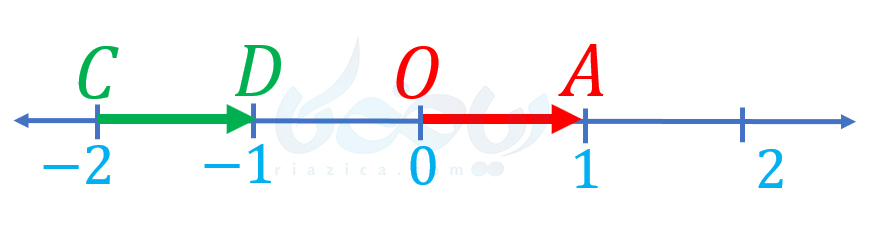
اگر برداری رسم میکردیم که ابتدای آن روی نقطهٔ \(\Large -1\) و انتهای آن روی نقطهٔ \(\Large 0\) قرار داست، بازهم با بردار \(\Large \overrightarrow{OA}\) برابر بود. البته بردارهای برابر با \(\Large \overrightarrow{OA}\) تنها به این دو برداری که اشاره کردیم محدود نمیشوند. کافی است از هر نقطه روی محور شروع کرده و یک واحد در جهت مثبت محور حرکت کنیم؛ بردار متناظر با حرکت ما، با بردار \(\Large \overrightarrow{OA}\) برابر خواهد بود. بنابراین میتوان بیشمار بردار برابر با بردار \(\Large \overrightarrow{OA}\) روی محور رسم کرد.
مثال از درسنامهٔ بردارهای مساوی و قرینه ریاضی هفتم
مثال 2 بردار های مساوی و قرینه ریاضی هفتم: در شکل زیر، چهار بردار طوری کنار هم قرار گرفتهاند که تشکیل یک متوازیالاضلاع میدهند. آیا دو بردار \(\Large \overrightarrow{AB}\) و \(\Large \overrightarrow{CD}\) با یکدیگر برابرند؟ دو بردار \(\Large \overrightarrow{BC}\) و \(\Large \overrightarrow{AD}\) چه طور؟
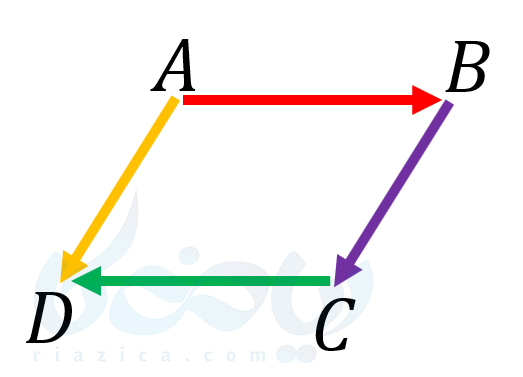
حل: پارهخط های \(\Large AB\) و \(\Large CD\) با یکدیگر موازیاند. بنابراین، بردارهای \(\Large \overrightarrow{AB}\) و \(\Large \overrightarrow{CD}\) همراستا هستند. اما جهت دو بردار \(\Large \overrightarrow{AB}\) و \(\Large \overrightarrow{CD}\) با یکدیگر متفاوت است. بنابراین، دو بردار \(\Large \overrightarrow{AB}\) و \(\Large \overrightarrow{CD}\) با یکدیگر برابر نیستند. اما بردارهای \(\Large \overrightarrow{BC}\) و \(\Large \overrightarrow{AD}\) هم در یک راستا و هم در یک جهت قرار دارند. بنابراین، دو بردار \(\Large \overrightarrow{BC}\) و \(\Large \overrightarrow{AD}\) با یکدیگر برابرند.
بردارهای قرینه
با بردارهای قرینه در درسنامهٔ پاره خط جهت دار ریاضی هفتم آشنا شدیم. همان طور که گفتیم، بردارهایی که هماندازهاند و در یک راستا قرار دارند اما در جهت عکس یکدیگر هستند، قرینهٔ یکدیگرند. در این درسنامه سعی داریم به بررسی مثالهای بیشتری از بردارهای قرینه بپردازیم.
مثال از درسنامهٔ بردارهای مساوی و قرینه ریاضی هفتم
مثال 3 بردار های مساوی و قرینه ریاضی هفتم: در شکل زیر، روی محور، برداری قرینهٔ بردار \(\Large \overrightarrow{AO}\) رسم کنید.

حل: هر برداری که روی محور قرار داشته باشد، با بردار \(\Large \overrightarrow{AO}\) همراستاست. بنابراین، اگر برداری هماندازه و در خلاف جهت با بردار \(\Large \overrightarrow{AO}\) رسم کنیم، قرینهٔ آن خواهد بود. برای اینکه برداری در عکس جهت بردار \(\Large \overrightarrow{AO}\) رسم کنیم، کافی است برداری در نظر بگیریم که در جهت مثبت محور باشد. برای یکسان بودن اندازه نیز کافی است برداری به طول واحد رسم کنیم. بنابراین، به صورتهای مختلفی میتوان برداری قرینهٔ بردار \(\Large \overrightarrow{AO}\) رسم کرد. در شکل زیر، یکی از این بردارها را که بردار \(\Large \overrightarrow{CD}\) است، رسم کردهایم:
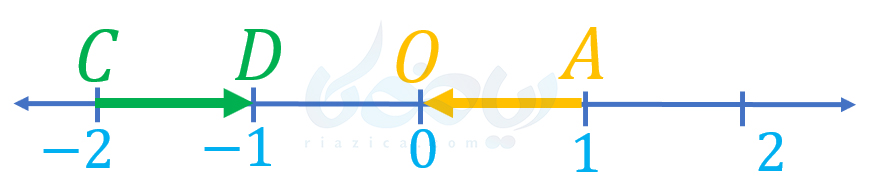
مثال از درسنامهٔ بردار های مساوی و قرینه ریاضی هفتم
مثال 4 از بردار های مساوی و قرینه ریاضی هفتم: در شکل زیر شش بردار طوری کنار هم قرار گرفتهاند که یک ششضلعی منتظم تشکیل شده است. بردارهای مساوی و قرینه را بیابید.
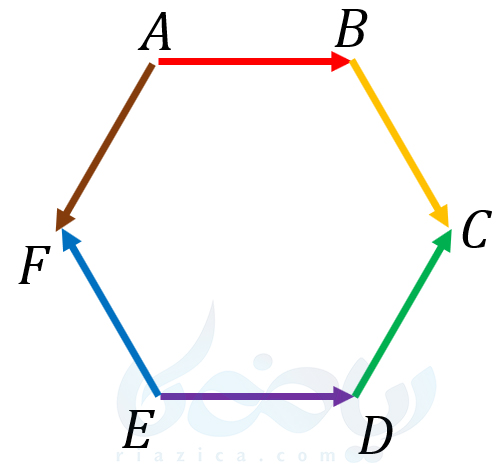
حل: هم بردارهای برابر و هم بردارهای قرینه باید هماندازه و در یک راستا باشند. چون بردارها تشکیل یک ششضلعی منتظم دادهاند، اندازهٔ همهٔ آنها با هم برابر است. بنابراین نیازی به چک کردن برابری اندازهها نیست. اما تنها بردارهایی میتوانند با یکدیگر همراستا باشند که با یکدیگر موازی هستند. بنابراین، کافی است تنها جهت بردارهای موازی را با یکدیگر مقایسه کنیم. اگر در یک جهت بودند، دو بردار برابر هستند، اگر در خلاف جهت هم بودند، قرینهٔ یکدیگرند.
- دو بردار \(\Large \overrightarrow{AB}\) و \(\Large \overrightarrow{ED}\) با یکدیگر برابرند؛ زیرا در یک جهت هستند.
- دو بردار \(\Large \overrightarrow{BC}\) و \(\Large \overrightarrow{EF}\) قرینهٔ یکدیگرند؛ زیرا در خلاف جهت هم هستند.
- دو بردار \(\Large \overrightarrow{DC}\) و \(\Large \overrightarrow{AF}\) قرینهٔ یکدیگرند؛ زیرا در خلاف جهت هم هستند.
زنگ آخر کلاس بردارهای مساوی و قرینه ریاضی هفتم
در درسنامهای که از ریاضی هفتم خواندیم، بردارهای برابر و قرینه را بررسی کردیم. همان طور که دیدید، دو برداری که هماندازه، همجهت و همراستا هستند، با یکدیگر برابرند. دو برداری هم که با یکدیگر هماندازه و همراستا هستند اما در خلاف جهت یکدیگرند، قرینهٔ هم هستند. سعی کردیم با حل مثالهای مختلف به درک بهتر شما از مبحث کمک کنیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با بردار های مساوی و قرینه ریاضی هفتم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.