آموزش ریاضی پایه دوازدهم تجربی
تابع مشتق 👩🎓💢 ریاضی دوازدهم تجربی – کاملترین آموزش ممکن!
در درسنامهٔ مشتق دوازدهم تجربی، با مفهوم مشتق آشنا شدیم. در این درسنامه قصد داریم مفهوم جدیدی به نام تابع مشتق را معرفی کنیم. علاوه بر معرفی، مشتق برخی از توابع خاص را نیز محاسبه میکنیم. از مشتق این توابع خاص برای محاسبهٔ تابع مشتق بسیاری از توابع دیگر استفاده خواهیم کرد.
تابع مشتق
در صورتی که \(\Large x \) جزء دامنهٔ تابع \(\Large f(x) \) باشد و \(\Large f \) در \(\Large x \) مشتق پذیر باشد، تابع مشتق \(\Large f \) در \(\Large x \) را به صورت زیر تعریف میکنیم:
\(\LARGE f'(x)=\lim\limits_{h\to 0} \frac{f(x+h)-f(x)}{h} \)
مثال 1: اگر \(\Large f(x)=\frac{1}{\sqrt{x}} \) باشد، \(\Large f’ \) و دامنۀ \(\Large f’ \) را به دست آورید.
حل: طبق تعریف، \(\Large f'(x) \) برابر است با:
\(\LARGE f'(x)=\lim\limits_{h\to 0} \frac{f(x+h)-f(x)}{h} \)
\(\LARGE =\lim\limits_{h\to 0} \frac{\frac{1}{\sqrt{x+h}}-\frac{1}{\sqrt{x}}}{h} \)
\(\LARGE =\lim\limits_{h\to 0} \frac{\sqrt{x}-\sqrt{x+h}}{h \sqrt{x(x+h)}} \)
\(\LARGE =\lim\limits_{h\to 0} \frac{(\sqrt{x}-\sqrt{x+h})(\sqrt{x}+\sqrt{x+h})}{h \sqrt{x(x+h)}(\sqrt{x}+\sqrt{x+h})} \)
\(\LARGE =\lim\limits_{h\to 0} \frac{x-(x+h)}{h \sqrt{x(x+h)}(\sqrt{x}+\sqrt{x+h})} \)
\(\LARGE =\lim\limits_{h\to 0} \frac{-h}{h \sqrt{x(x+h)}(\sqrt{x}+\sqrt{x+h})} \)
\(\LARGE =\lim\limits_{h\to 0} \frac{-1}{ \sqrt{x(x+h)}(\sqrt{x}+\sqrt{x+h})} \)
\(\LARGE =\lim\limits_{h\to 0} \frac{-1}{ \sqrt{x^2}(\sqrt{x}+\sqrt{x})} \)
\(\LARGE =\lim\limits_{h\to 0} \frac{-1}{ \sqrt{x^2}(2\sqrt{x})} \)
\(\LARGE =\lim\limits_{h\to 0} \frac{-1}{ 2\sqrt{x^3}} \)
محاسبه تابع مشتق برخی از توابع
بسیاری از عباراتی که با آنها سر و کار داریم تشکیل شدهاند از ضرایب ثابت، عبارات با توانهای گویا، جمع و تفریق و ضرب و تقسیم توابع و همچنین ترکیب آنها. اگر از پیش، رابطهای برای محاسبه مشتق هر یک از آنها داشته باشیم، میتوانیم مشتق اکثر عبارات جبری را بدون محاسبهٔ حد که در تعریف مشتق معرفی کردیم به دست آوریم. در ادامه تابع مشتق عبارات جبری پر کاربرد را به دست میآوریم.
مشتق تابع ثابت
مشتق تابع ثابت در هر نقطه برابر با صفر است. در واقع اگر \(\Large f(x)=c \) باشد که \(\Large c \) یک ضریب ثابت است، خواهیم داشت:
\(\LARGE f'(x)=\lim\limits_{h\to 0} \frac{f(x+h)-f(x)}{h} \)
\(\LARGE =\lim\limits_{h\to 0} \frac{c-c}{h}=0 \)
مثال 2: مشتق توابعی مانند \(\Large f(x)=4 \) یا \(\Large g(x)=-\frac{\sqrt{2}}{3} \) برابر با صفر است.
مشتق تابع با ضریب ثابت
اگر \(\Large y=af(x) \) باشد که \(\Large a \) یک ضریب ثابت است، مشتق \(\Large y \) برابر است با \(\Large af'(x) \). برای اثبات داریم:
\(\LARGE y’=\lim\limits_{h\to 0} \frac{af(x+h)-af(x)}{h} \)
\(\LARGE =\lim\limits_{h\to 0} a\frac{f(x+h)-f(x)}{h} \)
\(\LARGE =af'(x) \)
مشتق عبارات با توانهای طبیعی
اگر \(\Large f(x)=x^n \) باشد که \(\Large n \) یک عدد طبیعی است، \(\Large f'(x) \) برابر است با \(\Large nx^{n-1} \). به طور مثال، مشتق تابع \(\Large f(x)=x^3 \) برابر است با \(\Large f'(x)=3x^2 \). برای اثبات این قضیه داریم:
\(\Large f'(x)=\lim\limits_{h\to 0} \frac{f(x+h)-f(x)}{h} \)
\(\Large =\lim\limits_{h\to 0} \frac{(x+h)^n-x^n}{h} \)
\(\Large =\lim\limits_{h\to 0} \frac{(x^n+nx^{n-1}h+\dots+h^n)-x^n}{h} \)
\(\Large =\lim\limits_{h\to 0} \frac{nx^{n-1}h+\frac{n(n-1)}{2}x^{n-2}h^2+\dots+h^n}{h} \)
\(\Large =\lim\limits_{h\to 0} \frac{h(nx^{n-1}+\dots+h^{n-1})}{h} \)
\(\Large =\lim\limits_{h\to 0} nx^{n-1}+\dots+h^{n-1} \)
\(\Large =nx^{n-1} \)
مشتق ریشهٔ n ام
مشتق تابع \(\Large f(x)=\sqrt[n]{x} \) که در آن \(\Large n \) یک عدد طبیعی است، برابر است با \(\Large f'(x)=\frac{1}{n\sqrt[n]{x^{n-1}}} \). به طور مثال مشتق تابع \(\Large f(x)=\sqrt[3]{x} \) برابر است با \(\Large f'(x)=\frac{1}{3\sqrt[3]{x^{2}}} \). برای اثبات این قضیه داریم:
\(\Large f'(x)=\lim\limits_{h\to 0} \frac{f(x+h)-f(x)}{h} \)
\(\Large =\lim\limits_{h\to 0} \frac{\sqrt[n]{x+h}-\sqrt[n]{x}}{h}= \)
\(\Large \lim\limits_{h\to 0} \frac{(\sqrt[n]{x+h}-\sqrt[n]{x})(\sqrt[n]{(x+h)^{n-1}}+\dots+\sqrt[n]{x^{n-1}})}{h(\sqrt[n]{(x+h)^{n-1}}+\dots+\sqrt[n]{x^{n-1}})} \)
\(\Large =\lim\limits_{h\to 0} \frac{(x+h)-x}{h(n\sqrt[n]{x^{n-1}})} \)
\(\Large =\lim\limits_{h\to 0} \frac{h}{h(n\sqrt[n]{x^{n-1}})} \)
\(\Large =\frac{1}{n\sqrt[n]{x^{n-1}}} \)
مشتق جمع و تفریق توابع
مشتق جمع و تفریق توابع برابر است با جمع و تفریق مشتق آنها. به زبان ساده، اگر یک عبارت جبری داشته باشیم که از جمع و تفریق چند جمله تشکیل شده باشد، کافی است ابتدا مشتق هر جمله را به دست آورده و آنها را با یکدیگر جمع و یا از یکدیگر کم کنیم. یعنی
\(\Large (f+g)'(x)=f'(x)+g'(x) \)
\(\Large (f-g)'(x)=f'(x)-g'(x) \)
مثال 3: اگر \(\Large f(x)=x^2+\sqrt[3]{x}-5 \) باشد، \(\Large f'(x) \) را بیابید.
حل: از آنجاییکه \(\Large f(x) \) را میتوان به صورت جمع و تفریق چند عبارت نوشت، کافی است مشتق هر یک از این عبارات را به دست آورده و سپس آنها را با یکدیگر جمع و یا از یکدیگر کم کنیم. اگر \(\Large g(x)=x^2 \) و \(\Large h(x)=\sqrt[3]{x} \) و \(\Large i(x)=-5 \) باشد، برای محاسبۀ \(\Large f'(x) \) داریم:
\(\LARGE g'(x)=2x \)
\(\LARGE h'(x)=\frac{1}{3\sqrt[3]{x^2}} \)
\(\LARGE i'(x)=0 \)
\(\Large f(x)=g(x)+h(x)+i(x) \)
\(\Large f'(x)=g'(x)+h'(x)+i'(x) \)
\(\Large =2x+\frac{1}{3\sqrt[3]{x^2}}+0 \)
\(\Large =2x+\frac{1}{3\sqrt[3]{x^2}} \)
مشتق ضرب توابع
مشتق ضرب تابع \(\Large f(x) \) در تابع \(\Large g(x) \) برابر است با:
\(\LARGE (fg)’=f’g+fg’ \)
به زبان ساده، مشتق ضرب دو تابع برابر است با مشتق تابع اول در تابع دوم به اضافۀ مشتق تابع دوم در تابع اول. برای اثبات داریم:
\(\Large (fg)'(x) \)
\(\Large =\lim\limits_{h\to 0} \frac{f(x+h)g(x+h)-f(x)g(x)}{h} \)
\(\Large =\lim\limits_{h\to 0} \frac{f(x+h)g(x+h)-f(x)g(x+h)}{h} \)
\(\Large +\lim\limits_{h\to 0} \frac{f(x)g(x+h)-f(x)g(x)}{h} \)
\(\Large =\lim\limits_{h\to 0} g(x+h)\frac{(f(x+h)-f(x))}{h} \)
\(\Large +\lim\limits_{h\to 0} f(x)\frac{(g(x+h)-g(x))}{h} \)
\(\Large =f'(x)g(x)+f(x)g'(x) \)
مشتق تقسیم توابع
اگر \(\Large f(x)=\frac{g(x)}{i(x)} \) باشد، \(\Large f'(x) \) طبق رابطهٔ زیر به دست میآید:
\(\LARGE f'(x)=\frac{g'(x)i(x)-i'(x)g(x)}{i^2(x)} \)
به بیان ساده تر، مشتق تقسیم دو تابع، از رابطۀ زیر به دست میآید:

اثبات این قضیه، به صورت زیر انجام میشود:
\(\Large f'(x)=\lim\limits_{h\to 0} \frac{\frac{g(x+h)}{i(x+h)}-\frac{g(x)}{i(x)}}{h} \)
\(\Large =\lim\limits_{h\to 0} \frac{g(x+h)i(x)-i(x+h)g(x)}{i(x+h)i(x)h} \)
\(\Large =\lim\limits_{h\to 0} \frac{g(x+h)i(x)-g(x)i(x)}{i(x+h)i(x)h} \)
\(\Large +\lim\limits_{h\to 0} \frac{g(x)i(x)-g(x)i(x+h)}{i(x+h)i(x)h} \)
\(\Large =\lim\limits_{h\to 0} \frac{i(x)(g(x+h)-g(x))}{i(x+h)i(x)h} \)
\(\Large +\lim\limits_{h\to 0} \frac{g(x)(i(x)-i(x+h))}{i(x+h)i(x)h} \)
\(\Large =\lim\limits_{h\to 0} \frac{i(x)(\frac{g(x+h)-g(x)}{h})}{i(x+h)i(x)} \)
\(\Large -\lim\limits_{h\to 0} \frac{g(x)(\frac{i(x+h)-i(x)}{h})}{i(x+h)i(x)} \)
\(\Large =\lim\limits_{h\to 0} \frac{i(x)g'(x)}{i^2(x)} \)
\(\Large -\lim\limits_{h\to 0} \frac{g(x)i'(x)}{i^2(x)} \)
\(\Large =\lim\limits_{h\to 0} \frac{g'(x)i(x)-g(x)i'(x)}{i^2(x)} \)
مثال از مشتق تقسیم توابع
مثال 4: اگر \(\Large f(x)=\frac{x^2+x+3}{x+1} \) باشد، \(\Large f'(x) \) را بیابید.
حل: \(\Large f(x) \) را میتوانیم به صورت \(\Large \frac{g(x)}{i(x)} \) بنویسیم که در آن \(\Large g(x) \) برابر با صورت کسر است و \(\Large i(x) \) برابر با مخرج کسر. در این صورت برای محاسبه تابع مشتق \(\Large f(x) \) داریم:
\(\LARGE g(x)=x^2+x+3 \)
\(\LARGE g'(x)=2x+1 \)
\(\LARGE i(x)=x+1 \)
\(\LARGE i'(x)=1 \)
\(\LARGE f'(x)=\frac{g'(x)i(x)-i'(x)g(x)}{i^2(x)} \)
\(\LARGE =\frac{(2x+1)(x+1)-1 \times (x^2+x+3)}{(x+1)^2} \)
\(\LARGE =\frac{x^2+2x-2}{(x+1)^2} \)
مشتق ترکیب توابع
مشتق تابع \(\Large f(g(x)) \) برابر است با:
\(\LARGE (fog)'(x)=g'(x)f'(g(x)) \)
به این قضیه، قاعده زنجیری نیز میگویند. اگر \(\Large f \) تابعی از \(\Large u \) باشد و \(\Large u \) تابعی از \(\Large x \)، می توانیم قاعده زنجیری را به صورت زیر بازنویسی کنیم:
\(\Large y=f(u) \Rightarrow y’=u’f'(u)\)
از آنجاییکه اثبات این قضیه در کتاب نیامده است، ما نیز از بیان آن صرف نظر میکنیم (اثبات این قضیه بسیار زیباست. به دوستان علاقهمند توصیه میکنیم که در مورد اثبات آن تحقیق کنند). یک حالت خاص از ترکیب توابع وجود دارد که در محاسبهٔ توابع مشتق، زیاد به کار میرود. این حالت زمانی رخ میدهد که یک جمله با توان طبیعی با تابع دیگری ترکیب شده باشد. یعنی داشته باشیم:
\(\Large y=u^n\)
که \(\Large u \) تابعی از \(\Large x \) است. در این حالت، مشتق \(\Large f \) برابر است با:
\(\Large y’=u’ \times nu^{n-1}\)
مثالهایی از مشتق ترکیب توابع
مثال 5: مشتق تابع \(\Large f(x)=(2x^2+3x-5)^4 \) را به دست آورید (نیازی به ساده کردن نیست).
حل: میتوانیم \(\Large f(x) \) را به صورت ترکیب دو تابع \(\Large g(x) \) و \(\Large h(x) \) به صورت زیر بنویسیم:
\(\LARGE g(x)=x^4 \)
\(\LARGE h(x)=2x^2+3x-5 \)
\(\LARGE f(x)=g(h(x)) \)
حال طبق قاعده زنجیری میتوانیم مشتق تابع \(\Large f(x) \) را به صورت زیر بنویسیم:
\(\LARGE f'(x)=h'(x)g'(h(x)) \)
\(\LARGE g'(x)=4x^3 \)
\(\Large g'(h(x))=4(2x^2+3x-5)^3 \)
\(\Large h'(x)=4x+3 \)
\( f'(x)=4(4x+3)(2x^2+3x-5)^3\)
مثال 6: مشتق تابع \(\Large f(x)=(\frac{x^3+3x}{x^2+2})^3 \) را به دست آورید (نیازی به ساده کردن نیست).
حل: میتوانیم \(\Large f(x) \) را به صورت ترکیب دو تابع \(\Large g(x) \) و \(\Large h(x) \) به صورت زیر بنویسیم:
\(\LARGE g(x)=x^3 \)
\(\LARGE h(x)=\frac{x^3+3x}{x^2+2} \)
\(\LARGE f(x)=g(h(x)) \)
حال طبق قاعده زنجیری میتوانیم مشتق تابع \(\Large f(x) \) را به صورت زیر بنویسیم:
\(\LARGE f'(x)=h'(x)g'(h(x)) \)
\(\LARGE g'(x)=3x^2 \)
\(\LARGE g'(h(x))=3(\frac{x^3+3x}{x^2+2})^2 \)
\(\Large h'(x)=\frac{(3x^2+3)(x^2+2)-(2x)(x^3+3x)}{(x^2+2)^2} \)
\(\LARGE h'(x)=\frac{x^4+3x^2+6}{(x^2+2)^2} \)
\(\Large f'(x)=(\frac{x^4+3x^2+6}{(x^2+2)^2})(3(\frac{x^3+3x}{x^2+2})^2 )\)
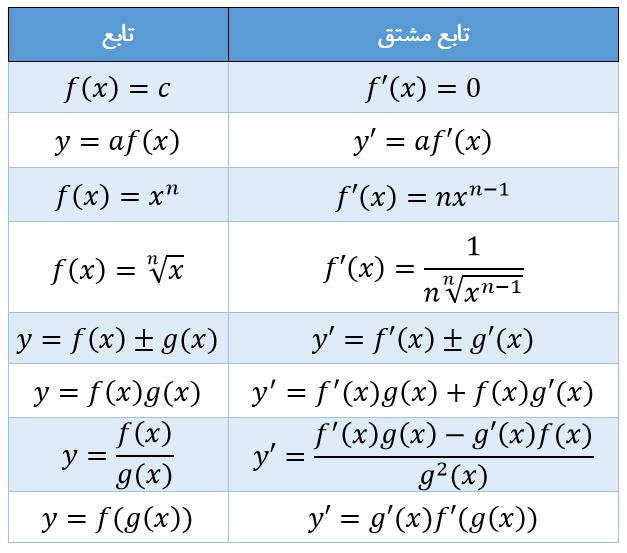
خلاصهٔ روابط مورد نیاز برای محاسبۀ مشتق توابع
در جدول زیر میتوانید تمامی روابطی را که در قسمتهای قبل نشان دادیم، به صورت یکجا ببینید.
مشتق مرتبه دوم
همان طور که گفتیم تابع مشتق \(\Large f(x) \) را با \(\Large f'(x) \) نمایش میدهیم. اگر \(\Large f'(x) \) مشتق پذیر باشد، مشتق آن را با \(\Large f”(x) \) نمایش داده و به آن مشتق مرتبه دوم میگوییم.
مثال 7: اگر \(\Large f(x)=2x^3+x^2+3x \) باشد، \(\Large f”(x) \) را به دست آورید.
حل:
\(\LARGE f'(x)=6x^2+2x+3 \)
\(\LARGE f”(x)=12x+2 \)
در ادامه مطلب پست آهنگ تغییر ریاضی دوازدهم رو مطالعه کنید.
زنگ آخر کلاس تابع مشتق
در این درسنامه تابع مشتق را معرفی کردیم. همچنین، مشتق برخی از توابع را به دست آوردیم. با به خاطر سپردن آنها میتوانیم بدون محاسبه حدی که در تعریف تابع مشتق وجود داشت، مشتق بسیاری از توابع را به دست آوریم. در انتهای درسنامه نیز، مشتق مرتبه دوم را معرفی کرده و از آن یک مثال حل کردیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث تابع مشتق دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.




