اکسترمم مطلق 📈✏️ آموزش ریاضی دوازدهم تجربی – هر آنچه نیاز دارید بدانید!

در درسنامه‌ی پیش رو، با اکسترمم مطلق آشنا خواهیم شد. با وجود شباهتی که اکسترمم مطلق به اکسترمم نسبی دارد، تفاوت‌های ظریفی نیز بین این دو هست. بعد از تعریف اکسترمم مطلق (ماکزیمم مطلق و مینیمم مطلق)، با حل مثال‌های مختلف، علاوه بر درک بهتر مفهوم، تفاوت بین اکسترمم مطلق و اکسترمم نسبی را نیز متوجه خواهیم ‌شد.

اکسترمم مطلق

اکسترمم‌های مطلق تابع نیز مانند اکسترمم‌های نسبی به دو دسته‌ٔ اصلی تقسیم می‌شوند. در ادامه هر کدام را تعریف کرده و سپس به حل چند مثال مهم خواهیم ‌پرداخت. دو دستهٔ اصلی اکسترمم مطلق عبارتند از:

1. ماکزیمم مطلق
2. مینیمم مطلق

ماکزیمم مطلق

می‌گوییم تابع \(\Large  f \) در نقطه‌ٔ \(\Large  a \) دارای ماکزیمم مطلق است، هرگاه مقدار \(\Large  f \) در نقطه‌ٔ \(\Large  x=a \) از مقدار \(\Large  f \) در هر نقطه‌ٔ دیگری از دامنه‌ی تابع بیشتر باشد. در این حالت، مقدار \(\Large  f(a) \) را نیز ماکزیمم مطلق \(\Large  f \) می‌نامیم. برای اینکه مفهوم ماکزیمم مطلق را بهتر درک کنید، نمودار تابع \(\Large  f(x) \) که در شکل زیر رسم شده است را در نظر بگیرید:

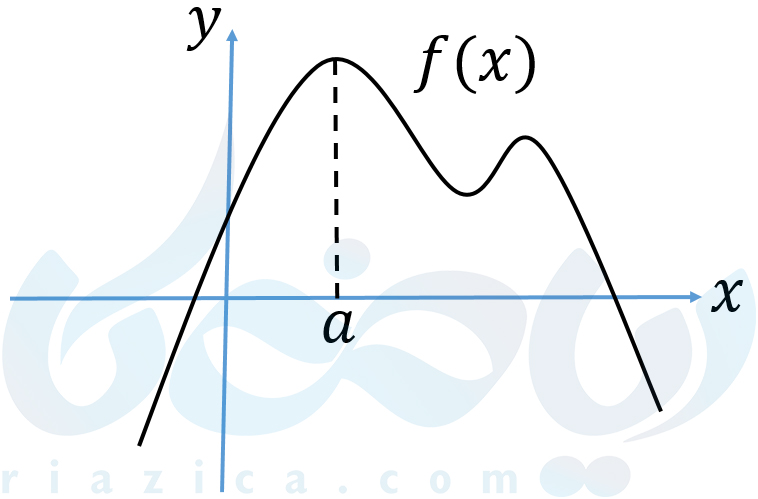
همان طور که می‌بینید، مقدار تابع \(\Large  f \) در نقطه‌ٔ \(\Large  a \) از هر نقطه‌ٔ دیگری در دامنه‌ٔ تابع بیشتر است. بنابراین، با توجه به تعریف می‌گوییم تابع \(\Large  f \) در نقطه‌ی \(\Large  a \) ماکزیمم مطلق دارد و مقدار ماکزیمم مطلق برابر است با \(\Large  f(a) \). این ماکزیمم مطلق یکی از دو اکسترمم مطلق است. در ادامه با مورد دوم آشنا می‌شویم.

مینیمم مطلق

می‌گوییم تابع \(\Large  f \) در نقطه‌ٔ \(\Large  b \) دارای مینیمم مطلق است، هرگاه مقدار \(\Large  f \) در نقطه‌ٔ \(\Large  x=b \) از مقدار \(\Large  f \) در هر نقطه‌ٔ دیگری از دامنه‌ی تابع کمتر باشد. در این حالت، مقدار \(\Large  f(b) \) را نیز مینیمم مطلق \(\Large  f \) می نامیم. برای اینکه مفهوم مینیمم مطلق را بهتر درک کنید، نمودار تابع \(\Large  f(x) \) که در شکل زیر رسم شده است را در نظر بگیرید:

همان طور که می‌بینید، مقدار تابع \(\Large  f \) در نقطه‌ی \(\Large x=b \) از هر نقطه‌ی دیگری در دامنه‌ی تابع کمتر است. بنابراین، با توجه به تعریف می‌گوییم تابع \(\Large  f \) در نقطه‌ی \(\Large  x=b \) مینیمم مطلق دارد و مقدار مینیمم مطلق برابر است با \(\Large  f(b) \).

تفاوت اکسترمم مطلق و اکسترمم نسبی

اگر تعریف ماکزیمم مطلق و مینیمم مطلق را با تعریف ماکزیمم نسبی و مینیمم نسبی مقایسه کنید، متوجه یک تفاوت بزرگ خواهید‌ شد. مقدار تابع در اکسترمم نسبی تنها در یک همسایگی بررسی می‌شود. این در حالی است که برای پیدا کردن اکسترمم مطلق باید مقدار تابع در یک نقطه‌ را با مقدار تابع در کل دامنه مقایسه کنیم. برای اینکه تفاوت این دو مفهوم روشن‌تر شود، نمودار تابع \(\Large  f(x) \) را که در شکل زیر رسم شده است، در نظر بگیرید:

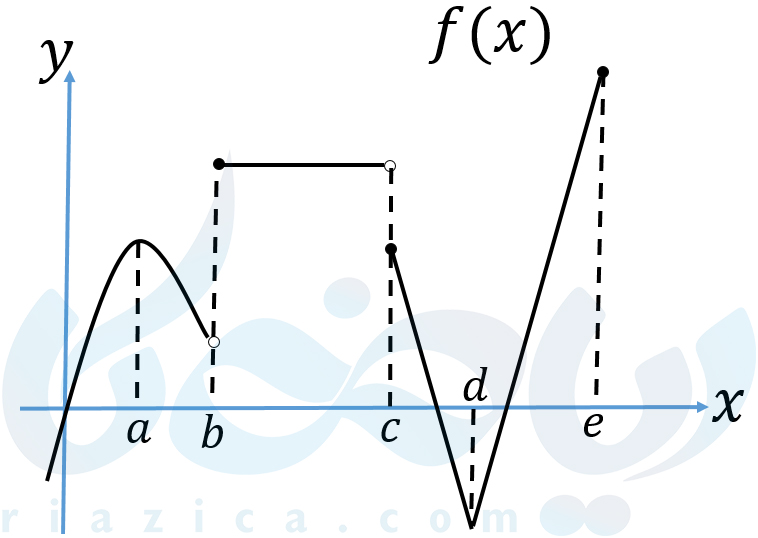
در جدول زیر وضعیت هر نقطه را مشخص کرده ایم:

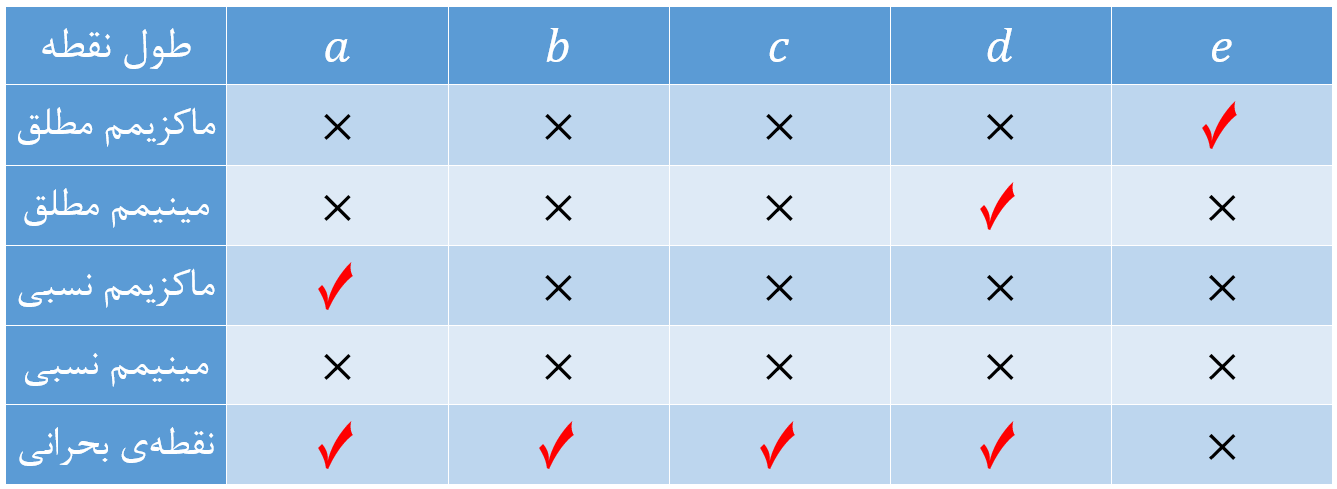
همان‌طور که در جدول بالا دیدید، تابع در نقطه‌‌ٔ \(\Large  x=a \) اکسترمم نسبی دارد اما اکسترمم مطلق ندارد. برعکس، تابع در نقاط \(\Large  x=d \) و  \(\Large  x=e \) اکسترمم مطلق دارد اما اکسترمم نسبی ندارد. بنابراین هر اکسترمم مطلقی لزوماً یک اکسترمم نسبی نیست و هر اکسترمم نسبی نیز لزوماً یک اکسترمم مطلق نیست.

اکسترمم مطلق تابع پیوسته در بازه‌ٔ بسته

زمانی که تابع در یک بازه‌ٔ بسته پیوسته باشد، در این بازه هم ماکزیمم مطلق دارد و هم مینیمم مطلق. به طور مثال، تابع \(\Large  g(x) \) در شکل زیر، در بازهٔ بستهٔ \(\Large  [a, b] \) پیوسته بوده و دارای مینیمم مطلق \(\Large  -1 \) و ماکزیمم مطلق \(\Large  2 \) است.

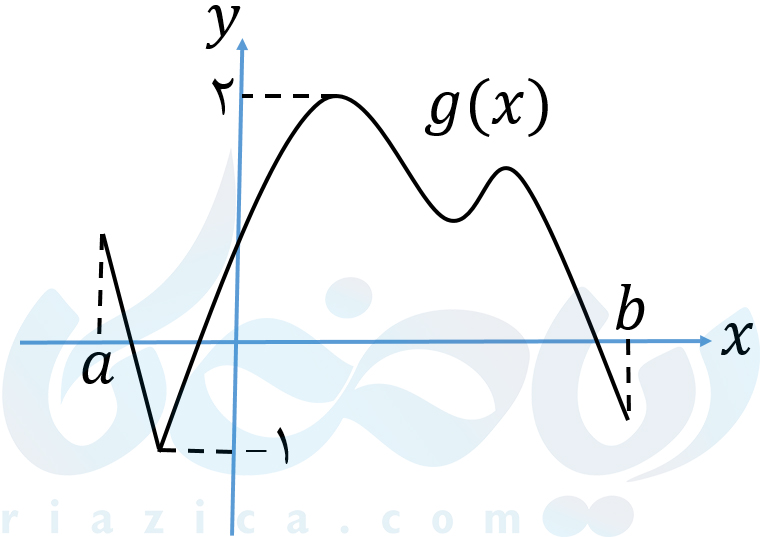
برای به دست آوردن اکسترمم های مطلق تابع پیوسته در بازه‌ٔ بسته ، ابتدا نقاط بحرانی تابع در بازه را پیدا می‌کنیم. سپس مقدار تابع در نقاط بحرانی و در دو سر بازه را به دست می‌آوریم. بزرگترین مقدار به دست آمده، ماکزیمم مطلق تابع و کوچکترین مقدار، مینیمم مطلق تابع در بازه‌ی بستهٔ مورد نظر خواهد بود. در ادامه به بررسی چند مثال مهم خواهیم پرداخت تا با نحوه‌ٔ به دست آوردن اکسترمم مطلق تابع پیوسته در بازهٔ بسته آشنا شویم.

چند مثال از اکسترمم مطلق

مثال 1: مقادیر ماکزیمم مطلق و مینیمم مطلق تابع \(\Large  f(x)=-2x^3+9x^2+4 \) در بازهٔ \(\Large  [-1, 2] \) را به دست آورید.

حل: تابع \(\Large  f \) پیوسته و بازه‌ٔ \(\Large  [-1, 2] \) بسته است. ابتدا نقاط بحرانی را به دست می‌آوریم:

\(\LARGE  f'(x)=-6x^2+18x \)

\(\LARGE  f'(x)=0 \)

\(\LARGE  \Rightarrow -6x^2+18x=0 \)

\(\LARGE  \Rightarrow x=0, 3 \)

تنها \(\Large  x=0 \) در بازه‌ی \(\Large  [-1, 2] \) قرار دارد. بنابراین کافی است مقدار تابع \(\Large  f \) در نقطه‌ٔ \(\Large  x=0 \) که نقطه‌ٔ بحرانی است و در دو سر بازهٔ \(\Large  [-1, 2] \) یعنی در نقاط \(\Large  x=-1 \) و \(\Large  x=2 \) به دست آوریم:

\(\LARGE  f(0)=4 \)

\(\LARGE  f(-1)=15 \)

\(\LARGE  f(2)=24 \)

بنابراین ماکزیمم مطلق \(\Large  f \) در بازه‌ٔ \(\Large  [-1,2] \) برابر است با \(\Large  24 \). مینیمم مطلق تابع \(\Large  f \) نیز در بازه‌ٔ \(\Large  [-1, 2] \) برابر است با \(\Large  4 \). به همین سادگی دو اکسترمم مطلق این مثال را محاسبه کردیم

مثال 2: مقادیر ماکزیمم مطلق و مینیمم مطلق تابع \(\Large  g(x)=x^3+6x+6 \) در بازهٔ \(\Large  [-2, 1] \) را به دست آورید.

حل: تابع \(\Large  g \) پیوسته و بازه‌ٔ \(\Large  [-2, 1] \) بسته است. ابتدا نقاط بحرانی را به دست می‌آوریم:

\(\LARGE  g'(x)=3x^2+6 \)

\(\LARGE  g'(x)=0 \)

\(\LARGE  \Rightarrow 3x^2+6=0 \)

\(\LARGE  \Rightarrow x^2=-2 \)

اما معادله‌ٔ بالا در مجموعه‌ی اعداد حقیقی جواب ندارد. بنابراین \(\Large  g(x) \) در بازه‌ٔ مورد نظر، فاقد نقطه‌ی بحرانی است. کافی است مقدار تابع در دو سر بازه‌ٔ \(\Large  [-2, 1] \) یعنی در نقاط \(\Large  x=-2 \) و \(\Large  x=1 \) را به دست آوریم:

\(\LARGE  g(-2)=-14 \)

\(\LARGE  g(1)=13 \)

بنابراین ماکزیمم مطلق \(\Large  g \) در بازه‌ٔ \(\Large  [-2, 1] \) برابر است با \(\Large  13 \). مینیمم مطلق تابع \(\Large  g \) نیز در بازه‌ٔ \(\Large  [-2, 1] \) برابر است با \(\Large  -14 \).

یک مثال مهم و کمی متفاوت!

مثال 3: اکسترمم های مطلق تابع \(\Large  h(x)=|x^2+3x-4| \) را در بازه‌ٔ \(\Large  [-6, 2] \) به دست آورید.

حل: تابع \(\Large  h \) پیوسته و بازه‌ٔ \(\Large  [-6, 2] \) بسته است. برای پیدا کردن اکسترمم مطلق ، ابتدا عبارت درون قدر مطلق را تعیین علامت می‌کنیم. در صورتی که چگونگی تعیین علامت یک تابع را فراموش کرده‌اید، می‌توانید به درسنامه‌ی تعیین علامت عبارت‌های جبری در آموزش پایه‌ی دهم مراجعه کنید.

باتوجه به جدول بالا، برای به دست آوردن نقاط بحرانی \(\Large  h \) در بازه‌ی \(\Large  (1, +\infty) \) یا \(\Large  (-\infty, -4) \) داریم:

\(\LARGE  h'(x)=0 \)

\(\LARGE  \Rightarrow 2x+3=0 \)

\(\LARGE  \Rightarrow x=-\frac{3}{2} \)

اما \(\Large  x=-\frac{3}{2} \) درون هیچ یک از دو بازه‌ی \(\Large  (1, +\infty) \) و \(\Large  (-\infty, -4) \) قرار ندارد.

برای به دست آوردن نقاط بحرانی \(\Large  h \)  در بازه‌ی \(\Large  (-4, 1) \) داریم:

\(\LARGE  h'(x)=0 \)

\(\LARGE  \Rightarrow -2x-3=0 \)

\(\LARGE  \Rightarrow x=-\frac{3}{2} \)

نقطه‌ٔ  \(\Large  x=-\frac{3}{2} \) درون بازه‌ٔ \(\Large  (-4, 1) \) قرار دارد، بنابراین نقطه‌ٔ بحرانی تابع است. اما باید دقت کنیم برای پیدا کردن نقاط بحرانی، علاوه بر نقاطی که دارای مشتق صفر هستند، باید به دنبال نقاطی باشیم که مشتق در آن‌ها وجود ندارد. این یک نکتهٔ مهم در درس اکسترمم مطلق است. در تابع \(\Large  h \) به دلیل وجود قدر مطلق، مشتق در نقاط \(\Large  x=1 \) و \(\Large  x=-4 \) موجود نیست، زیرا مشتق چپ و راست در این نقاط با هم برابر نیستند. مشتق راست در نقطه‌ی \(\Large  x=-4\) برابر است با:

\(\LARGE  \lim\limits_{x\to-4^+} \frac{h(x)-h(-4)}{x-(-4)}\)

\(\LARGE  =\lim\limits_{x\to-4^+} \frac{(-x^2-3x+4)-(0)}{x+4}\)

\(\LARGE  =\lim\limits_{x\to-4^+} \frac{-(x+4)(x-1)}{x+4}\)

\(\LARGE  =\lim\limits_{x\to-4^+} \frac{-(x-1)}{1}=5\)

مشتق چپ در نقطه‌ی \(\Large  x=-4\) برابر است با:

\(\LARGE  \lim\limits_{x\to-4^-} \frac{h(x)-h(-4)}{x-(-4)}\)

\(\LARGE  =\lim\limits_{x\to-4^-} \frac{(x^2+3x-4)-(0)}{x+4}\)

\(\LARGE  =\lim\limits_{x\to-4^-} \frac{(x+4)(x-1)}{x+4}\)

\(\LARGE  =\lim\limits_{x\to-4^-} \frac{(x-1)}{1}=-5\)

همان طور که دیدید، مشتق چپ و راست در نقطه‌ی \(\Large  x=-4\) برابر نیست.

در نقطه‌ٔ \(\Large  x=1 \) مشتق راست برابر است با:

\(\LARGE  \lim\limits_{x\to1^+} \frac{h(x)-h(1)}{x-1}\)

\(\LARGE  =\lim\limits_{x\to1^+} \frac{(x^2+3x-4)-(0)}{x-1}\)

\(\LARGE  =\lim\limits_{x\to1^+} \frac{(x+4)(x-1)}{x-1}\)

\(\LARGE  =\lim\limits_{x\to1^+} \frac{(x+4)}{1}=5\)

مشتق چپ در نقطه‌ٔ \(\Large  x=1\) برابر است با:

\(\LARGE  \lim\limits_{x\to1^-} \frac{h(x)-h(1)}{x-1}\)

\(\LARGE  =\lim\limits_{x\to1^-} \frac{(-x^2-3x+4)-(0)}{x-1}\)

\(\LARGE  =\lim\limits_{x\to1^-} \frac{-(x+4)(x-1)}{x-1}\)

\(\LARGE  =\lim\limits_{x\to1^-} \frac{-(x+4)}{1}=-5\)

همان طور که دیدید، مشتق چپ و راست در نقطهٔ \(\Large  x=1\) هم برابر نیست. بنابراین نقاط \(\Large  x=-4 \) و \(\Large  x=1 \) هم جزء نقاط بحرانی تابع محسوب می‌شوند. پس باید مقدار تابع \(\Large  h \) در نقاط \(\Large  x=-\frac{3}{2} \) و \(\Large  x=-4 \) و \(\Large  x=1 \) که نقاط بحرانی هستند و در دو سر بازهٔ \(\Large  [-6, 2] \) یعنی در نقاط \(\Large  x=-6 \) و \(\Large  x=2 \) به دست آوریم:

\(\LARGE  h(-\frac{3}{2})=\frac{25}{4} \)

\(\LARGE  h(-4)=0 \)

\(\LARGE  h(1)=0 \)

\(\LARGE  h(-6)=14 \)

\(\LARGE  h(2)=6 \)

بنابراین ماکزیمم مطلق \(\Large  h\) در بازه‌ٔ \(\Large  [-6, 2] \) برابر است با \(\Large  14 \). مینیمم مطلق تابع \(\Large  h \) نیز در بازه‌ی \(\Large  [-6, 2] \) برابر است با \(\Large  0 \).

توصیه می شود قبل از خوندن این پست ،پست اکسترمم نسبی ،یکنوایی،نقطه بحرانی دوازدهم را مطالعه کنید.

زنگ آخر کلاس اکسترمم مطلق

در درسنامه‌ای که با یکدیگر خواندیم، با مفهوم اکسترمم مطلق آشنا شدیم. همان طور که دیدید، بر خلاف اکسترمم نسبی، برای یافتن اکسترمم مطلق نیاز داریم تا مقدار تابع در یک نقطه را با مقدار تابع در کل دامنه مقایسه کنیم. علاوه بر این، روش به دست آوردن اکسترمم مطلق توابع پیوسته در یک بازه‌ ی بسته را با یکدیگر بررسی کردیم.

ما در ریاضیکا آماده‌ٔ هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث اکسترمم مطلق‌ پایهٔ دوازدهم تجربی دارید، در دیدگاه‌ها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند ‌داد.