آموزش ریاضی پایه هفتم
شکل های هم نهشت ریاضی هفتم 📈📉- نظیر به نظیر!
در درسنامۀ شکل های هم نهشت ریاضی هفتم بیان میکنیم که در چه صورتی دو شکل با یکدیگر مساوی (همنهشتی) هستند. همچنین، اجزای متناظر دو شکل هم نهشت (مساوی) را مشخص کرده و خواهیم گفت که این اجزا دو به دو با هم برابرند. در مثالهای مختلفی که حل خواهیم کرد، شکلهای مساوی را تشخیص داده و اجزای برابر را تعیین میکنیم. با ما تا انتهای درسنامۀ شکل های هم نهشت ریاضی هفتم همراه باشید.
چه شکلهایی هم نهشت هستند؟
اگر بتوانیم شکلی را با یک یا چند تبدیل تقارن، دوران، یا انتقال بر شکلی دیگر منطبق کنیم، آن دو شکل با یکدیگر مساوی (همنهشتی) هستند. مثلاً شکلهای \(\Large ABCD\) و \(\Large MNPQ\) در تصویر زیر با یکدیگر همنهشتی هستند.
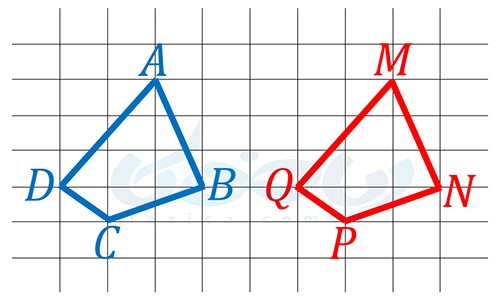
دلیل مساوی (همنهشتی) بودن دو شکل بالا این است که میتوانیم شکل \(\Large ABCD\) را با یک انتقال بر شکل \(\Large MNPQ\) منطبق کنیم. به مثال بعدی از درسنامۀ شکل های هم نهشت ریاضی هفتم دقت کنید.
مثال از شکلهای هم نهشت
مثال 1: در تصویر زیر دو مثلث \(\Large ABC\) و \(\Large MNP\) با یکدیگر هم نهشت هستند. چگونه میتوانیم با تبدیلاتی که گفتیم، این دو شکل را بر یکدیگر منطبق کنیم؟
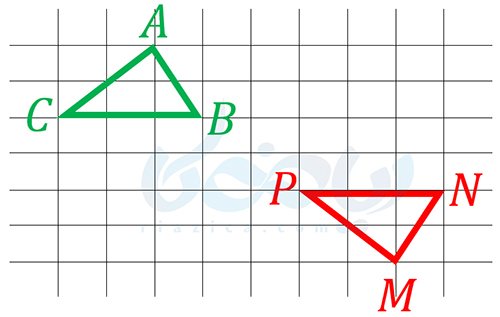
حل: کافی است مطابق تصویر زیر، ابتدا قرینۀ مثلث \(\Large ABC\) نسبت به خط \(\Large d\) را به دست آورده و سپس آن را انتقال دهیم تا بر مثلث \(\Large MNP\) منطبق شود:
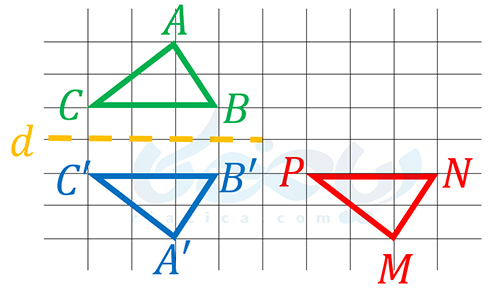
به مثال بعدی از درسنامۀ شکل های هم نهشت ریاضی هفتم دقت کنید.
مثال از ششضلعیهای هم نهشت
مثال 2: در تصویر زیر، دو ششضلعی \(\Large ABCDEF\) و \(\Large MNPQRS\) با هم هم نهشت (مساوی) هستند. به چند صورت میتوانیم تنها با یک تبدیل، ششضلعی \(\Large ABCDEF\) را بر ششضلعی \(\Large MNPQRS\) منطبق کنیم؟
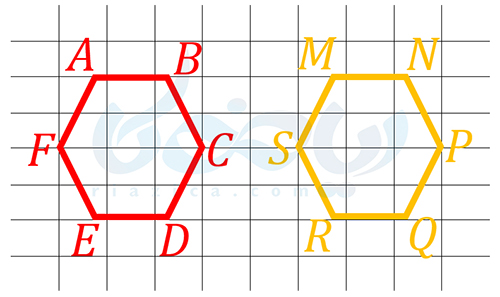
حل: هم با استفاده از تقارن، هم با استفاده از انتقال و هم با استفاده از دوران میتوانیم شکل \(\Large ABCDEF\) را بر شکل \(\Large MNPQRS\) منطبق کنیم. واضح است که طبق تصویر زیر میتوانیم با استفاده از قرینۀ شکل \(\Large ABCDEF\) نسبت به خط \(\Large d\)، شکل \(\Large ABCDEF\) را بر شکل \(\Large MNPQRS\) منطبق کنیم:
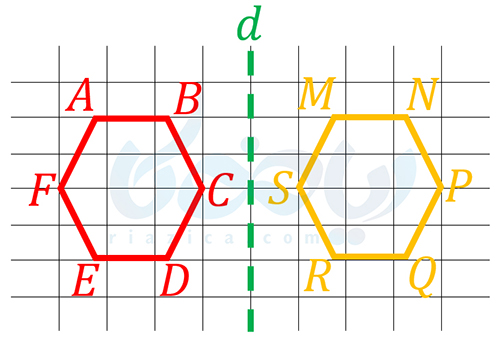
با استفاده از انتقال نیز، شکل \(\Large ABCDEF\) بر شکل \(\Large MNPQRS\) مطابق تصویر زیر منطبق میشود:
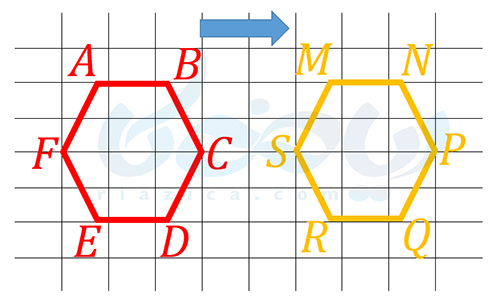
در نهایت، با استفاده از دوران \(\Large 180\) درجۀ شکل \(\Large ABCDEF\) نسبت به نقطۀ \(\Large O\)، ششضلعی \(\Large ABCDEF\) بر \(\Large MNPQRS\) مطابق تصویر زیر منطبق خواهد شد:
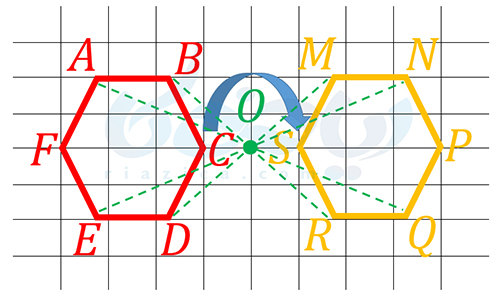
به قسمت بعدی از درسنامۀ شکل های هم نهشت ریاضی هفتم دقت کنید.
اجزای متناظر در شکل های هم نهشت ریاضی هفتم
در شکلهای هم نهست (مساوی)، اجزای متناظر دو به دو با یکدیگر برابر هستند. اما منظور از اجزای متناظر چیست؟ برای اینکه بهتر متوجه شوید، تصویر زیر را در نظر بگیرید:
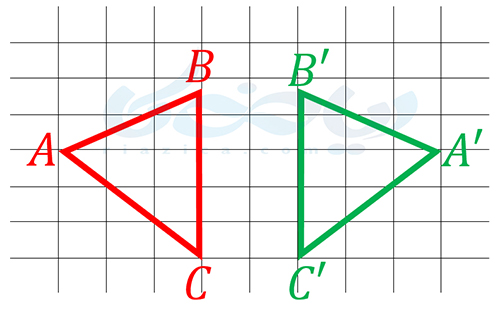
مطابق تصویر زیر، اگر قرینۀ شکل \(\Large ABC\) نسبت به خط \(\Large d\) را به دست آوریم، شکل \(\Large A’B’C’\) به دست میآید:
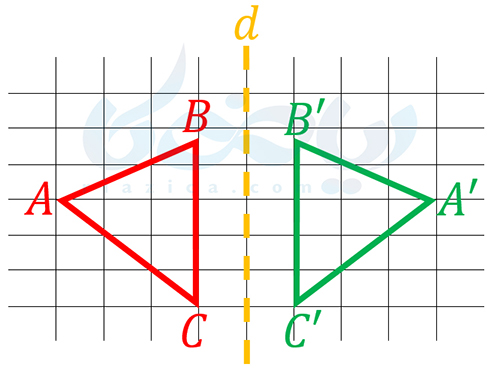
بنابراین شکلهای \(\Large ABC\) و \(\Large A’B’C’\) با یکدیگر همنهشتی (مساوی) هستند. از طرفی میبینیم که اگر شکل \(\Large ABC\) را با استفاده از تقارنی که گفتیم، بر شکل \(\Large A’B’C’\) منطبق کنیم، ضلع \(\Large AB\) روی ضلع \(\Large A’B’\)، ضلع \(\Large BC\) روی ضلع \(\Large B’C’\) و ضلع \(\Large CA\) روی ضلع \(\Large C’A’\) میافتد. بنابراین در این دو شکل، ضلع \(\Large AB\) با ضلع \(\Large A’B’\) متناظر است، ضلع \(\Large BC\) با ضلع \(\Large B’C\) متناظر است و ضلع \(\Large CA\) نیز با ضلع \(\Large C’A’\) است. در نتیجه، این اضلاع دو به دو با هم برابرند. یعنی داریم:
\(\LARGE AB=A’B’\)
\(\LARGE BC=B’C’\)
\(\LARGE CA=C’A’\)
همین موضوع برای زوایای این دو شکل از درسنامۀ شکل های هم نهشت ریاضی هفتم نیز برقرار است. یعنی وقتی شکل \(\Large ABC\) را بر شکل \(\Large A’B’C’\) منطبق میکنیم، زوایۀ \(\Large A\) بر زاویۀ \(\Large A’\)، زاویۀ \(\Large B\) بر زاویۀ \(\Large B’\) و زاویۀ \(\Large C\) بر زاویۀ \(\Large C’\) منطبق میشود. در نتیجه این زوایا دو به دو با یکدیگر متناظر و برابرند. یعنی داریم:
\(\LARGE \hat{A}=\hat{A’}\)
\(\LARGE \hat{B}=\hat{B’}\)
\(\LARGE \hat{C}=\hat{C’}\)
به این زاویه ها ،زوایای نظیر به نظبر گفته می شود.
به مثال بعدی از درسنامۀ شکل های هم نهشت ریاضی هفتم دقت کنید.
مثال از اجزای متناظر مثلثهای هم نهشت
مثال 3: در شکل زیر دو مثلث \(\Large ABC\) و \(\Large MNP\) هم نهشت هستند. تساویهای بین اضلاع و زوایای متناظر را بنویسید.
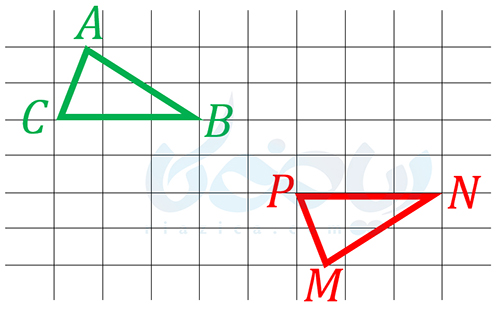
حل: مطابق شکل زیر، اگر قرینۀ مثلث \(\Large ABC\) نسبت به خط \(\Large d\) را به دست آورده و سپس آن را انتقال دهیم، مثلث \(\Large ABC\) بر مثلث \(\Large MNP\) منطبق خواهد شد:
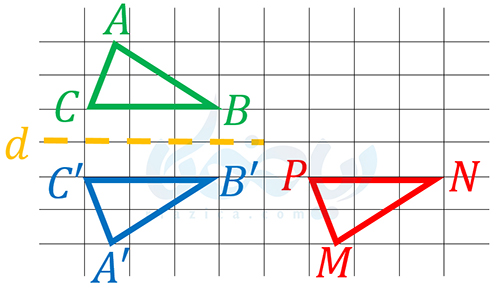
بنابراین تساویهای زیر بین اضلاع متناظر وجود دارد:
\(\LARGE AB=MN\)
\(\LARGE BC=NP\)
\(\LARGE CA=PM\)
تساوی بین زوایای متناظر نیز به صورت زیر است:
\(\LARGE \hat{A}=\hat{M}\)
\(\LARGE \hat{B}=\hat{N}\)
\(\LARGE \hat{C}=\hat{P}\)
بهتره قبل خوندن این مطلب پست تبدیلات هندسی ریاضی هفتم رو مطالعه کنید
زنگ آخر کلاس شکل های هم نهشت ریاضی هفتم
در این درسنامه از ریاضی هفتم، دیدیم که دو شکل در چه صورتی با یکدیگر همنهشتی (مساوی) هستند. نحوۀ تشخیص اجزای متناظر در دو شکل هم نهشت را بررسی کردیم. همچنین گفتیم که اجزای متناظر در شکلهای همنهشتی، دو به دو با یکدیگر مساوی هستند. سعی کردیم با بررسی مثالهای مختلف از شکلهای هم نهشت، در درک بهتر این مبحث به شما کمک کنیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث شکل های هم نهشت ریاضی هفتم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





خوب بود ممنون ♥️
سلام و عرض ادب
ممنون از توجهی که داشتید.
موفق باشید.
سلام وقت بخیر میشه درمورد زاویه نظیر به نظیر به صورت خلاصه بگید
با سلام واحترام
وفتی دو مثلث با هم همنهشت هستن مثلا زاویه ۹۰ درجه از یک مثلث با زاویه ۹۰ درجه از مثلث دیگر برابر است واصلاع روبروی ابن زاویه ها هم با هم زاویه ۶۰ درجه از یک مثلث با زاویه ۶۰ درجه از مثلث دیگر
عالی هستید ممنونم
جوابم رو نگرفتم
با سلام
چرا؟
خیلی خوب بود مرصی?
با سلام وعرض ادب
ممنون از لطف وتوجه شما دوست عزیز
با سلام واحترام
ممنون دوست عزیز
سلام وقت بخیر.
اگر در دو چهارضلعی اضلاع متناظر دو به دو باهم برابر باشند، آن دو شکل با هم هم نهشت هستند یا خیر؟
ممنون میشم جواب بدید.
با سلام و وقت به خیر
خیر همنهشت نیستند چون زاویه ها هم باید نظیر به نظیربرابر باشند
مرصینه مرسی
مرسی واقعا عالی بود (≚ᄌ≚)ℒℴѵℯ❤ ♡⃛ɞ(ू•ᴗ•ू❁)
با سلام وادب
ممنون از نگاه پر انرژی شما
نظیر به چه معناس؟
با سلام
مثلا اگه ضلعی در یکی از مثلثها در نظر میگیرید ضلعی هم موقعیت همون در مثلث دیگه باید در نظر گرفته بشه
نظیریعنی: مانند ، همانند، اینکه دو شی یا دو خط یا دوشکل و… دارای ویژگی و صفات وخصوصیات(وزن،اندازه، حجم،طول وعرض ، ارتفاع و…) یکسان داشته باشند. مثلا طول اضلاع دو مثلث با زاویه های هردو مثلث وقتی بر هم منطبق میشوند با هم یکی باشد ، کم وزیاد نباشد . وهرضلع وزاویه در مثلثی به شرط رعایت قرینه دو به دو با هر ضلع و زاویه از مثلثی دیگر برابر برابر باشند .
سلام دوست عزیز ممنون از پاسخگویی شما
ممنون از توجه شما
دو ضلع را نظیر به نظیر می گوییم که اندازه ی برابر ، جهت و راستای یکسان داشته باشند.
دو زاویه را نیز نظیر به نظیر می گوییم که اندازه برابر داشته و اضلاع شان در جهت و راستای یکدیگر باشند.
اما باید به این نکات هم دقت داشت که اولاً اجزای نظیر به نظیر فقط در شکل های هم نهشت(مساوی) وجود دارد ، ثانیاً اگر َAَBَCمثلث = ABCمثلث باشد ضلع AB با َAَB برابر است نه با َBَA اما چون ضلع جهت ندارد این اشتباه نادیده گرفته می شود
با سلام وادب ممنون از پاسخگویی شما
البته اگر دو شکل با یکی از تبدیلات هندسی (انتقال ، تقارن و دوران) بر هم منطبق شوند هم نهشت می شوند حال در ذهن اجزای نظیر به نظیر را با توجه به مفهوم بالا پیدا می کنیم.
یعنی در حالت عادی قبل از انطباق در ذهن اجزای متناظر ممکن است هم راستا نباشند(دقت کنید)
خوب بود
من امتحان نوبت اول دارمامروز.یک مشکل هست اینه که قاطی میکنیم این همنهشت هارو مشکل اینجاست
☘فصل ریاضی سخته