آموزش ریاضی پایه یازدهم تجربی
رسم نمودار تابع جز صحیح ✏️⚙️ – پله پله رسمش کن!
رسم نمودار توابع دید بهتری از تابع به ما میدهد و تفسیر و درک اطلاعات مربوط به تابع را آسانتر میکند. بنابر همین موضوع در این درسنامه نحوه رسم نمودار تابع جز صحیح را به شما اموزش خواهیم داد.
آموزش رسم نمودار تابع جزء صحیح
برای رسم نمودار تابع جز صحیح در دامنه \( \Large \mathbb{R} \) یک بازه کوچک انتخاب میکنیم و این بازه کوچک را به بازههای واحد میشکنیم و مقدار تابع را در این بازههای واحد پیدا کرده سپس نمودار را رسم کرده. به مثال زیر دقت کنید:
مثال ۱: نمودار تابع جزء صحیح \( \Large y=[ x ] \) را در بازه \( \Large (-2,2) \) رسم کنید.
حل ۱:
\( \LARGE -2 < x < -1 \rightarrow y=-2 \)
\( \LARGE -1 \leq x < 0 \rightarrow y=-1 \)
\( \LARGE 0 \leq x < 1 \rightarrow y=0 \)
\( \LARGE 1 \leq x < 2 \rightarrow y=1 \)
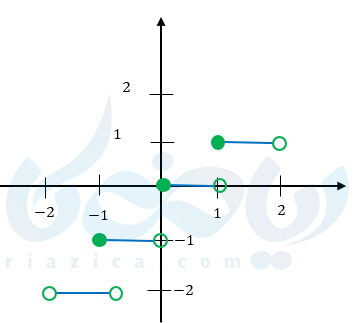
همانطور که میبینید نمودار آن یک نمودار منفصل و پلهای است برای همین به تابع جز صحیح، تابع پلهای نیز میگویند.
نکته: اگر نمودار این تابع در کل دامنه بخواهیم باز خودتان بازه مثل بازه بالا را انتخاب کرده و آن را رسم میکنیم سپس یادآور میشویم که نمودار به همین ترتیب ادامه خواهد داشت.
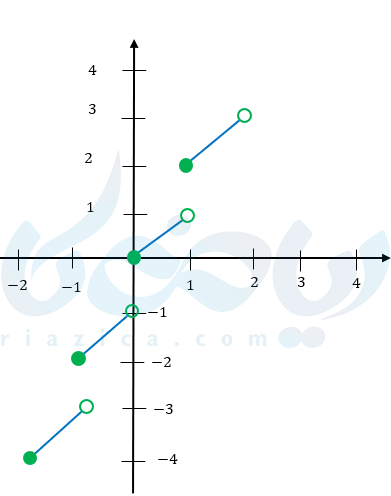
مثال ۲: نمودار تابع جزء صحیح \( \Large y=[ x ] + 1 \) را در بازه \( \Large [-3,3] \) رسم کنید.
حل ۲:
\( \LARGE -3 \leq x < -2 \rightarrow y=-2 \)
\( \LARGE -2 \leq x < -1 \rightarrow y=-1 \)
\( \LARGE -1 \leq x < 0 \rightarrow y=0 \)
\( \LARGE 0 \leq x < 1 \rightarrow y=0 \)
\( \LARGE 1 \leq x < 2 \rightarrow y=2 \)
\( \LARGE 2 \leq x < 3 \rightarrow y=3 \)
\( \LARGE x=3 \rightarrow y=4 \)
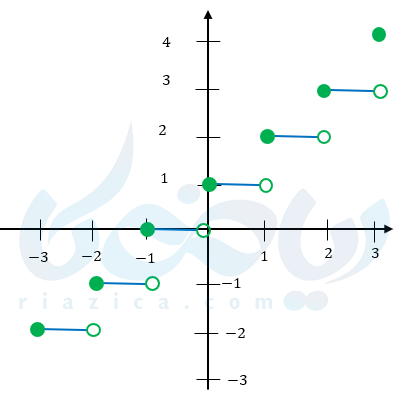
همانطور که میبینید نمودار نسبت به مثال قبل یک پله به بالا انتقال پیدا کرد.
تذکر: دقت کنید که در هر بازه ما قسمتی از یک خط (پاره خط) را داریم که با توجه به علامت \( \Large \leq \) یا \( \Large \geq \) و \( \Large < \) و \( \Large > \) ابتدا و انتهای پاره خط توپر یا توخالی خواهد بود اگر بازه اصلی به صورت \( \Large (a,b) \) باشد پاره خط ابتدایی دو طرفش خالی است ولی اگر به صورت \( \Large [a,b) \) یا \( \Large [a,b] \) باشد پاره خط ابتدایی نیز ابتدایش توپر میباشد. و در بازههای \( \Large [a,b] \) در آخر یک نقطه تکی خواهیم داشت.
مثال ۳: نمودار تابع جز صحیح \( \Large y=[2 x ] – 1 \) را رسم کنید.
حل ۳:
در این مثال برای رسم نمودار تابع جزء صحیح دامنه \( \Large \mathbb{R} \) است ولی برای رسم ما خودمان آن را در بازه \( \Large [-2,2) \) رسم میکنیم ولی یادآور میشویم که نمودار از دو طرف به همین ترتیب ادامه خواهد داشت.
نکته دیگری که در این مثال وجود دارد این است که چون ضریب \( \Large x \) را نمیتوان از براکت بیرون آورد و ما به دنبال جز صحیح
\( \Large 2x \) هستیم. \( \Large 2x \) در بازهی واحد پیدا میکنیم سپس وقتی مقدار \( \Large y \) را پیدا کردیم طول بازه را به 2 تقسیم میکنیم تا طول \( \Large x \) را بیابیم.
\( \LARGE -2 \leq 2x < -1 \)
\( \LARGE \rightarrow -1 \leq x < -\frac{1}{2} \)
\( \LARGE y=-2-1=-3 \)
\( \LARGE -1 \leq 2x < 0 \rightarrow -\frac{1}{2} \leq x <0 \)
\( \LARGE y=-1-1=-2 \)
\( \LARGE 0 \leq 2x < 1 \rightarrow 0 \leq x < \frac{1}{2} \)
\( \LARGE y=0-1=-1 \)
\( \LARGE 1 \leq 2x < 2 \rightarrow \frac{1}{2} \leq x < 1 \)
\( \LARGE y=1-1=0 \)
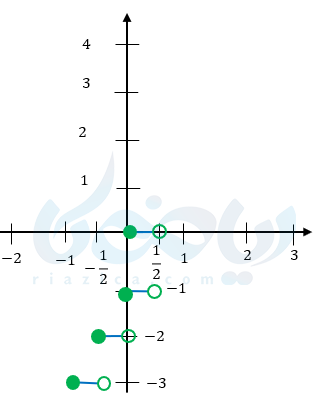
همانطور که میبینید طول پاره خطها نصف شده است یعنی ضریب باعث میشود طول پاره خطها کوتاهتر شود.
مثال ۴: نمودار تابع جز صحیح \( \Large y=[ \frac{1}{2}x ] \) را رسم کنید.
حل ۴:
در این مثال برای رسم نمودار تابع جز صحیح نیز مانند مثال قبل \( \Large [ \frac{1}{2}x ] \) را در یک بازه دلخواه \( \Large [-2,2) \) پیدا کرده سپس طول بازه را در ۲ ضرب میکنیم تا طول بازه در \( \Large x \) بدست آید.
\( \LARGE -2 \leq \frac{1}{2}x < -1 \)
\( \LARGE \rightarrow -4 \leq x < -2 \)
\( \LARGE y=-2 \)
\( \LARGE -1 \leq \frac{1}{2}x < 0 \rightarrow -2 \leq x < 0 \)
\( \LARGE y=-1 \)
\( \LARGE 0 \leq \frac{1}{2}x < 1 \rightarrow 0 \leq x < 2 \)
\( \LARGE y=0 \)
\( \LARGE 1 \leq \frac{1}{2}x < 2 \rightarrow 2 \leq x < 4 \)
\( \LARGE y=1 \)
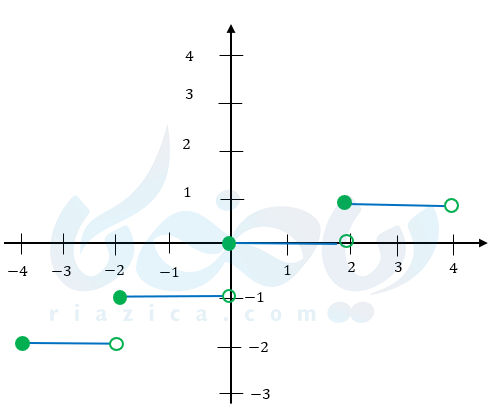
همانطور که میبینید در این مواقع طول پاره خطها بلندتر از یک واحد خواهد شد.
مثال ۵: نمودار تابع جزء صحیح \( \Large y= x + [ x ] \) را رسم کنید.
حل ۵:
در این مثال برای رسم نمودار تابع جز صحیح ابتدا مقدار \( \Large [ x ] \) را در چند بازه پیدا میکنیم سپس خطهای به دست آمده در هر بازه را با توجه به طول بازه رسم میکنیم.
\( \LARGE -2 \leq x < -1 \rightarrow y=x-2 \)
\( \LARGE -1 \leq x < 0 \rightarrow y=x-1 \)
\( \LARGE 0 \leq x < 1 \rightarrow y=x \)
\( \LARGE 1 \leq x < 2 \rightarrow y=x+1 \)
ویدیویی از رسم نمودار تابع جز صحیح
در این ویدیو آموزشی از رسم نمودار تابع جز صحیح را مشاهده میکنید.
زنگ آخر رسم نمودار تابع جز صحیح
دوستان همیشگی ریاضیکا مبحث رسم نمودار تابع جز صحیح ریاضی یازدهم تجربی را با هم یادگرفتیم. همیشه بازهها را مشخص کنید و نقطهها را بیابید. حواستان به توپر و توخالی بودن ابتدا و آخر بازه باشد.
هر سوالی که از این مبحث داشتید میتوانید در قسمت دیدگاه برایمان بنویسید. کارشناسان ریاضیکا حتما به سوالاتتان پاسخ میدهند.





سلام ببخشید 2ایکس+جزو صحیح ایکس چه طور رسم میشه
سلام و عرض ادب
ابتدا جز صحیح را در بازه های واحد مقدارش را پیدا کنید سپس معادله خطی را که بدست می آید را رسم کنید.
موفق باشید.
با تشکر از استاد موسوی
با سلام وادب
ممنون دوست عزیز
مانند مثال ۵ رسم کنید.
سلام ووقت بخیر
ببخشیدنمودارایکس در جزصحیح ایکس چطور رسم میشه؟
پاسخ داده شد
سلام ببخشید چطور میشه یجا نموداری که برای جزصحیح کشیده شده حالت خط صاف داره و یجا حالت اریب؟
در حالت پنج
چجوری باید تشخصیص بدیم؟
سلام دوست عزیز
وقتی Xای داشته باشیم که داخل براکت نیست ابتدا X داخل براکت را در بازه های متلف مشخص میکنیم سپس خظهای بدست آمده را رسم میکنیم کامل در مثال ۵ توضیح داده شده
سلام
براکت x²
رو میشه رسم کنید
ضمن عرض سلام
امشب پست اینستاگرام پیج ما رو ببینید. پاسخ سوال شما را خواهیم داد
https://www.instagram.com/riazica/
جز صحیح منفیxچطوری رسم میشه.چه فرقی باجزصحیحxداره؟کاش ی مثال اینجوری حل میکردین?
با سلام نمودار تابع جز صحیح ایکس منهای ایکس در بازه -۲ تا ۲ چجوری رسم میشه
همه بازه هاش مقدار تابع صفر میشود؟؟
بارسلام وادب
خیر در هر بازه مقدار جز صحیح رو مشخص کنید به معادله یک خخطبدست میاد که با توجه به بازه موردنظر یک نیم خط رسم میشود
مقدار دامنه رو که تعیین میکنیم برای دامنه ایکس مقادیر منفی به دست میاد توی تک واحد ها
سلام
ایکس ضربدر جز صحیح ایکس رسمش چه گونه هست
با سلام وعرض ادب
مانند مثال ۵ ابتداد مقدار جز صحیح x رو به دست آورید بعد خطهای بدست امده در بازه های مختلف را با توجه به حدود بازه ها رسم کنید
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
براکت x²
رو میشه رسم کنید
ضمن عرض سلام
امشب پست اینستاگرام پیج ما رو ببینید. پاسخ سوال شما را خواهیم داد
https://www.instagram.com/riazica/
سلام.منفی براکت x چجور رسم میشه؟
با سلام وعرض ادب
نمودار براکت x رو رسم کنید قرینه اون نسبت به محور xها رو بکشید
سوال ۳و۴ رو اشتباه حل کردید
با سلام وادب
کجای مسئله ها غلط هست؟
سلام. میشه طریقهٔ رسم نمودار [x] – x رو توضیح بدید
با سلام وعرض ادب
ابتدا براکت منفی ایکس رو در بازه های مختلف حساب کنید ومقدارش رو در ایکس ضرب کنید وبعد پاره خطها رو در بازهای مورد نظر رسم کنید
اینجا که نمیشه
سلام
چطور در هر بازه ای حتی اعشاری میش رسم کرد تابع رو ؟
کافیه شما یه بازه مثلا بین منفی سه وسه در نظر بگیرید بعد اون بازه رو به بازهای یک واحدی بشکونید ودر هر بازه مقدار جز صحیح رو مشخص کنید
سلام
تابع x بر روی جز صحیح x
و برعکس رو چطور میشه رسم کرد؟
با عرض سلام و ادب..
تابع x[x] چطوری رسم میشه؟؟
سلام و خیلی ممنون از توضیحاتتون. میخواستم بپرسم نمودار 2x-[2x] چه فرقی با نمودار x-[x] داره؟
سلام چه زمانی از روش سایه اندازی توی رسم تابع براکت استفاده میکنیم؟
با سلام وادب
در همه موارد میشه وای ما بیشتر در جایی که داخل براکت تابعی داریم که یه نمودارش به شکل منحنی هست استفاده میکنیم
سلام ببخشيد تابع جز صحيح ايكس به توان دو رو چگونه رسم كنم بازه ها شو چه طور بايد معين كنم اگر سوال گفته باشه ايكس بين منفي 2 و دو باشه
با سلام وادب
ابتدا نمودا ایکس به توان دو که سهمی هست رسم می کنیم سپس به روش سایه اندازی در محدوده خواسته شده سایه نمودار رو بر روی خط وای مساوی صفر ووای مساوی یک وغیره پیدا میکنیم
مثال سه بین بازه یک دوم تا یک را اشتباه حل کرده اید
سلام خسته نباشید
ببخشید میشه نمودار [x_2)[x^2_2x) را در بازه ی (۰و۳) رسم کنید
سلام وقتتون بخیر
ببخشید میشه دامنه تابع جز صحیح هم توضیح بدین ممنون میشم
سلام ببخشید نمودار جز صحیح ایکس بعلاوه ایکس چی میشه
سلام وقت بخیر من یه سوال داشتم
ما گفتیم که
اگر k عضو اعداد صحیح یا همون Z باشه و داشته باشیم [x + k] اون وقت میتونیم k رو از داخل براکت بکشیم بیرون و عبارت قبلی رو به این صورت بنویسیم : [x] + k . حالا من سوالم اینه که اگر k عضو اعداد صحیح نبود و داخل براکت بود چجوری باید اون براکت رو روی نمودار رسم کنیم اگر مثلا یه بازه هم بهمون داده باشن
مثلاً این طوری : [x + 1/5] این رو توی بازهی [۴,2-] اگه بخواین رسم کنیم چجوری میشه؟
سلام وقت بخیر.
نمودار تابع براکت یک به روی ایکس چجوری رسم میشه ؟ میشه کامل توضیح بدید ممنون میشم
سلام تابع جز صحیح ا به روی xچطور رسم میشه ؟
نمودار جز صحیح[1/x] 1به روی x
لطفا رسم تابعی ک هم براکت داشته باشد و هم قدر مطلق رو توضیح دهید
با سلام انشاالله در آینده نزدیک
با عرض سلام و ادب..
تابعx[x] چطوری رسم میشه؟؟
مرسی خیلی خوب بود من از این مبحث خیلی چیزا یاد گرفتم
با سلام
خدا رو شکر که مفید واقع شده
عالی توضیح دادید
با سلام ممنون از نگاه شما
سلام اگر گفته باشه y برابر با x منهای براکت x بازه رو هم مشخص کرده باشه چی
با سلام ویدیو آخر درسنامه رو نگاه کنید به جوابتون میرسید
ضمن تشکر، به عنوان یک دانش آموخته ریاضی که سال ها تدریس کردم، میخوام یک توضیح تکمیلی درمورد رسم توابع جزصحیح وقتی که داخل براکت ضریب داره بدم. به عنوان مثال y=[2x] وقتی x در بازه (2,2-] هست، پس 2x در بازه ۴- و ۴ هست و چون جز صحیح باید یک گام یک گام حرکت کند مثلاً قسمت اول ۲x را بین ۴- و ۳- در نظر می گیریم که بازه x بین ۲- و ۳٫۲- به دست میاد و الی آخر. در نهایت باید تابعی که رسم میکنیم در بازه داده شده ۲- و ۲ باشد که در پاسخ داده شده این طور نیست و طبق بازه دلخواه بخشی از نمودار ترسیم نشده (بین ۱- و ۱ نمودار ترسیم شده).
مواردی که گفتم بحث تشریحی موضوع هست و البته تو بحث تستی مراحل سریع تر میشه. تو نمودار یک دوم ایکس هم مشابه همین، نمودار تابع کامل نیست.
با سلام ممنون از توضیحات شما
سلام امکان دارد تابع [x-]+[x]=y و رسم نمودار آن را توضیح دهید.
با سلام ویدیو آخر رو ببینید
سلام میشه لطفاً سوال من رو هم جواب بدین
سلام تابع y=2[x] چطور رسم میشه؟
با سلام
مثل نمودار براکت ایکس هست فقط مقادیر در دو ضرب میشه