آموزش ریاضی پایه نهم
حجم و مساحت کره ریاضی نهم 🏐🌀 – سریع محاسبه کن!
در درسنامهٔ حجم و مساحت کره ریاضی نهم ابتدا تعریف هندسی دایره و کره را مرور میکنیم. سپس به چگونگی محاسبهٔ حجم و مساحت کره پرداخته و از آن مثال حل خواهیم کرد. با ما تا انتهای درسنامه همراه باشید.
تعریف دایره و کره
تعریف دایره: دایره، مجموعهٔ نقاطی از صفحه است که از یک نقطهٔ مشخص در آن صفحه، به یک فاصله هستند. به آن نقطهٔ مشخص، مرکز دایره و به فاصلهٔ نقاط دایره از مرکز، شعاع میگوییم.
اگر در تعریف بالا، به جای در نظر گرفتن نقاطی از صفحه، نقاطی از فضا را در نظر بگیریم، تعریف کره به دست میآید:
تعریف کره: کره، مجموعهٔ نقاطی از فضا است که از یک نقطهٔ مشخص، به یک فاصله هستند. به آن نقطهٔ مشخص، مرکز کره و به فاصلهٔ نقاط کره از مرکز آن، شعاع کره میگوییم.
در شکل زیر میتوانید کرهای به مرکز \(\Large O\) و شعاع \(\Large R\) را مشاهده کنید:
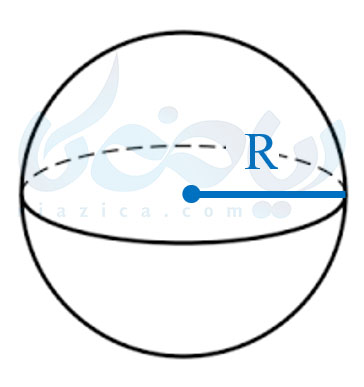
مانند دیگر اشکل هندسی، سوالی که در مورد کره به ذهنمان میرسد، چگونگی محاسبهٔ حجم و مساحت کره است. در قسمتهای بعدی از درسنامهٔ حجم و مساحت کره ریاضی نهم به این دو مطلب میپردازیم.
حجم کره ریاضی نهم
اگر کرهای به شعاع \(\Large R\) داشته باشیم، حجم آن که با \(\Large V\) نشان میدهیم، از طریق رابطهٔ زیر به دست میآید:

اثبات این که چرا حجم کره به صورت بالا به دست میآید را میتوان به دو روش زیر انجام داد:
- روش ارشمیدس و استفاده از قضیهٔ کاوالیری
- انتگرال گیری
قبل از پایه گذاری حسابان، حجم کره با استفاده از روش ارشمیدس محاسبه شد. اما بعد از آن، حجم کره با استفاده از انتگرال به سادگی به دست میآید. در کتاب درسی سعی شده روش ارشمیدس به اجمال بیان شود. ما نیز آن را به اجمال در قسمت بعدی از درسنامهٔ حجم و مساحت کره ریاضی نهم بیان خواهیم کرد. در صورتی که علاقهمندید میتوانید هم در مورد قضیهٔ کاوالیری و هم در مورد انتگرال مطالعه کنید.
اثبات رابطهٔ حجم کره
به شکل زیر نکاه کنید:
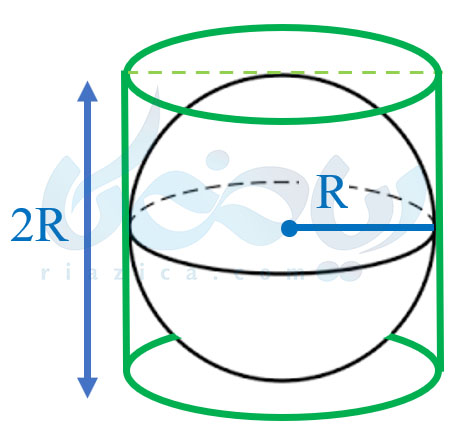
در شکل بالا، شعاع کره برابر با \(\Large R\) و ارتفاع استوانهٔ قائم برابر با دو برابر شعاع کره، یعنی \(\Large 2R\) است. همان طور که میبینید، استوانه در چهار نقطه بر کره مماس شده است. اصطلاحاً میگوییم کره در استوانه محاط شده یا به عبارت دیگر، استوانه بر کره محیط شده است. ارشمیدس ثابت کرد حجم کرهٔ بالا، دو برابر حجم فضای بین کره و استوانه است. به بیان دیگر، در شکل بالا، حجم کره، \(\Large \frac{2}{3}\) حجم استوانه است. در درسنامهٔ حجم و سطح ریاضی هفتم خواندیم که حجم استوانه برابر است با مساحت قاعدهٔ آن ضرب در ارتفاع. مساحت قاعدهٔ استوانهٔ شکل قبل برابر است با \(\Large \pi R^2\) و ارتفاع آن برابر است با دو برابر با شعاع کره، یعنی \(\Large h=2R\). بنابراین اگر حجم استوانه را با \(\Large V_c\) نشان دهیم، داریم:
\(\LARGE V_c=\pi R^2h\)
\(\LARGE =\pi R^2 \times 2R\)
\(\LARGE =2\pi R^3\)
حال حجم استوانه را داریم. از طرفی همان طور که گفتیم حجم کره برابر است با \(\Large \frac{2}{3}\) حجم استوانه. بنابراین اگر حجم کره را با \(\Large V_s\) نشان دهیم، داریم:
\(\LARGE V_s=\frac{2}{3}V_c\)
\(\LARGE =\frac{2}{3} \times 2\pi R^3\)
\(\LARGE =\frac{4}{3} \pi R^3\)
پس، حجم کره از رابطهٔ زیر به دست میآید:
\(\LARGE V=\frac{4}{3} \pi R^3\)
به مثالهای بعدی از درسنامهٔ حجم و مساحت کره ریاضی نهم توجه کنید.
مثال محاسبهٔ حجم کره ریاضی نهم
مثال 1: حجم کرهای با قطر \(\Large 6\) را محاسبه کنید (برای سادگی، \(\Large \pi\) را برابر با \(\Large 3\) در نظر بگیرید).
حل: همان طور که دیدیم، حجم کره از رابطهٔ \(\Large V=\frac{4}{3} \pi R^3\) به دست میآید. قطر کره برابر با \(\Large 6\) است. پس، شعاع آن برابر با \(\Large 3\) است. بنابراین داریم:
\(\LARGE V=\frac{4}{3} \pi R^3\)
\(\LARGE =\frac{4}{3} \times 3 \times 3^3\)
\(\LARGE =108\)
مثال محاسبهٔ حجم کره ریاضی نهم
مثال 2: آب درون یک کاسه که به شکل نیمکره است را درون استوانهای خالی میکنیم. اگر شعاع نیم کره برابر با \(\Large 3\) سانتیمتر و شعاع استوانه برابر با \(\Large 2\) سانتیمتر باشد، آب درون استوانه تا چه ارتفاعی بالا میآید؟
حل: برای حل این مسئله باید ابتدا حجم آب درون کاسه (نیمکره) را به دست آوریم. با توجه به اینکه حجم یک کره از رابطهٔ \(\Large V=\frac{4}{3} \pi R^3\) به دست میآید، حجم آب درون کاسه (\(\Large V_b\)) به صورت زیر به دست میآید:
\(\LARGE V_b=\frac{1}{2} \times \frac{4}{3} \pi R^3\)
\(\LARGE =\frac{1}{2} \times \frac{4}{3} \times \pi \times 3^3\)
\(\LARGE =18 \pi \)
این مقدار از حجم آب را درون استوانه میریزیم. فرض میکنیم در استوانه، آب تا ارتفاع \(\Large h\) بالا میآید. میخواهیم \(\Large h\) را به دست آوریم. برای این کار، باید حجم آب درون استوانه را برابر با \(\Large 18 \pi\) که همان حجم آب درون کاسه بود، قرار دهیم. ابتدا حجم آب درون استوانه (\(\Large V_c\)) را به دست میآوریم:
\(\LARGE V_c=\pi R^2 h\)
\(\LARGE =\pi \times 4 \times h\)
\(\LARGE =4 \pi h\)
اگر حجم آب درون استوانه را با حجم آب درون کره برابر قرار دهیم، مقدار \(\Large h\) به دست می آید:
\(\LARGE 18 \pi=4 \pi h\)
اگر از دو طرف، \(\Large \pi\) را ساده کنیم، داریم:
\(\LARGE 18 =4h\)
\(\LARGE \Rightarrow h=\frac{18}{4}=\frac{9}{2}\)
مساحت کره ریاضی نهم
اگر کرهای به شعاع \(\Large R\) داشته باشیم، مساحت آن که با \(\Large S\) نشان میدهیم، از طریق رابطهٔ زیر به دست میآید:

اثبات رابطهٔ مساحت کره
مساحت کره را نیز، هم میتوان به سادگی و با استفاده از انتگرال و هم بدون استفاده از انتگرال به دست آورد. در اینجا سعی میکنیم صرفاً یک آشنایی ابتدایی با روش اثبات بدون انتگرال پیدا کنیم. مجدداً یک کره را در یک استوانه محاط میکنیم:

می توان ثابت کرد که از تصویر کره، سطح جانبی استوانه به دست میآید. برای اینکه بهتر متوجه شوید، به تصویر متحرک زیر دقت کنید:

بنابراین میتوان ثابت کرد که مساحت کره برابر است با مساحت جانبی استوانه. روش به دست آوردن مساحت جانبی استوانه را در درسنامهٔ مساحت جانبی و کل ریاضی هفتم خواندیم. مساحت جانبی استوانهٔ شکل قبل برابر است با حاصل ضرب محیط قاعده استوانه که برابر است با \(\Large 2 \pi R\) در ارتفاع استوانه که برابر است با \(\Large 2R\). بنابراین اگر مساحت جانبی استوانه را با \(\Large V_c\) نشان دهیم، داریم:
\(\LARGE V_c=2 \pi R \times 2R\)
\(\LARGE =4 \pi R^2\)
همان طور که گفتیم، مساحت کره برابر است با مساحت جانبی استوانه. بنابراین مساحت کره نیز برابر است با \(\Large 4 \pi R^2\). یعنی:
\(\LARGE S=4 \pi R^2\)
مثال از مساحت کره ریاضی نهم
مثال 3: مساحت کرهای با قطر \(\Large 4\) را محاسبه کنید (برای سادگی، \(\Large \pi\) را برابر با \(\Large 3\) در نظر بگیرید).
حل: همان طور که دیدیم، مساحت کره از رابطهٔ \(\LARGE S=4 \pi R^2\) به دست میآید. قطر کره برابر با \(\Large 4\) است. پس، شعاع آن برابر با \(\Large 2\) است. بنابراین داریم:
\(\LARGE S=4 \pi R^2\)
\(\LARGE =4 \times 3 \times 2^2\)
\(\LARGE =48\)
مثال از مساحت کره ریاضی نهم
مثال 4: مساحت شکل زیر را به دست آورید (مقدار \(\LARGE \pi \) را برابر با \(\LARGE 3\) در نظر بگیرید).
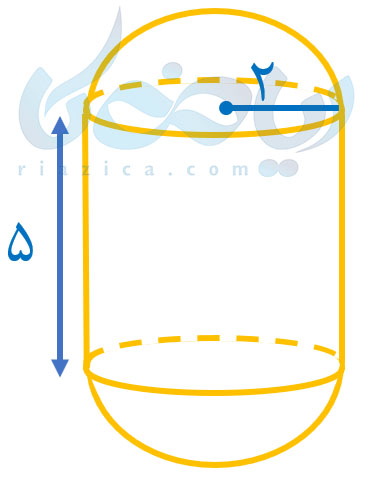
حل: همان طور که میبینید، شکل بالا از یک استوانه و دو نیم کره تشکیل شده است. پس باید مساحت جانبی یک استوانه و مساحت یک کره را با هم جمع کنیم. اگر مساحت جانبی استوانه را با \(\Large S_c\) و مساحت کره را با \(\Large S_s\) نشان دهیم، داریم:
\(\LARGE S_c=2 \pi R h\)
\(\LARGE \Rightarrow S_c=2 \times 3 \times 2 \times 5\)
\(\LARGE \Rightarrow S_c=60\)
\(\LARGE S_s=4 \pi R^2\)
\(\LARGE \Rightarrow S_s=4 \times 3 \times 2^2\)
\(\LARGE \Rightarrow S_s=48\)
بنابراین مساحت کل که از مجموع مساحت جانبی استوانه و مساحت کره به دست میآید، برابر است با:
\(\LARGE S=S_c+S_s=60+48\)
\(\LARGE \Rightarrow S=108\)
زنگ آخر کلاس حجم و مساحت کره ریاضی نهم
در درسنامهای که از ریاضی نهم خواندیم، ابتدا تعریف دایره و کره را بیان کردیم. سپس، به بررسی محاسبهٔ حجم و سطح کره پرداختیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با حجم و مساحت کره ریاضی نهم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





سپاس
ممنون
عالی