روابط بین زاویه ها ریاضی هفتم ✳️☄️ – رابطشونو پیدا کن!

در درسنامۀ روابط بین زاویه ها ریاضی هفتم به پرسش‌های زیر پاسخ می‌دهیم:

• نام‌گذاری زوایا چگونه انجام می‌شود؟
• اندازۀ زوایا چه ارتباطی به هم دارند؟
• آیا می‌توان مثلث‌ها را بر اساس اندازۀ زوایایشان دسته‌بندی کرد؟
• چند ضلعی های محدب و مقعر چیستند؟
• چند ضلعی های منتظم کدامند؟

درسنامه را طوری تنظیم کردیم تا با مطالعۀ آن، هیچ مشکلی در درک مبحث روابط بین زاویه ها ریاضی هفتم نداشته باشید. با ما تا انتها همراه باشید.

نحوۀ نام‌‌گذاری زوایا در روابط بین زاویه ها ریاضی هفتم

یک زاویه را می‌توانیم به روش‌های گوناگون نمایش دهیم. به شکل زیر نگاه کنید:

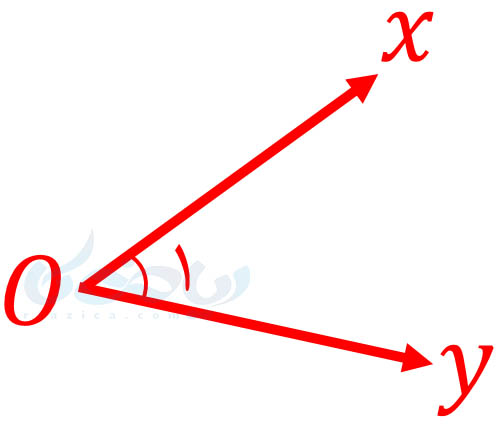
هم ‌می‌توانیم زاویۀ موجود در شکل بالا را تنها با رأس آن نشان دهیم. یعنی بنویسیم \(\Large \hat{O} \) یا \(\Large \hat{O_1} \) یا \(\Large \hat{1} \). هم می‌توانیم با سه حرف نشان دهیم. مثلاً بنویسیم \(\Large x\hat{O} y\) یا \(\Large y\hat{O} x\). در این صورت فقط باید حواسمان باشد که رأس را به عنوان حرف دوم بنویسیم. ترتیب دو حرف دیگر مهم نیست. دقت کنید در هر دو صورت، رأس را که یک نقطه است، با حرف بزرگ نشان می‌دهیم و دو حرف دیگر را که تعیین کنندۀ دو نیم‌خط هستند، با حرف کوچک نشان می‌دهیم (در صورتی که روش نام گذاری نیم‌خط و پاره‌خط را فراموش کرده‌اید، درسنامۀ روابط بین پاره خط ها را مرور کنید). در قسمت بعدی از درسنامۀ روابط بین زاویه ها ریاضی هفتم به بررسی روابط بین زوایا می‌پردازیم.

روابط بین زاویه‌ ها ریاضی هفتم

می‌توانیم زوایا را با یکدیگر مقایسه کرده یا اندازۀ آن‌ها‌ را به دست آوریم. همچنین می‌توانیم با بررسی روابط بین زوایای مختلف به تساوی‌های مطلوبی دست یابیم. در مثال‌های بعدی از درسنامۀ روابط بین زاویه ها ریاضی هفتم به بررسی همین‌روابط و تساوی‌ها می‌پردازیم.

مثال از روابط بین زاویه‌ ها ریاضی هفتم

مثال 1: با توجه به شکل زیر، هر یک از عبارت‌های \(\Large a\hat{O} b-\hat{O_1}\) و \(\Large \hat{O_1}+x\hat{O} b\) برابر با چه زاویه‌ای هستند؟

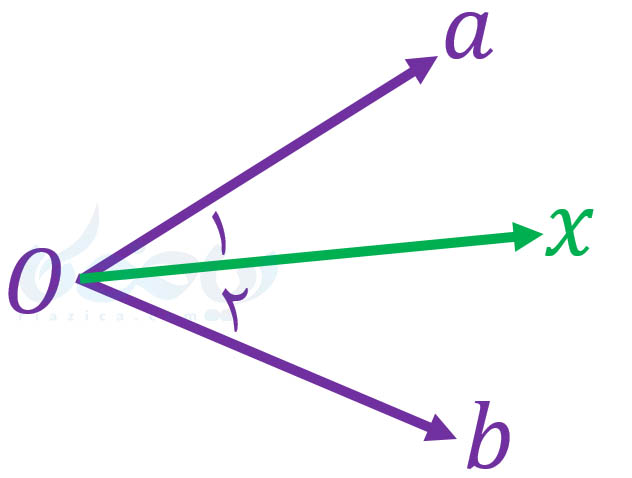
حل: همان‌طور که از شکل بالا مشخص است، از تفاضل زاویۀ \(\Large \hat{O_1}\) از \(\Large a\hat{O} b\)، زاویۀ \(\Large \hat{O_2}\) به دست می‌آید. از مجموع زاویۀ \(\Large \hat{O_1}\) و \(\Large x\hat{O} b\) نیز، زاویۀ \(\Large a\hat{O} b\) به دست می‌آید. بنابراین داریم:

\(\LARGE a\hat{O} b-\hat{O_1}=\hat{O_2}\)

\(\LARGE \hat{O_1}+x\hat{O} b=a\hat{O} b\)

به مثال‌ بعدی از درسنامۀ روابط بین زاویه ها ریاضی هفتم توجه کنید.

برابری زوایای متقابل به رأس

مثال 2: به شکل زیر نگاه کنید. دو زاویۀ \(\Large \hat{A_1}\) و \(\Large \hat{A_3}\) را اصطلاحاً متقابل به رأس می‌گوییم. دو زاویۀ \(\Large \hat{A_2}\) و \(\Large \hat{A_4}\) نیز متقابل به رأس هستند. ثابت کنید \(\Large \hat{A_1}=\hat{A_3}\) و \(\Large \hat{A_2}=\hat{A_4}\).

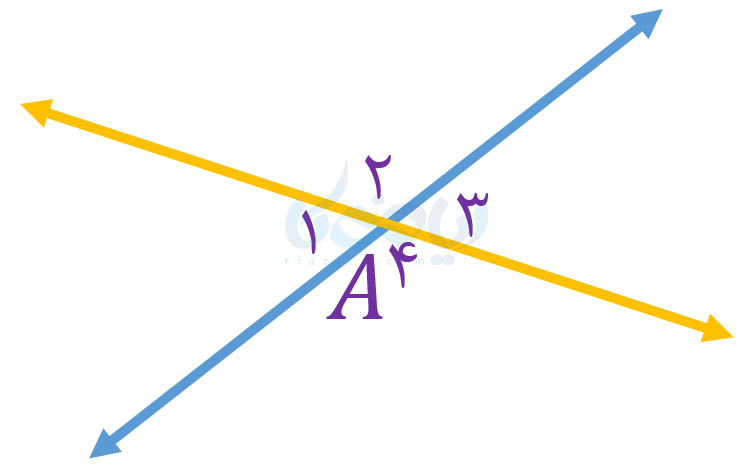
حل: از برابری زوایای متقابل به رأس در حل بسیاری از مسائل استفاده می‌شود. بنابراین به این مثال بسیار دقت کنید! ابتدا ثابت می‌کنیم \(\Large \hat{A_1}=\hat{A_3}\):

حال \(\Large \hat{A_2}=\hat{A_4}\) را اثبات می‌کنیم:

از برابری زوایای متقابل به رأس در حل مثال‌های قست بعد نیز کمک خواهیم گرفت. به قسمت بعدی از درسنامۀ روابط بین زاویه ها ریاضی هفتم توجه کنید.

پیداکردن اندازۀ زوایای مجهول

مثال 3: در شکل زیر، اندازۀ زوایه‌های \(\Large x\) و \(\Large y\) و \(\Large z\) را بیابید.

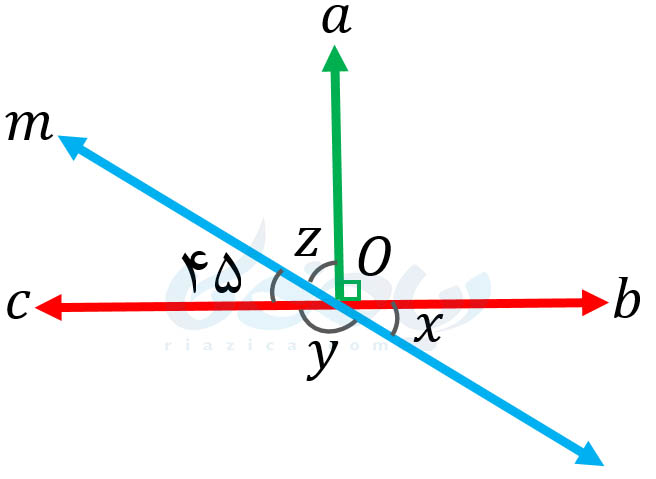
حل: از آتجاییکه زوایای \(\Large a\hat{O} b\) و \(\Large a\hat{O} c\) مکمل یکدیگرند (یعنی مجموعشان \(\Large 180\) درجه است)، داریم:

\(\LARGE 90+(\hat{z} +45)=180\)

\(\LARGE \Rightarrow \hat{z} +45=90\)

\(\LARGE \Rightarrow \hat{z}=45\)

همچنین از آنجاییکه زوایای \(\Large m\hat{O} c\) و \(\Large \hat{x} \) متقابل به رأس هستند، با یکدیگر برابرند. بنابراین \(\Large \hat{x}=45 \). زوایای \(\Large \hat{x} \) و \(\Large \hat{y} \) نیز مکمل‌اند. بنابراین داریم:

\(\LARGE \hat{x}+\hat{y}=180\)

\(\LARGE \Rightarrow 45+\hat{y}=180\)

\(\LARGE \Rightarrow \hat{y}=135\)

به مثال بعدی از درسنامۀ روابط بین زاویه ها ریاضی هفتم توجه کنید.

پیدا کردن زاویه در مثلث قائم‌الزاویه

مثال 4: در شکل زیر، اندازۀ زوایۀ \(\Large x\) را بیابید.

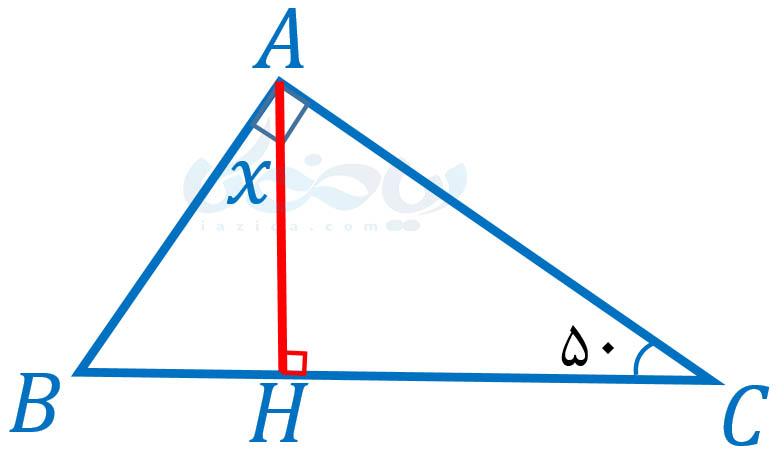
حل: مجموع زوایای مثلث \(\Large ABC \) برابر با \(\Large 180 \) درجه است. بنابراین داریم: 

\(\LARGE 90+50+\hat{B}=180 \)

\(\LARGE \Rightarrow \hat{B}=40 \)

از طرفی مجموع زوایای مثلث \(\Large ABH \) نیز برابر با \(\Large 180 \) درجه است. بنابراین داریم:

\(\LARGE 90+40+\hat{x}=180 \)

\(\LARGE \Rightarrow \hat{x}=50 \)

به قسمت بعدی از درسنامۀ روابط بین زاویه ها ریاضی هفتم توجه کنید.

انواع مثلث‌ها

می‌توانیم مثلث‌ها را با توجه به زوایه‌هایشان به سه دستۀ زیر تقسیم کنیم:

• مثلث‌های دارای سه زاویۀ تند
• مثلث‌های دارای یک زاویۀ راست
• مثلث‌های دارای یک زاویۀ باز

هیچ مثلثی نمی‌تواند دو زاویۀ راست داشته باشد. زیرا در این صورت، مجموع آن دو زاویه برابر با \(\Large 180\) درجه شده و زاویۀ سوم به ناچار باید صفر باشد که این غیر ممکن است. بنابراین اگر مثلث، یک زاویۀ راست داشته باشد، هر یک از زوایای دیگر باید تند باشند تا مجموع زوایا بیشتر از \(\Large 180\) درجه نشود. 

اگر مثلثی یک زاویۀ باز داشته باشد، هیچ کدام از دو زوایۀ دیگر، نه می‌توانند باز باشند، نه می‌توانند راست باشند. زیرا در این صورت مجموع زوایای مثلث بیشتر از \(\Large 180\) درجه خواهد شد. در نتیجه، هر دو زاویۀ باقی مانده تند خواهند بود. به مثال بعدی از درسنامۀ روابط بین زاویه ها ریاضی هفتم دقت کنید.

یاد آوری: به زاویه کمتر از ۹۰درجه زاویه تند (حاده)و به زاویه ۹۰ درجه زاویه راست(قائمه)وبه زاویه بیشتر از ۹۰ درجه زاویه باز (منفرجه) می‌گویند.

مثال از دسته‌بندی مثلث‌ها

مثال 5: مثلث متساوی‌الاضلاع در کدام یک از دسته‌هایی که معرفی کردیم، قرار می‌گیرد؟ مثلث متساوی‌الساقین چه طور؟

حل: همۀ زوایای مثلث متساوی الاضلاع برابر با \(\Large 60\) درجه است. بنابراین همۀ زوایای مثلث متساوی الاضلاع، تند هستند و در دستۀ اول قرار می‌گیرد. اما برای مثلث متساوی الساقین، زوایا مشخص نیستند. در هر سه دسته می‌توانم مثلث متساوی الساقین داشته باشیم. بیایید هر دسته را بررسی کنیم:

• دستۀ اول: هر مثلث متساوی الاضلاع، یک مثلث متساوی الساقین نیز هست. بنابراین مثلث متساوی‌الساقین با سه زوایۀ تند وجود دارد. البته مثلث‌های متساوی‌الساقین دیگری نیز وجود دارند که دارای سه زاویۀ تند هستند. مثلاً مثلثی با یک زاویۀ \(\Large 80\) درجه و دو زاویۀ \(\Large 50\) درجه.
• دستۀ دوم: مثلثی با یک زاویۀ \(\Large 90\) درجه و دو زاویۀ \(\Large 45\) درجه، هم متساوی‌الساقین است و هم زوایۀ راست دارد.
• دستۀ سوم: مثلثی با یک زاویۀ \(\Large 160\) درجه و دو زاویۀ \(\Large 10\) درجه، هم متساوی‌الساقین است و هم زوایۀ باز دارد.

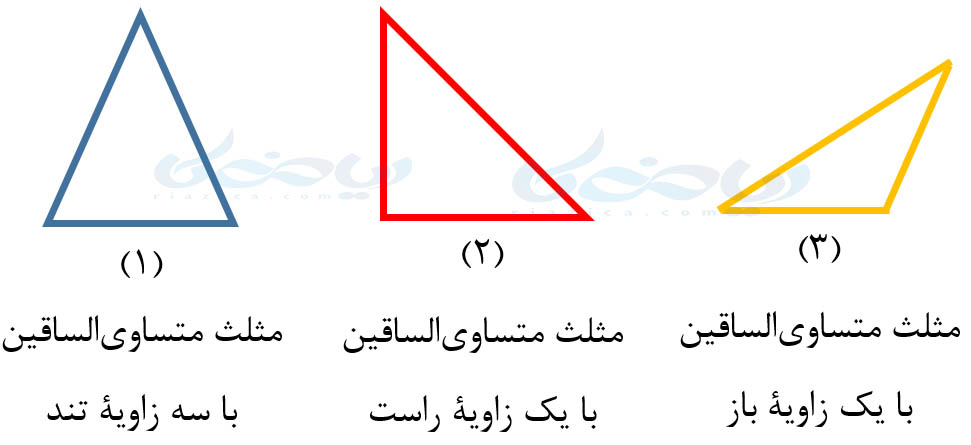
برای اینکه بهتر متوجه شوید، در شکل زیر از درسنامۀ روابط بین زاویه ها ریاضی هفتم از هر دسته، یک مثلث متساوی‌الساقین رسم کرده‌ایم:

چند ضلعی های محدب و مقعر

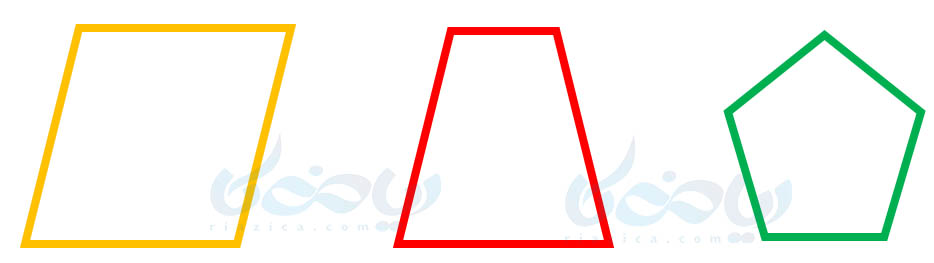
به چندضلعی‌هایی که زاویۀ بزرگتر از \(\Large 180\) درجه نداشته باشند، چندضلعی محدب (کوژ) می‌گوییم. چندضلعی‌های شکل زیر، همگی محدب هستند؛ زیرا هیچ کدام زاویه‌ای بزرگتر از \(\Large 180\) درجه ندارند:

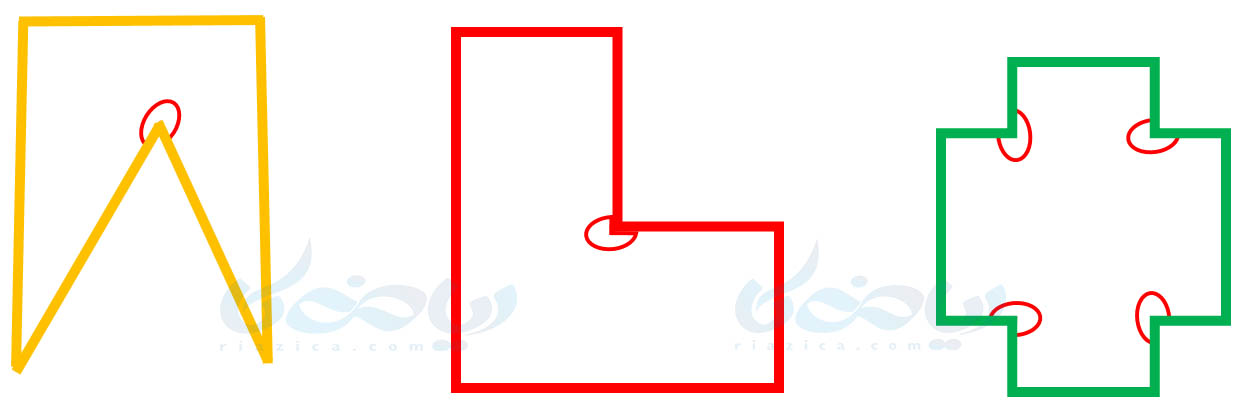
به چندضلعی‌هایی که حداقل یک زاویۀ بزرگتر از \(\Large 180\) درجه داشته باشند، چندضلعی مقعر (کاو) می‌گوییم. چندضلعی‌های شکل زیر، همگی مقعر هستند؛ زیرا هر کدام حداقل یک زاویۀ بیشتر از \(\Large 180\) درجه دارند که با رنگ قرمز مشخص شده‌ است:

برای مطالعۀ بیشتر: در صورتی که علاقه‌مندید می‌توانید در مورد مجموعه‌های محدب مطالعه کنید.

چندضلعی منتظم

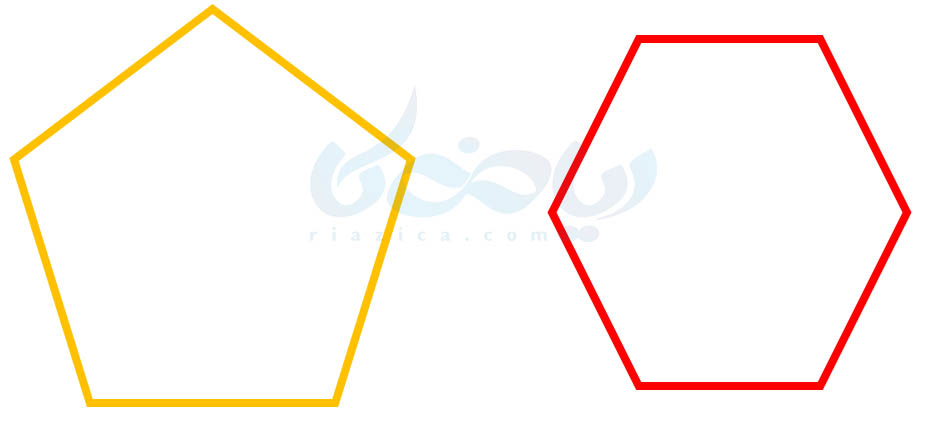
به چند ضلعی‌هایی که دارای ضلع‌ها و زوایای هم‌اندازه هستند، چند ضلعی منتظم می‌گوییم. مثلث متساوی‌الاضلاع سه‌ضلعی متنظم است. زیرا ضلع‌هایش با هم برابرند و تمام زوایایش \(\Large 60\) درجه هستند. مربع نیز چهارضلعی منتظم است. زیرا تمام ضلع‌هایش با یکدیگر برابرند و تمام زوایایش \(\Large 90\) درجه هستند. در شکل زیر از درسنامۀ روابط بین زاویه ها ریاضی هفتم پنج ضلعی و شش ضلعی منتظم را مشاهده می‌کنید.

برای خوندن ادامه مطلب به پست تبدیلات هندسی ریاضی هفتم مراجعه کنید.

زنگ آخر کلاس روابط بین زاویه ها ریاضی هفتم

در این درسنامه از ریاضی هفتم ابتدا روش نام گذاری زوایا را بررسی کردیم. سپس با حل مثال‌های مختلف، به بررسی روابط بین زوایای مختلف پرداختیم. در ادامه، مثلث‌ها را بر اساس زوایایی که داشتند به سه دسته تقسیم کردیم. در پایان هم، چند ضلعی های محدب و مقعر و همچنین چند ضلعی منتظم را معرفی کردیم.

ما در ریاضیکا آماده‌ی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث روابط بین زاویه ها ریاضی هفتم دارید، در دیدگاه‌ها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند ‌داد.