آموزش ریاضی پایه یازدهم تجربی
حل معادله رادیکالی 📝✅ – گام به گام با مثال و توضیحات!
گاهی در حل مسائل ریاضی و فیزیک و غیره به حل معادله رادیکالی برمیخوریم. بنابراین لازم است حل معادلات رادیکالی را فرا بگیریم. ما در این پست در مورد دامنه رادیکالی و حل معادلات رادیکالی برای شما مطالب و مثالهایی را بیان خواهم کرد.
تعریف معادله رادیکالی
معادلاتی که در آن عبارت رادیکالی شامل مجهول وجود داشته باشد یک معادله رادیکالی نامیده میشود در زیر مثالهایی از معادلات رادیکالی آورده شده است.
\(\LARGE \sqrt {x+7} = 5 \)
\(\LARGE x – \sqrt {2x-1} = 3 \)
\(\LARGE \sqrt {3x-1} + 5 = \sqrt {x+2} \)
\(\LARGE \sqrt {(x-1)^2 + 9} = 5 \)
دامنه معادلات رادیکالی
میدانیم در یک عبارت رادیکالی با فرجه زوج زیر رادیکال باید همیشه بزرگتر یا مساوی صفر باشد چون اعداد منفی ریشه زوج ندارند. پس در یک عبارت رادیکالی یا معادله رادیکالی باید دقت داشته باشید مقادیری به جای \(\Large x \) میتواند قرار بگیرد که عبارت زیر رادیکال را مثبت یا صفر کند یعمی دامنه یک تابع رادیکالی ساده مانند \(\Large y=\sqrt{x} \) برابر است با:
\(\LARGE D=[0,+\infty) \)
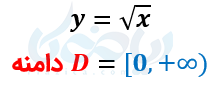
مثال ۱: دامنه معادلات زیر را پیدا کنید.
الف)
\(\LARGE 2\sqrt{x} = \sqrt{3x-3} \)
ب)
\(\LARGE 2\sqrt{2x-1} – x = 1 \)
ج)
\(\LARGE \sqrt{2x+4} +\sqrt{1-x} \)
\(\LARGE = \sqrt{2} \times (x-3) \)
الف)
برای پیدا کردن دامنه این معادله باید هر دو عبارت زیر رادیکال را بزرگتر مساوی صفر قرار دهیم و سپس بین دو جواب نامعادلات به وجود آمده را اشتراک بگیریم.
\(\LARGE x \geq 0 \rightarrow (1) \)
\(\LARGE 3x-3 \geq 0 \rightarrow x \geq 1 \rightarrow (2) \)
\(\LARGE (1) \cap (2) \rightarrow x \geq 1 \)
\(\LARGE D_f=[1,+\infty) \)
ب)
ابتدا رادیکال تنها میکنیم.
\(\LARGE 2\sqrt{2x-1} = 1+x \)
\(\LARGE 2x-1 \geq 0 \rightarrow x \geq \frac{1}{2} \rightarrow (1) \)
\(\LARGE 1+x \geq 0 \rightarrow x \geq -1 \rightarrow (2) \)
چون طرف اول نامنفی است باید طرف دوم نیز نامنفی باشد.
\(\LARGE (1) \cap (2) \rightarrow x \geq \frac{1}{2} \)
\(\LARGE D_f=[\frac{1}{2},+\infty) \)
ج)
\(\LARGE 2x+4 \geq 0 \rightarrow x \geq -2 \)
\(\LARGE 1-x \geq 0 \rightarrow x \leq 1 \)
\(\LARGE x+3 \geq 0 \rightarrow x \geq 3 \)
چون طرف اول نامنفی است.
اشتراک میگیریم همگی را:
\(\LARGE D_f=[-2,1] \)
حل معادله رادیکالی (معادلات گنگ)
برای حل معادله رادیکالی هدف این است که با استفاده از به توانهای مناسب رساندن طرفین و در صورت لزوم نکرار این روند رادیکالها را از بین ببریم و معادله را به معادلات چندجملهای ساده تبدیل کنیم و آنها را با توجه به درجهشان حل کنیم. برای سادگی محاسبات و کوتاهتر شدن آن، بهتر است با جابجایی عبارتها، رادیکالها را تنها کرده و سپس به توان برسانیم.
پس جوابهای بدست آمده را در معادله اولیه گذاشته و جوابهای قابل قبول را پیدا میکنیم یا با توجه به دامنه جوابهای قابل قبول را جدا کنیم.
مثال ۲: معادله زیر را حل کنید.
\(\LARGE \sqrt{x+6} = x \)
جواب ۲:
طرفین را به توان ۲ میرسانیم:
\(\LARGE x+6= x^2 \)
\(\LARGE x^2-x-6= 0 \)
\(\LARGE (x-3)(x+2)= 0 \)
\(\LARGE x=3,x=-2 \)
حال میبینیم آیا جوابها بدست آمده قابل قبول است.
راه اول:
\(\LARGE x=3 \)
\(\LARGE \sqrt{3+6}= 3 \)
\(\LARGE 3=3 \)
قابل قبول است.
\(\LARGE x=-2 \)
\(\LARGE \sqrt{-2+6}= -2 \)
\(\LARGE 2=-2 \)
غیر قابل قبول است.
راه دوم:
میتوانیم ابتدا دامنه این معادله را بدست آوریم و با توجه به آن جواب غیر قابل قبول را پیدا کنیم.
\(\LARGE x+6 \geq 0 \rightarrow x \geq -6 \)
\(\LARGE x \geq 0 \)
طرف اول نامنفی پس طرف دوم نیز نامنفی باید باشد.
\(\LARGE D_f=[0,+\infty) \)
پس جواب \(\Large x=-2 \) در دامنه این معادله نیست و قابل قبول نیست.
نکته: گاهی جوابها داخل دامنه نیز در معادله صدق نمیکنند و قابل قبول نیستند.
مثال ۳: معادله رادیکالی زیر را حل کنید.
\(\LARGE 2x= 1-\sqrt{2-x} \)
جواب ۳:
\(\LARGE \sqrt{2-x} = 1-2x \)
\(\LARGE 2-x = (1-2x)^2 \)
\(\LARGE 2-x = 1-4x+4x^2 \)
\(\LARGE 4x^2-3x-1=0 \)
\(\LARGE \Delta = 9 + 16 = 25 \)
\(\LARGE x=\frac{3 \pm 5}{8} \)
\(\LARGE x=1 , x=-\frac{1}{4} \)
حال ببینیم کدام جواب قابل قبول است.
راه اول:
\(\LARGE x=1 \)
\(\LARGE 2\times 1 = 1 – \sqrt{2-1} \)
\(\LARGE 2=0 \)
غیر قابل قبول است.
\(\LARGE x=-\frac{1}{4} \)
\(\LARGE 2\times -\frac{1}{4} = 1 – \sqrt{2-(-\frac{1}{4})} \)
\(\LARGE -\frac{1}{2}=-\frac{1}{2} \)
قابل قبول است.
راه دوم:
دامنه این معادله به صورت زیر محاسبه میشود:
\(\LARGE 2-x \geq 0 \rightarrow x \leq 2 \rightarrow (1) \)
\(\LARGE 1-2x \geq 0 \rightarrow x \leq \frac{1}{2} \rightarrow (2) \)
\(\LARGE (1) \cap (2) \rightarrow D_f=(-\infty,\frac{1}{2}] \)
با توجه به دامنه \(\Large x=1 \) غیر قابل قبول است.
مثال ۴: معادله رادیکالی زیر را حل کنید.
\(\LARGE \sqrt{x+7} = \sqrt{x} + 1 \)
جواب ۴:
به توان ۲ میرسانیم.
\(\LARGE x+7 = x+1 + 2\sqrt{x} \)
رادیکال را تنها میکنیم.
\(\LARGE 2\sqrt{x} = 6 \)
\(\LARGE \sqrt{x} = 3 \)
به توان ۲ میرسانیم.
\(\LARGE x=9 \)
قابل قبول است.
هم با توجه به دامنه و هم با توجه به اینکه \(\Large x=9 \) در معادله صدق میکند.
مثال۵:معادله زیر را حل کنید.
\(\LARGE \sqrt[3] {x+1} = 2 \)
طرفین به توان ۳ میرسانیم.
\(\LARGE x+1 = 8 \)
\(\LARGE x+7 \)
در مورد این مثال فرجه فرد است پس دامنه \(\Large \mathbb{R} \) میباشد. پس هر جواب که صدق کند قابل قبول است.
نکته در حل معادله رادیکالی: گاهی بعضی از معادلات را بدون حل کردن میتوان تشخیص داد که فاقد جواب هستند. به مثالهای زیر دقت کنید.
\(\LARGE \sqrt{x} + 5 = 0 \)
\(\LARGE \sqrt{1-x} + \sqrt{x+7} = 0 \)
\(\LARGE \sqrt{x-2} + \sqrt{2x+3} + 1 = 0 \)
در این معادلات چون مقادیر مثبت با هم جمع میشوند پس به ازای هیچ مقداری صفر نمیشوند پس معادلات جواب ندارد.
مثال تصویری از حل معادله رادیکالی

یک مثال کاربردی از حل معادله رادیکالی
فرض کنید دایرهای به مرکز \(\Large O(2,3) \) و شعاع ۵ سانتیمتر میخواهیم رسم کنیم.
تعیین کنید این دایره محور \(\Large x \)ها را در چه نقطه یا نقاطی قطع میکند.
فرض کنید دایره در یک نقطهی \(\Large A(x,0) \) محور \(\Large x \)ها را قطع کند فاصله \(\Large OA \) یا همان شعاع از رابطه زیر بدست میآید.
\(\LARGE OA \)
\(\LARGE = \sqrt{(x_A-x_O)^2+(y_A-y_O)^2} \)
\(\LARGE OA=5 \)
\(\LARGE 5= \sqrt{(x-2)^2+(0-3)^2} \)
\(\LARGE 25= (x-2)^2 + 9 \)
\(\LARGE (x-2)^2 =16 \)
\(\LARGE x-2=4 \rightarrow x=6 \)
\(\LARGE x-2=-4 \rightarrow x=-2 \)
که هر دو جواب هم قابل قبول هستند چون دامنه این معادله رادیکالی \(\Large \mathbb{R} \) میباشد. پس این دایره
محور \(\Large x \)ها را در دو نقطه قطع میکند.
\(\LARGE A(6,0) \)
\(\LARGE B(-2,0) \)
قبل از خواندن این پست درسنامه حل معادلات گویا را مطالعه کنید.
زنگ آخر حل معادله رادیکالی
خوب باهم عزیزان بحث حل معادله رادیکالی از ریاضی یازدهم تجربی را آوردیم. این مبحث آسان و به شدت کاربردی است. همیشه حواستان به دامنه معادلات رادیکالی باشد.
هر سوالی از حل معادله رادیکالی داشتید میتوانید در قسمت دیدگاه بنویسید کارشناسان ریاضیکا حتما به سوالاتتان پاسخ میدهند.





سلام.
رادیکالX2+4X+3 = X2+4x+5
این معادله رادیکالی چطور حل میشه؟
متشکر
با سلام وعرض ادب
سوال واضح نیست ایا طرف دوم هم رادیکال دارد؟
خیر تنها روی ایکس دو به علاوه چهار ایکس به علاوه پنج
سلام عرض ادب
از روش تغییر متغیر استفاده می کنیم به طوریکه x^2+4x+3 را t می گیریم و رادیکال x^2+4x+5 را رادیکال t+2 سپس طرفین را به توان دو رسانده و جواب های t را بدست می آوریم که جواب ها ۲ و ۱- می شود حالا آن ها برابر قرار داده و x را بدست می آوریم. (با شرط t>0)
موفق باشید.
خیر تنها طرف ایکس دو به علاوه چهار ایکس به علاوه پنج
سلام عرض ادب
از روش تغییر متغیر استفاده می کنیم به طوریکه x^2+4x+3 را t می گیریم و رادیکال x^2+4x+5 را رادیکال t+2 سپس طرفین را به توان دو رسانده و جواب های t را بدست می آوریم که جواب ها ۲ و ۱- می شود حالا آن ها برابر قرار داده و x را بدست می آوریم. (با شرط t>0)
موفق باشید.
ببخشید برای y=√5-x ممکنه یک مسئله کاربردی طرح کنید؟
سلام ممنون از مطالب شما
من درست متوجه مثال ج دامنه ها نشدم چطوری طرف راست تساوی محاسبه شده؟
با سلام
در مثال ج چون طرف اول تساوی یک عبارت همیشه مثبت می باشد باید طرف دوم نیز یک عبارت همیشه مثبت باشد برای همین آن را نیز بزرگتر از صفر میگذاریم
سلام معادله رادیکال ۶ +رادیکال x+3=رادیکال 2x_3
سلام چه موقع نمی شود با دامنه سوال را حل کرد
سلام دوست عزیز دامنه فقط تعیین میکنه جوابهای بدست آمده قابل قبول هستن یا نه روش حل نیست
فقط باید دقت کنید گاهی حتی جوابهایی که در دامنه هستن در معادله صدق نمیکنن پس حتما جوابهای داخل دامنه را در معادله قرار دهید
چه موقع روش دامنه جواب نمی دهد
در چه صورت دامنه معادله رادیکالی R میشه???
و چجوری تشخیص بدیم که معادله رادیکالی جواب داره یا نه???
سلام همین مقاله رو خوب بخونید به جواب میرسید