آموزش ریاضی پایه هفتم
راهبردهای حل مسئله ریاضی هفتم 🎣🤼♀️ – دیدتو به حل مسئله عوض کن!
در این درسنامه، راهبردهای حل مسئله ریاضی هفتم را بررسی میکنیم. قبل از این هم برای حل مسائل ریاضی از راهبردهای متفاوتی استفاده کردهاید. ممکن است اسامی یا توضیح بعضی از راهبردها در کتاب درسی برایتان نامفهوم باشد. برای هر راهبرد، مثالی حل میکنیم تا به خوبی آن را فرا بگیرید. پس با ما همراه باشید. هر سوالی هم که داشتید، در دیدگاهها بنویسید. به سرعت به سوالتان پاسخ میدهیم.
راهبرد رسم شکل در راهبردهای حل مسئله ریاضی هفتم
در بسیاری از مسائل، نیازی به رسم شکل نیست. با این حال، کشیدن یک شکل میتواند به شهود ما و درک بهتر مسئله کمک کند. گاهی حتی تجسم یک تصویر در ذهن بدون کشیدن آن، ما را به سمت روش حل مسئله هدایت میکند. به مثال زیر دقت کنید.
مثال از راهبرد رسم شکل
مثال 1: وسط اضلاع مربعی به ضلع 2 سانتیمتر را طوری به هم وصل میکنیم که یک مربع جدید تشکیل شود. مساحت مربع جدید چهقدر است؟
حل: برای داشتن درک بهتر از مسئله، شکل را رسم میکنیم. دقت کنید، نیازی به رسم شکل دقیق نیست. کافی است مطابق شکل زیر، مربع \(\Large ABCD\) را رسم کرده و وسط اضلاع مجاور را به هم وصل کنیم:
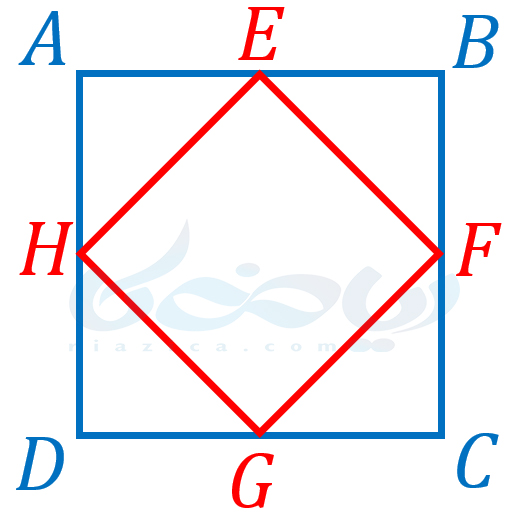
مربع جدید، مربع \(\Large EFGH\) است. همانطور که میبینید، قطرهای مربع جدید، برابر با اضلاع مربع اوّلیه است. یعنی داریم:
\(\LARGE EG=BC\)
\(\LARGE FH=AB\)
از آنجاییکه هر مربعی، لوزی هم هست، برای محاسبۀ مساحت میتوانیم اندازۀ دو قطر را در هم ضرب کرده و بر 2 نقسیم کنیم. چون قطرهای مربع جدید، برابر با اضلاع مربع اوّلیهاند، مساحت مربع جدید برابر است با:
\(\LARGE S=\frac{2\times 2}{2}=2\)
راهبرد الگوسازی در راهبردهای حل مسئله ریاضی هفتم
برای حل بعضی از مسائل لازم است تا حالات ممکن برای رخداد یک پدیده را پیدا کرده و یا شمارش کنیم. در حل این مسائل برای اینکه مطمئن باشیم تمامی حالات را بررسی کردهایم و چیزی از قلم نیفتاده، باید با نظم خاصی جلو برویم. مثلاً فرض کنید میخواهیم تمام اعداد 3 رقمی ممکن با ارقام 5 و 7 را پیدا کنیم. اگر به صورت تصادفی هر عددی که به ذهنمان میرسد را بنویسیم، در نهایت متوجه نخواهیم شد که آیا عددی جا افتاده یا همۀ اعداد را پیدا کردهایم. اگر جا افتاده چه عددی جا افتاده؟ در مثال زیر از درس راهبردهای حل مسئله ریاضی هفتم همین مسئله را با استفاده از راهبرد الگوسازی حل میکنیم (بهتر بود به جای عبارت راهبرد الگوسازی که کتاب درسی هفتم به کار برده، از عبارت “راهبرد بررسی حالات ممکن” استفاده میشد).
مثال از راهبرد الگوسازی
مثال 2: تمام اعداد 3 رقمی ممکن با ارقام 5 و 7 را بیابید.
حل: برای پیدا کردن حالات مختلف باید از یک نظم مشخص پیروی کنیم. ابتدا رقم دهگان و صدگان را ثابت فرض میکنیم و حالات ممکن را مینویسیم. بعد از اینکه حالات ممکن را برای آن دهگان و صدگان خاص نوشتیم، دهگان و صدگان را تغییر داده و جلو میرویم. هر جا که تمام حالات مختلف دهگان و صدگان بررسی شد، توقف کرده و با اطمینان میگوییم تمام حالات ممکن را بررسی کردهایم. اگر دهگان و صدگان هر دو 5 باشند، آنگاه یکان یکی از ارقام 5 یا 7 خواهد بود. بنابراین اعداد سه رقمی زیر به دست میآیند:

حال دهگان و صدگان را تغییر داده و به جای هر دو، 7 میگذاریم. در این صورت باز هم یکان، یکی از ارقام 5 یا 7 بوده و اعداد سه رقمی زیر به دست میآیند:

این بار دهگان را 5 و صدگان را 7 قرار میدهیم. مثل قبل، یکان، یکی از ارقام 5 یا 7 خواهد بود. بنابراین دو عدد زیر به دست میآیند:

فقط یک حالت دیگر برای دهگان و صدگان مانده. آن هم حالتی است که دهگان 7 و صدگان 5 باشد. در این صورت با در نظر گرفتن یکانهای 5 یا 7، اعداد زیر حاصل میشوند:

تمام حالات مختلف برای دهگان و صدگان و به دنبال آن برای یکان را بررسی کردهایم. حال با اطمینان میتوانیم بگوییم هیچ عددی جا نیفتاده است. به این روش منظم پیدا کردن حالات مختلف برای یک مسئله، به اصطلاح کتاب ریاضی هفتم، راهبرد الگوسازی میگوییم.
راهبرد حذف حالت های نامطلوب در راهبردهای حل مسئله ریاضی هفتم
برای حل بعضی از مسائل، ابتدا باید تعدادی حالت را پیدا کرده و سپس از بین آنها، حالتهای نامطلوب را کنار بگذاریم تا به جواب برسیم. به مثال زیر از درس راهبردهای حل مسئله ریاضی هفتم توجه کنید.
مثال از راهبرد حذف حالت های نامطلوب
مثال 3: حاصل ضرب سن سه نفر 30 و مجموع سنشان 14 است. کوچکترین نفر چند سال سن دارد؟
حل: با استفاده از راهبرد الگوسازی که در قسمت قبل توضیح دادیم، تمام حالتهایی را که ضرب سه عدد طبیعی برابر با 30 میشود، پیدا میکنیم. سپس، از بین حالتهای به دست آمده، حالتی را انتخاب میکنیم که مجموع سه عدد برابر 14 باشد و بقیۀ حالتها حذف میکنیم. برای پیدا کردن حالتهایی که ضرب سه عدد طبیعی 30 شود، ابتدا حالتی را در نظر میگیریم که دو عدد از سه عدد برابر با 1 باشد. در این صورت فقط سه عدد زیر را خواهیم داشت (دقت کنید که ترتیب اعداد برایمان مهم نیست):

حال به سراغ حالتی میرویم که فقط یکی از اعداد برابر با 1 باشد. در این صورت حاصل ضرب دو عدد دیگر باید برابر با 30 شود. کافی است هر بار، یک مقسومٌ علیه 30 (به غیر از 1 و30 که بررسی کردیم) را به عنوان عدد دوم در نظر گرفته و عدد سوم را از تقسیم 30 بر عدد دوم به دست آوریم. به این ترتیب، اعداد زیر به دست خواهند آمد:



در نهایت حالتی را بررسی میکنیم که هیچ یک از سه عدد، برابر با عدد 1 نباشد. در این صورت، تنها حاصل ضرب سه عدد زیر برابر با 30 میشود:

به این صورت تمامی حالاتی که حاصل ضرب سه عدد طبیعی برابر با 30 میشود را بررسی کردیم. اگر تمامی حالات را در یک جدول بنویسیم و حالات نامطلوب را که جمع سه عدد برابر با 14 نیست، خط بزنیم، جدول زیر به دست میآید:

بنابراین سن این سه نفر، 1 و 3 و 10 است. در نتیجه، کوچکترین نفر، 1 سال دارد.
راهبرد الگویابی در راهبردهای حل مسئله ریاضی هفتم
در سالهای گذشته، معمولاً در فصل اول هر کتاب با الگویابی سر و کار داشتهاید. منظور کتاب از راهبرد الگویابی نیز روشی است که برای حل این مسائل به کار میبریم. برای پیدا کردن نظم و الگو در یک پدیده، نمیتوان یک راه معین برای تمام مسئلهها ارائه کرد. تنها، حل مسئلۀ زیاد باعث ورزیده شدن ذهن شما و افزایش خلاقیتتان جهت پیدا کردن الگو میشود. برای اینکه مروری کرده باشیم بر مسائل الگویابی، به مثال زیر از درس راهبردهای حل مسئله ریاضی هفتم توجه کنید.
مثال از راهبرد الگویابی
مثال 4: با توجه به شکلهای زیر، در شکل دهم چند پارهخط خواهیم داشت؟
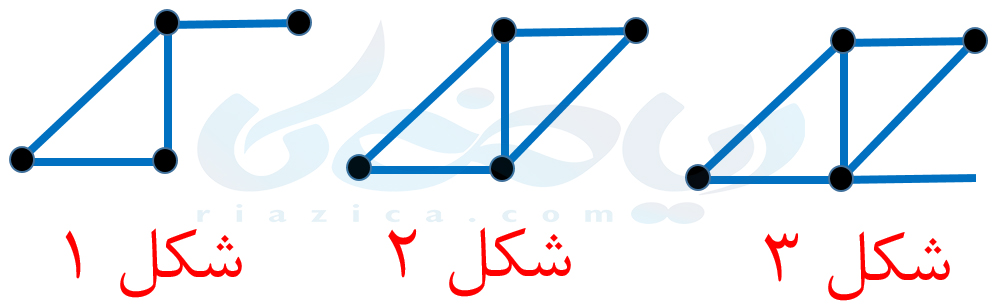
حل: اگر دقت کنید، در هر شکل یک مثلث داریم که به تعداد شمارۀ هر مرحله، به آن پاره خط اضافه شده. بنابراین در شکل دهم نیز، یک مثلث خواهیم داشت که به آن ده پاره خط نیز اضافه شده است. در نتیجه شکل دهم 13 پارهخط خواهد داشت.
راهبرد حدس و آزمایش در راهبردهای حل مسئله ریاضی هفتم
برای حل بعضی از مسائل نیاز به بررسی تعداد محدودی از حالتها داریم. در این صورت میتوانیم از آزمایش حالات محتلف استفاده کنیم. از ترکیب این راهبرد و دیگر راهبردها میتوان برای حل مسائل پیچیدهتر نیز استفاده کرد. به مثال زیر از درس راهبردهای حل مسئله ریاضی هفتم توجه کنید.
مثال از راهبرد حدس و آزمایش
مثال 5: تعدادی سکۀ 100 تومانی و تعدادی سکۀ 50 تومانی داریم. به چه روشی چند سکه انتخاب کنیم که مجموع مقادیر آنها 400 تومان شده و تعداد سکهها 6 تا باشد؟
حل: برای اینکه ببینیم، در چه حالتی 6 سکه خواهیم داشت، حالات مختلفی که مجموع ارزش سکهها 400 تومان میشود را در جدول زیر آزمایش میکنیم:
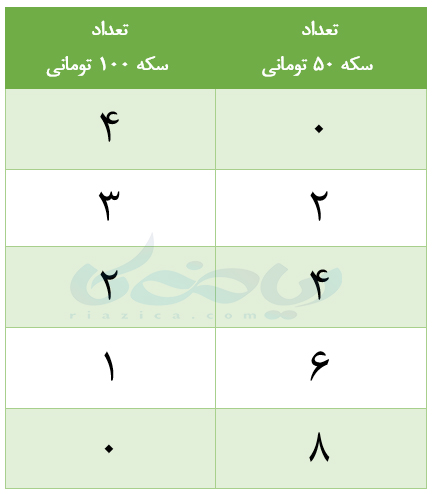
همانطور که از جدول بالا پیداست، در حالتی که از 2 سکۀ 100 تومانی و 4 سکۀ 50 تومانی استفاده کنیم، از 6 سکه استفاده کردهایم.
راهبرد زیرمسئله در راهبردهای حل مسئله ریاضی هفتم
بسیاری از مسائل را میتوان به قسمتهای کوچک تر و تعدادی زیرمسئله تقسیم کرد. بدون شک قبل از خواندن این درسنامه نیز از این راهبرد به کرات استفاده کردهاید. به مثال زیر از درس راهبردهای حل مسئله ریاضی هفتم توجه کنید.
مثال از راهبرد زیرمسئله
مثال 6: فروشندهای 4 تلفن هوشمند هر کدام به قیمت 200 یورو و 6 رایانه هر کدام به قیمت 600 یورو خریداری میکند. اگر او هر تلفن هوشمند را به قیمت 210 یورو و هر رایانه را به قیمت 630 یورو بفروشد، چه قدر سود کردهاست؟
حل: میتوانیم مسئله را به دو زیرمسئله تقسیم کنیم. ابتدا هزینهای که فروشنده برای تلفن هوشمند و رایانه کرده را محاسبه کنیم. سپس، مقدار درآمدی که از فروش آنها داشته را به دست آوریم. در نهایت از تفاضل مقادیر به دست آمده، سود فروشنده به دست میآید. هزینهای که فروشنده کرده برابر است با:
\(\LARGE 4\times 200+6\times 600=4400\)
از طرفی درآمد فروشنده برابر است با:
\(\LARGE 4\times 210+6\times 630=4620\)
بنابراین سود فروشنده برابر است با:
\(\LARGE 4620-4400=220\)
راهبرد حل مسئله ساده تر در راهبردهای حل مسئله ریاضی هفتم
زمانی که در یک مسئله با اعداد بزرگ، تعداد زیاد و یا حالتهای پیچیده سر و کار داریم، حل حالت خاصی از مسئله و یا صورت ساده شدۀ آن میتواند به ما در پیدا کردن راه حل مسئلۀ اصلی کمک کند. به مثال زیر از درس راهبردهای حل مسئله ریاضی هفتم توجه کنید.
مثال از راهبرد حل مسئلۀ سادهتر
مثال 7: حاصل عبارت زیر را به دست آورید.
\(\LARGE 1+3+5+\dots+99\)
حل: عبارت بالا، مجموع اعداد طبیعی فرد کوچکتر از 100 است. بگذارید مسئله را برای اعداد کوچکتر حل کنیم. مجموع اعداد طبیعی فرد کوچکتر مساوی 1، 3، 5 و 7 را به دست میآوریم:
\(\LARGE 1=1\)
\(\LARGE 1+3=4\)
\(\LARGE 1+3+5=9\)
\(\LARGE 1+3+5+7=16\)
اگر دقت کنید، در هر مرحله یک مربع کامل به دست آمد. اگر عدد آخری که جمع میشود \(\Large 2n-1\) باشد، حاصل مجموع \(\Large n^2\) است. مثلاً در مرحلۀ سوم، عدد آخری که جمع میشود، 5 است که میتوانیم آن را به صورت \(\Large 2\times 3-1\) بنویسیم. در نتیجه حاصل عبارت سوم نیز \(\Large 3^2\) شد. برگردیم به مسئلۀ اصلی! میخواستیم حاصل عبارت زیر را پیدا کنیم:
\(\LARGE 1+3+5+\dots+99\)
عدد آخری که در عبارت بالا جمع میشود، 99 است که میتوانیم آن را به صورت \(\Large 2\times 50-1\) بنویسیم. بنابراین باتوجه به مراحل ساده شدهای که طی کردیم، پاسخ مثال، برابر با \(\Large 50^2\) خواهد بود.
راهبرد روش های نمادین در راهبردهای حل مسئله ریاضی هفتم
گاهی اوقات با مسائلی روبهرو هستیم که مقدار یک کمیت را نمیدانیم، اما اگر به جای آن از یک نماد استفاده کرده و با آن مثل یک عدد معلوم برخورد کنیم، مسئله به سادگی حل میشود. برای اینکه بهتر متوجه شوید، به مثال زیر از درس راهبردهای حل مسئله ریاضی هفتم توجه کنید.
مثال از راهبرد روش های نمادین(نوشتن معادله)
مثال 8: عددی را 4 برابر کرده و 5 واحد از آن کم کردیم. حاصل 7 شد. عدد اولیه چند بوده است؟
حل: عدد اولیه را نمیدانیم. بنابراین به جای آن، از حرف \(\Large N\) استفاده میکنیم (از هر نماد دیگری نیز میتوانید استفاده کنید). با توجه به توضیح مسئله، تساوی زیر به دست میآید:
\(\LARGE 4\times N-5=7\)
در آینده در کتاب ریاضی نهم، به طور مفصل در مورد روش پیدا کردن مقدار \(\Large N\) در تساوی بالا صحبت خواهیم کرد. میتوانیم به دو طرف تساوی بالا، عدد 5 را اضافه کنیم تا به تساوی زیر برسیم:
\(\LARGE 4\times N-5+5=7+5\)
\(\LARGE \Rightarrow 4\times N=12\)
تساوی بالا به ما میگوید، حاصل ضرب یک عدد نا معلوم (که آن را با \(\Large N\) نمایش میدهیم) در 4 برابر با 12 است. چه عددی ضرب در 4 برابر با 12 خواهد شد؟ کاملاً درست است، عدد 3. بنابراین عدد اولیه که آن را با \(\Large N\) نمایش دادیم، همان عدد 3 است.
زنگ آخر کلاس راهبردهای حل مسئله ریاضی هفتم
راهبردهای حل مسئله در کتاب ریاضی هفتم را به همراه حل مثال از هرکدام بررسی کردیم. در حل مسائل مختلف ریاضی میتوان این راهبردها را اتخاذ کرد. در حل مثالها سعی کردیم منظور کتاب از هر راهبرد و ورش به کار بردن آن راهبرد را برایتان به سادگی بیان کنیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث راهبردهای حل مسئله ریاضی هفتم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





خیلی راحت و روان توضیح داده شده بود ممنونم??
سلام. ممنون از نظری که دادید.
خواب جواب رابنویسید
سلام. چه جوابی؟
جواب عبارت ١+٣+۵+٧+…۴٩٩٩=
چیه ؟و چطوری حل میشه
سلام دوست عزیز
چون ۴۹۹۹ دوهزار وپانصدمین عدد فرد میباشد و میدانیم مجموع n عدد فرد برابر n^2 است پس جواب ابن سوال 2^2500 است.
عالیییی
سلام و عرض ادب
ممنون از انرژی و پیام پرمهرتون.
موفق باشید
درود
عالی بود❤
با سلام وعرض ادب ممنون از حسن ظن شما
سلام دبیر ارشد ریاضیکا تدریستون عالی هست .
من یه سوال داشتم چرا توی راهبرد حدس وآزمایش درسوالاتی که تعداد بسته ی 50و100تومانی را داده ابتدا در ستون اول تعداد بسته ی بزرگتر 100تومانی را می گذاریم لطف میکنید توضیح بدین
با سلام وعرض ادب
دوست عزیز فرقی نداره در کدوم ستون کدوم سکه رو بذاریم فقط باید جمع سطری ستونها چهارصد تومن بشه حالا همه حالتها را بررسی میکنیم
سلام خیلی عالیه ممنونم
من چندتا سوال داشتم میخواستم بگید تو چه مسئله هوایی باید مثلاً از راهبرد الگو سازی یا رسم شکل یا حل مسئله ساده تر و…….استفاده کنیم؟
چرا درراهبرد حدس و آزمایش درستون اول تعداد بسته بزرگتر یعنی100تومانی را باید بنویسیم چرا کوچکتر را نمی نویسیم ؟
با سلام
فرقی نداره کدوم اول باشه
سلام خیلی خیلی عالیه ممنونم
فقط چرا در راهبرد حدس و آزمایش تعداد بسته ی بزرگتر را درستون اول می نویسیم چرا بسته ی کوچکتر را درستون اول نمی نویسیم
لطف میکنید توضیح بدین
سلام یک مقسوم علیه 30یعنی چه؟
با سلام و عرض ادب
مقسوم علیه همان شمارنده است وقتی میگوییم مقسوعلیه عدد ۳۰ یعنی عددهایی که سی بر آنها بخش پذیر ایت
سلام دبیر ارشد ریاضیکا ممنونم از تدریس خوبتون میشه لطف کنید این سوال رو توضیح بدین
مجموع عددهای طبیعی از 1تا100را حساب کنید
با سلام وعرض ادب
کافیه ۱بعلاوه۱۰۰ کنید ضربدر تعداد عددها که صد تا هست بکنید تقسم بر دو
با سلام البته آقای کارل گاوس(ریاضیدان) این مسئله رو به این شکل راحتتر حل کرد:
اون ۱۰۰ رو با ۱جمع کرد شد۱۰۱ بعد ۹۹رو با۲ جمع کرد شد۱۰۱ و ازاین الگو استفاده کرد و نتیجه گیری کرد که میتونه بجای جمع کردن تک تک اعداد ، نصف تعدادشون رو در حاصلجمع اولین عدد با آخرین عدد ضرب کرده حاصلجمع کل رو به سادگی بدست بیاره!!!واقعا این فقط از یه نابغه بر میاد
بله دقیقا دوست عزیز
ببخشید من این راهبرد ها را برای آخرین سوال صفحه ۱۲ ریاضی هفتم می خوام ولی قاطی است میشه خلاصه کنید ؟
سلام من متاسفانه در راهبرد روش های نمادین مشکل دارم
با سلام وادب
با حل زیاد مسئله در آن تبحر پیدا کنید
با سلام دوست عزیز
وقتی امسال حل معادله رو یاد یگیرید بهتر با این روش آشنا میشوید
سلام خسته نباشید ببخشید ایا ممکن است در یک مسئله هم راهبر زیر مسئله هم روش های نمادین به کار برده شود
با سلام دوست عزیز
بله در حل یک مسئله گاهی از تلفیق چند روش استفاده می کنیم
میشه بهتر بگید خیلی اخه سختن من امتحانمستنر هم دارم ۲هفته دیگه بعد خوب نبود فقط یه ذره خو🤏فقط یه ذره🤏🤏
با سلام دوست عزیز
راه حل یاد گرفتن این درس حل کردن زیاد مسئله هست شما هر چی مسئله بیشتر حل کنی کم کم دست میاد که چه راهبردی استفاده کنی
من توصیه می کنم در حل مسئله اول صورت سوال خوب بفهمی داده های مسئله رو از اون بیرون بکشی وخواسته سوال برات واضح بشه اون موقع راه حل خودش رو نشون میده
سلام ممنونم بابت توضیحاتتون فقط من امتحان ترم اول دارم میشه بگید که ما دقیقا چطور باید روی مسئله ها تمرکز کنیم🙂؟
با سلام دوست عزیز
امیدوارم امتحانات رو خوب وعالی پشت سر بذارید
اول خوب صورت سوال رو بخونید تا متوجه خواسته سوال بشید بعد به معلومات سوال دقت کنید وببینید چطور از این معلومات به مجهولات برسید فقط زیاد مسئله حل کنید تا متبجپحر بشید