آموزش ریاضی پایه نهم
شیب خط و عرض از مبدا ریاضی نهم 🎢⏸ – خط بهتر بشناس!
در درسنامهٔ شیب خط و عرض از مبدا ریاضی نهم ، به معرفی شیب خط و عرض از مبدا پرداخته و این دو کمیت را برای خطوط مختلف به دست میآوریم. همچنین، معادلهٔ خطوط را با دانستن شیب و عرض از مبدا و یا نمودار آنها مینویسیم. در انتها نیز، شکل کلی معادلهٔ خط در فضای دو بعدی را معرفی میکنیم. سعیمان این است که با حل مثالهای مختلف، در درک بهتر این مبحث به شما کمک کنیم. با توجه به محتوای این درسنامه، پیشنهاد میکنیم قبل از شروع، درسنامهٔ معادله خط ریاضی نهم را مرور کنید. به اولین قسمت از درسنامهٔ شیب خط و عرض از مبدا ریاضی نهم توجه کنید.
شیب خط چیست؟
تعریف شیب خط: معادلهٔ خط در فضای دوبعدی را میتوان به صورت \(\Large y=ax+b\) نوشت. در این حالت به \(\Large a\)، شیب خط میگوییم.
به عبارت دیگر، در معادله خطی که ضریب \(\Large y\) برابر با \(\Large 1\) باشد، شیب خط برابر با ضریب \(\Large x\) خواهد بود. مثلاً، شیب خطی به معادلهٔ \(\Large y=2x+3\) برابر با \(\Large 2\) و شیب خطی به معادلهٔ \(\Large y=-x+1\) برابر با \(\Large -1\) است.
ارتباط شیب با زاویهٔ خط با جهت مثبت محور طولها
در شکل زیر، سه خط رسم شده و معادلهٔ هر یک نوشته شده است:
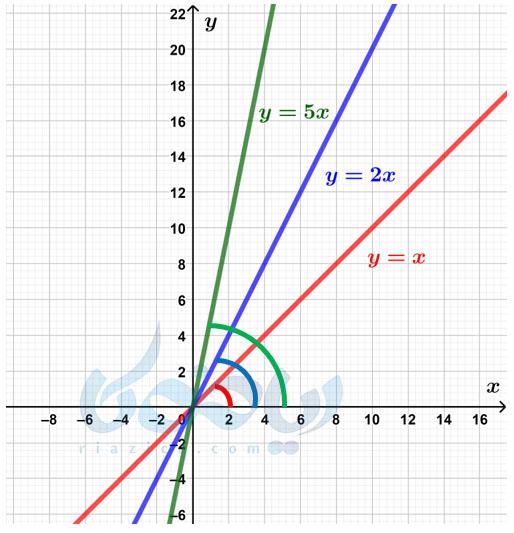
شیب خط قرمز رنگ برابر است با \(\Large 1\)، شیب خط آبی رنگ برابر است با \(\Large 2\) و شیب خط سبز رنگ برابر است با \(\Large 5\). همان طور که میبینید، هر چه قدر شیب خط بیشتر میشود، زاویهٔ خط نیز با جهت مثبت محور طولها افزایش مییابد. این با شهود ما نیز سازگار است. البته باید در نظر داشت که در شکل بالا شیب خطوط، مثبت بودند. برای خطوط با شیب منفی نیز میتوان جهت منفی محور طولها را در نظر گرفت و مقایسهٔ مشابهی بین خطوط با شیب منفی انجام داد.
چرا شیب خط را اینگونه تعریف میکنیم؟
همهٔ ما میتوانیم بدون اینکه چیزی از معادلهٔ خط بدانیم شیب دو سطح را با هم مقایسه کنیم. اگر بخواهیم بدون استفاده از روابط ریاضی و به صورت غیر دقیق شیب یک سطح را تعریف کنیم، میتوانیم بگوییم هر چه تغییرات عمودی بیشتری در یک جابجایی افقی اتفاق بیفتد، سطح مورد نظر ما دارای شیب بیشتری است. برای اینکه بهتر متوجه شوید، در دو حالت، سه سطح شیبدار را مقایسه میکنیم. در حالت اول، مقدار جابهجایی افقی را یکسان در نظر گرفته و مقدار جابهجایی عمودی را تغییر میدهیم. در حالت دوم، مقدار جابهجایی عمودی را یکسان در نظر گرفته و مقدار جابهجایی افقی را تغییر میدهیم.
حالت اول: جابهجایی افقی یکسان
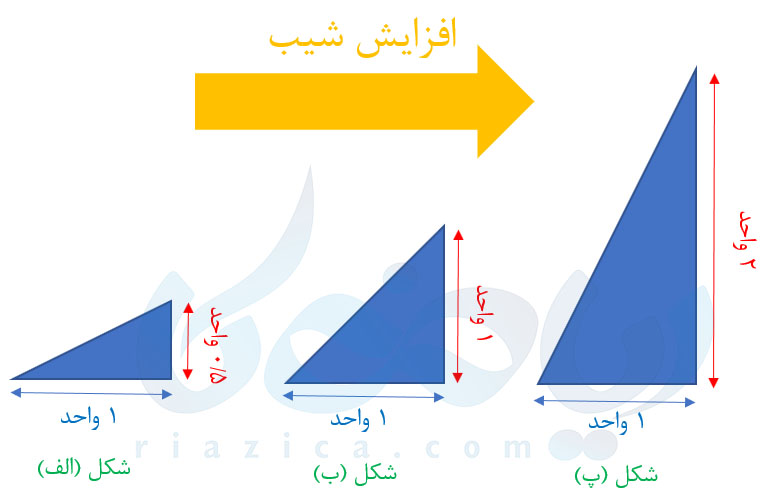
در هر کدام از سطوح بالا زمانی که به انتهای سطح شیبدار میرسیم، به اندازهٔ \(\Large 1\) واحد به صورت افقی جابهجا شدهایم؛ اما در سطح شیبدار “الف” به اندازهٔ \(\Large 0.5\) واحد، در سطح شیبدار “ب” به اندازهٔ \(\Large 1\) واحد و در سطح شیبدار “پ” به اندازهٔ \(\Large 2\) واحد به صورت عمودی جابهجا شدهایم. حسی هم که نسبت به شیب داریم به ما میگوید که شیب سطح شیبدارهای بالا از چپ به راست افزایش مییابد. بنابراین به ازای یک مقدار ثابت جابهجایی در راستای \(\Large x\)، هر چه قدر جابهجایی در راستای \(\Large y\) بیشتر باشد، شیب بیشتر است.
حالت دوم: جابهجایی عمودی یکسان
حال بیایید مقدار جابهجایی به صورت عمودی را ثابت در نظر گرفته و مقدار جابهجایی به صورت افقی را تغییر دهیم. به شکل زیر نگاه کنید:
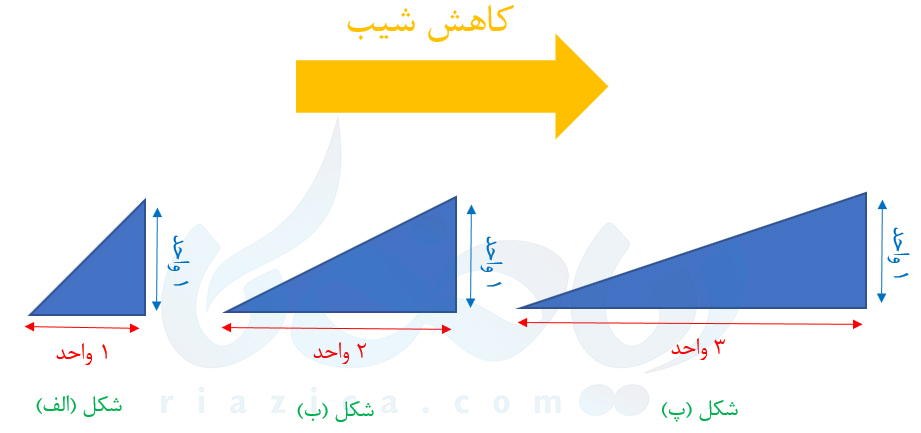
جابهجایی عمودی ما در هر سه سطح شیبدار به اندازهٔ \(\Large 1\) واحد است؛ اما در سطح شیبدار “الف” به اندازهٔ \(\Large 1\) واحد، در سطح شیبدار “ب” به اندازهٔ \(\Large 2\) واحد و در سطح شیبدار “پ” به اندازهٔ \(\Large3\) واحد به صورت افقی جابهجا شدهایم. حسی هم که نسبت به شیب داریم به ما میگوید که شیب سطح شیبدارهای بالا از چپ به راست کمتر میشود. بنابراین به ازای یک مقدار ثابت جابهجایی در راستای \(\Large y\)، هر چه قدر مقدار جابهجایی در راستای \(\Large x\) بیشتر باشد، شیب کمتر است. در نتیجه میتوانیم بگوییم مقدار شیب با تغییرات عمودی رابطهٔ مستقیم و با تغییرات افقی رابطهٔ معکوس دارد. در قسمت بعدی، با استفاده از مطالبی که در این قسمت بررسی کردیم، تعریف معادلی از شیب ارائه میدهیم.
تعریف دیگری از شیب خط
با توجه به نکاتی که گفتیم، می توانیم شیب خط را به صورت زیر تعریف کنیم:
تعریف شیب خط (با استفاده از نسبت تغییرات): شیب یک خط برابر است با نسبت تغییرات عرضی به طولی دو نقطه از آن خط؛ یعنی اگر \(\Large \begin{bmatrix} x_1 \\ y_1 \end{bmatrix}\) و \(\Large \begin{bmatrix} x_2 \\ y_2 \end{bmatrix}\) دو نقطهٔ دلخواه از خط باشند، شیب خط برابر است با:
\(\LARGE a=\frac{y_1-y_2}{x_1-x_2}\)
برای اینکه بهتر متوجه شوید، به شکل زیر نگاه کنید:
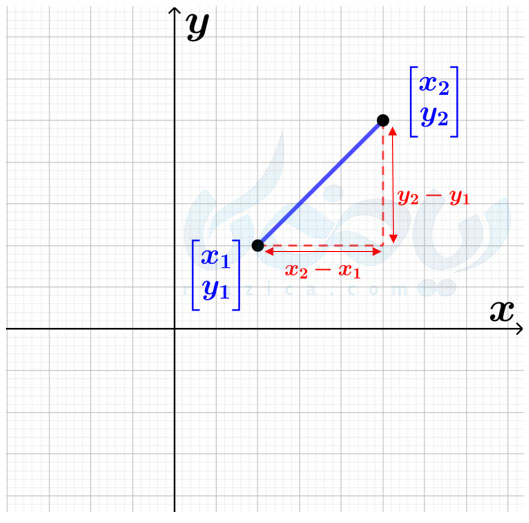
این تعریف و تعریفی که در ابتدای درسنامه ارائه کردیم، یکی هستند. در مثالهای بعدی از درسنامهٔ شیب خط و عرض از مبدا ریاضی نهم میتوانید معادل بودن این دو را ببینید.
مثال از درسنامهٔ شیب خط و عرض از مبدا ریاضی نهم
مثال 1 شیب خط و عرض از مبدا ریاضی نهم: شیب خط زیر را به دست آوردید.
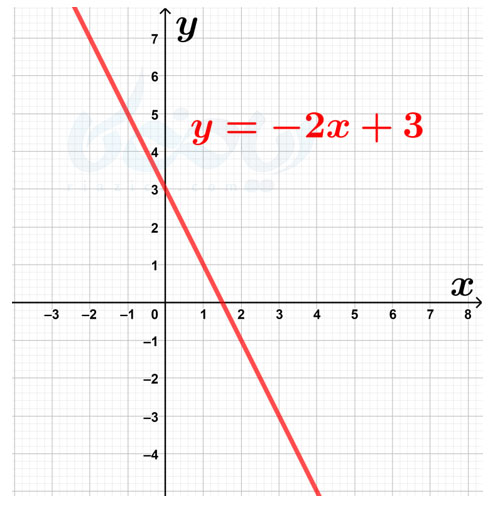
حل: ابتدا دو نقطه را پیدا میکنیم که روی خط قرار داشته باشند. برای این کار میتوانیم از صفحهٔ شطرنجی کمک بگیریم. مثلاً دو نقطهٔ \(\Large \begin{bmatrix} 1 \\ 1 \end{bmatrix}\) و \(\Large \begin{bmatrix} 2 \\ -1 \end{bmatrix}\) که در شکل زیر نیز نشان داده شدهاند، روی خط قرار دارند:
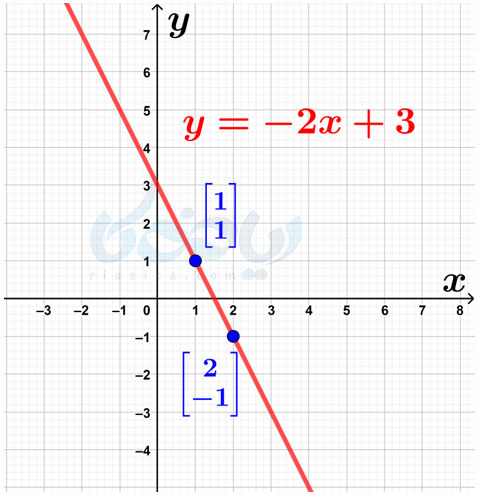
حال کافی است اختلاف \(\Large y\)ها را بر اختلاف \(\Large x\)های این دو نقطه تقسیم کنیم تا شیب به دست بیاید:
\(\LARGE a=\frac{y_1-y_2}{x_1-x_2}=\frac{1-(-1)}{1-2}=-2\)
همان طور که میبینید، عدد به دست آمده برابر با همان ضریب \(\Large x\) در معادله خط شد که توضیح دادیم. بنابراین تفاوتی ندارد که از کدام روش استاده کنیم. در هر صورت به یک جواب میرسیم.
مثال از درسنامهٔ شیب خط و عرض از مبدا ریاضی نهم
مثال 2 شیب خط و عرض از مبدا ریاضی نهم: در شکل زیر، شیب خطوط آبی و قرمز که با یکدیگر موازی هستند را به دست آورید.
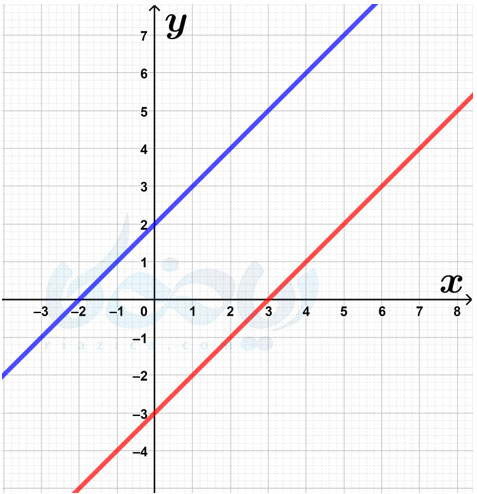
حل: برای به دست آوردن شیب یک خط دیدیدم که دانستن مختصات دو نقطه از آن کافی است (به طور کلی اگر دو نقطه از یک خط را داشته باشیم، تمام اطلاعات آن را داریم). بنابراین ابتدا با توجه به صفحهٔ شطرنجی، مختصات دو نقطه از هر خط را به دست آوریم. در شکل زیر، از هر خط، دو نقطه را مشخص کردهایم:
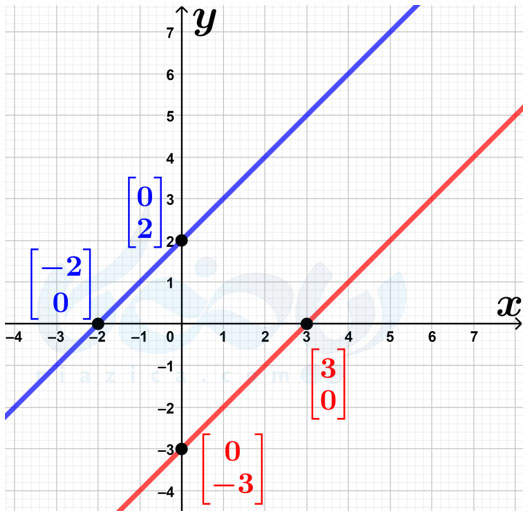
نقاط \(\Large \begin{bmatrix} -2 \\ 0 \end{bmatrix}\) و \(\Large \begin{bmatrix} 0 \\ 2 \end{bmatrix}\) روی خط آبی قرار دارند. بنابراین، اگر شیب خط آبی را با \(\Large a_b\) نشان دهیم، داریم:
\(\LARGE a_b=\frac{2-0}{0-(-2)}=1\)
نقاط \(\Large \begin{bmatrix} 0 \\ -3 \end{bmatrix}\) و \(\Large \begin{bmatrix} 3 \\ 0 \end{bmatrix}\) نیز روی خط قرمز قرار دارند. بنابراین، اگر شیب خط قرمز را با \(\Large a_r\) نشان دهیم، داریم:
\(\LARGE a_r=\frac{0-(-3)}{3-0}=1\)
همان طور که دیدید شیب دو خط با یکدیگر برابر شد. از طرفی دو خط با یکدیگر موازی هستند. به طور کلی خطوط موازی دارای شیبهای برابرند. در قسمت بعدی از درسنامهٔ شیب خط و عرض از مبدا ریاضی نهم به بررسی جزء دوم معادلهٔ خط، یعنی عرض از مبدا میپردازیم.
عرض از مبدا چیست؟
تعریف عرض از مبدا: در معادلهٔ خط \(\Large y=ax+b\) به \(\Large b\) عرض از مبدا میگوییم. عرض از مبدا یک خط در واقع همان عرض محل برخورد خط با محور عرضهاست.
پاسخ به این سؤال که چرا \(\Large b\) در معادلهٔ خط \(\Large y=ax+b\) همان عرض نقطهٔ برخورد خط با محور عرض هاست، بسیار ساده است. کافی است در معادله به جای \(\Large x\) عدد \(\Large 0\) را قرار دهیم. در این صورت مقدار \(\Large y\) برابر با \(\Large b\) خواهد شد. در نتیجه نقطهٔ \(\Large \begin{bmatrix} 0 \\ b \end{bmatrix}\) که روی محور عرضها قرار دارد و یکی از نقاط خط است، همان نقطهٔ تقاطع خط با محور عرضها خواهد شد. به مثال بعدی از درسنامهٔ شیب خط و عرض از مبدا ریاضی نهم توجه کنید.
مثال از عرض از مبدا
مثال 3 شیب خط و عرض از مبدا ریاضی نهم: عرض از مبدا خط به معادلهٔ \(\Large y=\frac{3}{2}x+2\) را به دست آورید.
حل: همان طور که گفتیم، عرض از مبدا خط به معادلهٔ \(\Large y=ax+b\) برابر با \(\Large b\) است. در معادلهٔ \(\Large y=\frac{3}{2}x+2\)، مقدار \(\Large a\) که همان شیب خط است برابر با \(\Large \frac{3}{2}\) و مقدار \(\Large b\) که عرض از مبدا است برابر است با \(\Large 2\). در شکل زیر میتوانید خط \(\Large y=\frac{3}{2}x+2\) را مشاهده کنید:

همان طور که میبینید، در شکل بالا محل تقاطع خط با محور عرضها را که همان نقطهٔ \(\Large \begin{bmatrix} 0 \\ 2 \end{bmatrix}\) است، نشان دادهایم. به مثال بعدی از درسنامهٔ شیب خط و عرض از مبدا ریاضی نهم توجه کنید.
مثال 4 شیب خط و عرض از مبدا ریاضی نهم: عرض از مبدا خط زیر را به دست آورید.
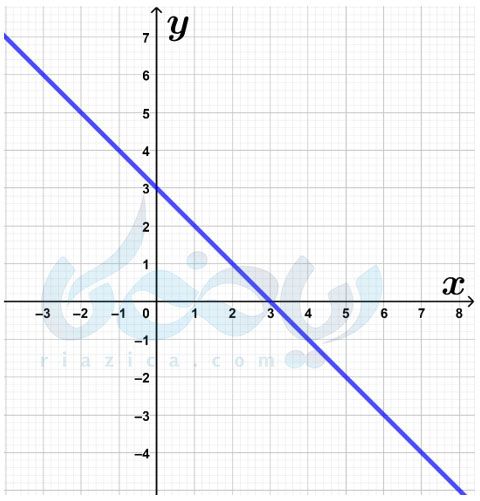
حل: همان طور که گفتیم، عرض از مبدا یک خط همان عرض نقطهٔ برخورد خط با محور عرضهاست. در شکل زیر محل برخورد خط با محور عرضها را که همان نقطهٔ \(\Large \begin{bmatrix} 0 \\ 3 \end{bmatrix}\) است، مشخص کردهایم:
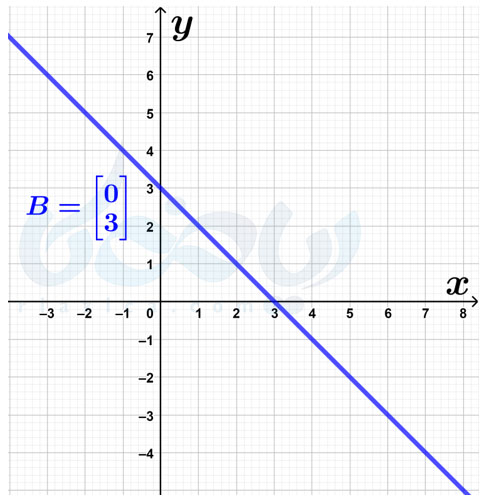
بنابراین، عرض از مبدا خط برابر با \(\Large 3\) است. در قسمت بعدی مثالهای مختلفی از پیدا کردن شیب خط و عرض از مبدا و همچنین نوشتن معادله خط حل خواهیم کرد.
مثال از درسنامهٔ شیب خط و عرض از مبدا ریاضی نهم
مثال 5 شیب خط و عرض از مبدا ریاضی نهم: معادلهٔ خطی را بنویسید که شیب آن برابر با \(\Large 3\) و عرض از مبدا آن برابر با \(\Large -1\) باشد.
حل: اگر معادلهٔ خطی به شکل \(\Large y=ax+b\) داشته باشیم، شیب خط آن برابر با \(\Large a\) و عرض از مبدا آن برابر با \(\Large b\) است. بنابراین کافی است در معادلهٔ \(\Large y=ax+b\) به جای ضرایب \(\Large a\) و \(\Large b\) به ترتیب اعداد \(\Large 3\) و \(\Large -1\) را قرار دهیم تا خط \(\Large y=3x-1\) حاصل شود که همان خواستهٔ مسئله است. در شکل زیر، خط \(\Large y=3x-1\) را رسم کردهایم:
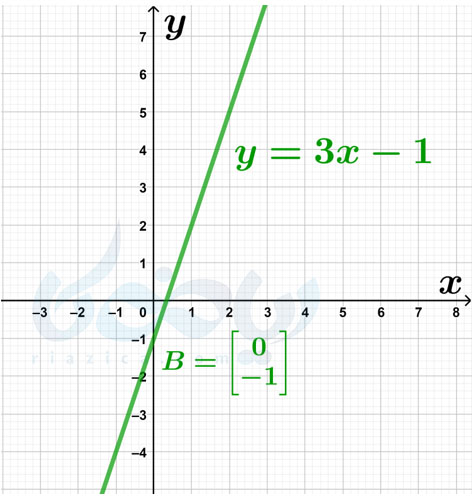
به مثال بعدی از درسنامهٔ شیب خط و عرض از مبدا ریاضی نهم توجه کنید.
مثال از یافتن معادله خط
مثال 6 شیب خط و عرض از مبدا ریاضی نهم: معادلهٔ خطی را بنویسید که با خط \(\Large y=-x+1\) موازی بوده و محور عرضها را در نقطهای به عرض \(\Large 3\) قطع کند.
حل: همان طور که گفتیم، خطوط موازی دارای شیبهای یکسان هستند. شیب خط \(\Large y=-x+1\) برابر با \(\Large -1\) است، بنابراین شیب خطی که قصد داریم معادلهٔ آن را بنویسیم نیز باید \(\Large -1\) باشد. حال باید عرض از مبدا را پیدا کنیم. عرض محل برخورد خط با محور عرضها همان عرض از مبدا خط است. بنابراین باید معادلهٔ خطی با شیب \(\Large -1\) و عرض از مبدا \(\Large 3\) بنویسیم. کافی است در معادلهٔ \(\Large y=ax+b\) به جای \(\Large a\) مقدار \(\Large -1\) و به جای \(\Large b\) مقدار \(\Large 3\) قرار دهیم. در این صورت معادلهٔ خط خواسته شده برابر با \(\Large y=-x+3\) خواهد بود. در شکل زیر، خط \(\Large y=-x+3\) را رسم کردهایم:
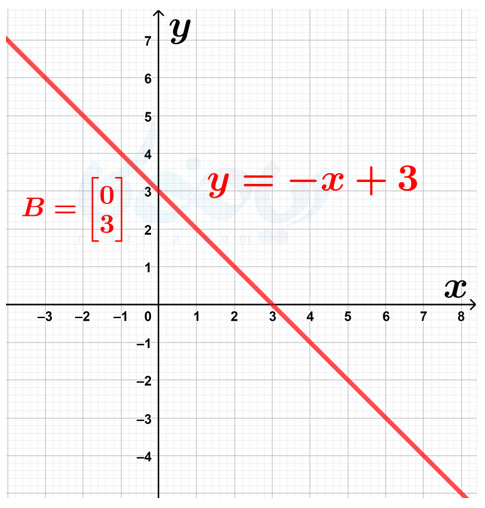
به مثال بعدی از درسنامهٔ شیب خط و عرض از مبدا ریاضی نهم توجه کنید.
مثال از درسنامهٔ شیب خط و عرض از مبدا ریاضی نهم
مثال 7 شیب خط و عرض از مبدا ریاضی نهم: معادلهٔ خط موجود در شکل زیر را بنویسید.
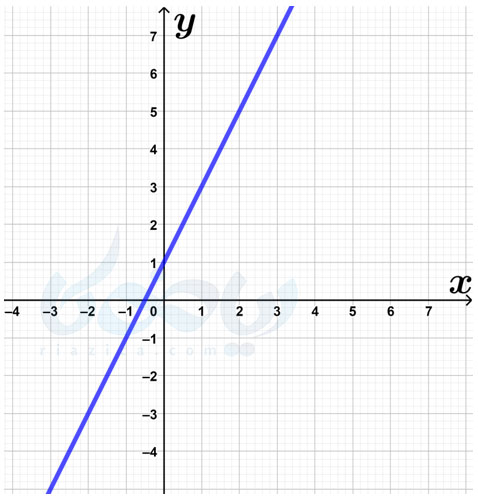
حل: کافی است شیب خط و عرض از مبدا را در شکل بالا به دست آوریم. برای پیدا کردن شیب، کافی است مختصات دو نقطه از خط را به دست آورده و نسبت تغییرات عرض به طول را حساب کنیم. در شکل زیر، دو نقطهٔ \(\Large \begin{bmatrix} -1 \\ -1 \end{bmatrix}\) و \(\Large \begin{bmatrix} 1 \\ 3 \end{bmatrix}\) از خط را مشخص کردهایم:
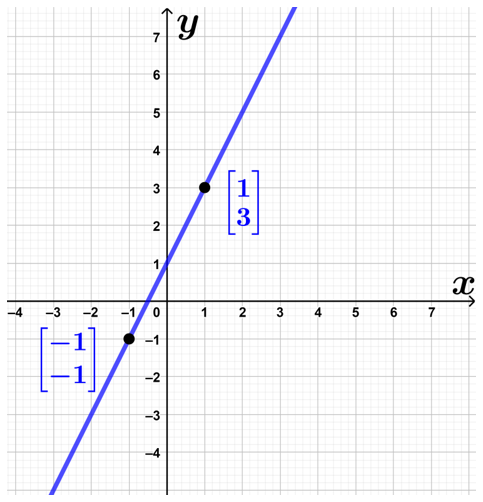
بنابراین، شیب خط برابر است با:
\(\LARGE a=\frac{-1-3}{-1-1}=2\)
برای عرض از مبدا نیز کافی است عرض محل برخورد خط با محور عرضها را مشخص کنیم. در شکل زیر، محل برخورد خط با محور عرضها را که همان نقطهٔ \(\Large \begin{bmatrix} 0 \\ 1 \end{bmatrix}\) است، مشخص کردهایم:
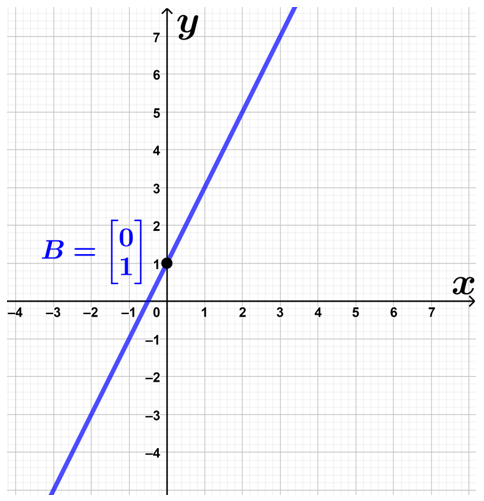
بنابراین عرض از مبدا خط برابر است با \(\Large 1\). شیب خط هم که برابر با \(\Large 2\) شد. در نتیجه، معادلهٔ خط خواسته شده به صورت \(\Large y=2x+1\) است. به مثال بعدی از درسنامهٔ شیب خط و عرض از مبدا ریاضی نهم توجه کنید.
مثال از پیدا کردن معادله خط عبوری از دو نقطه
مثال 8 شیب خط و عرض از مبدا ریاضی نهم: معادلهٔ خط عبوری از دو نقطهٔ \(\Large \begin{bmatrix} -2 \\ 3 \end{bmatrix}\) و \(\Large \begin{bmatrix} 6 \\ -1 \end{bmatrix}\) را بنویسید.
حل: از آنجاییکه دو نقطه از خط را داریم، میتوانیم شیب خط را محاسبه کنیم. شیب خط برابر است با نسبت تغییرات عرض به طول دو نقطهٔ \(\Large \begin{bmatrix} -2 \\ 3 \end{bmatrix}\) و \(\Large \begin{bmatrix} 6 \\ -1 \end{bmatrix}\). در نتیجه شیب خط برابر است با:
\(\LARGE a=\frac{-1-3}{6-(-2)}=-\frac{1}{2}\)
بنابراین معادله خط به صورت \(\Large y=-\frac{1}{2}x+b\) خواهد شد که \(\Large b\) همان عرض از مبدا است و باید آن را به دست آوریم. برای به دست آوردن \(\Large b\) کافی است یکی از نقاط داده شده را در معادله قرار هیم. مثلاً نقطهٔ \(\Large \begin{bmatrix} -2 \\ 3 \end{bmatrix}\) را در معادله قرار میدهیم. یعنی به جای \(\Large x\) مقدار \(\Large -2\) و به جای \(\Large y\) مقدار \(\Large 3\) را جاگذاری میکنیم. در این صورت داریم:
\(\LARGE 3=-\frac{1}{2} \times (-2)+b\)
\(\LARGE \Rightarrow 3=1+b\)
\(\LARGE \Rightarrow b=2\)
بنابراین مقدار \(\Large b\) که همان عرض از مبدا است، برابر با \(\Large 2\) است. در نتیجه معادله خط به صورت \(\Large y=-\frac{1}{2}x+2\) است. در شکل زیر، خط \(\Large y=-\frac{1}{2}x+2\) را رسم کردهایم :
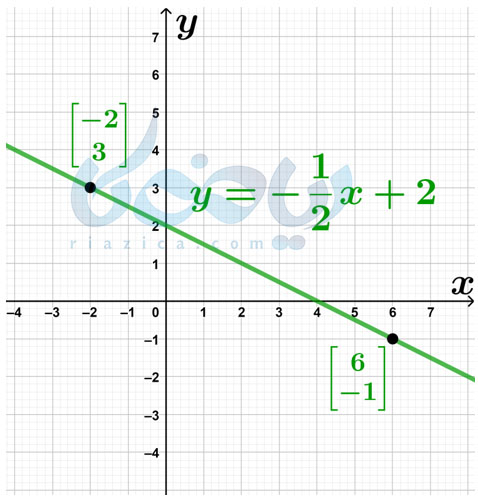
به مبحث بعدی از درسنامهٔ شیب خط و عرض از مبدا ریاضی نهم توجه کنید.
صورت کلی معادلههای خطی
یکی از صورتهای کلی معادلههای خطی در فضای دو بعدی به شکل زیر است:
\(\LARGE ax+by=c\)
دقت کنید که دیگر در معادلهٔ بالا، ضرایب \(\Large a\) و \(\Large b\) شیب خط و عرض از مبدا نیستند. تنها زمانی \(\Large a\) شیب خط و \(\Large b\) عرض از مبدا است که معادلهای به شکل \(\Large y=ax+b\) داشته باشیم. به همین خاطر ابتدا باید معادلهٔ بالا را به شکل \(\Large y=ax+b\) درآوریم تا بتوانیم شیب خط و عرض از مبدا را به دست آوریم. برای این کار، ابتدا دو طرف معادلهٔ بالا را تقسیم بر \(\Large b\) کرده و سپس \(\Large x\) و ضریبش را به سمت راست میبریم:
\(\LARGE ax+by=c\)
\(\LARGE \Rightarrow \frac{ax+by}{b}=\frac{c}{b}\)
\(\LARGE \Rightarrow \frac{a}{b}x+y=\frac{c}{b}\)
\(\LARGE \Rightarrow y=-\frac{a}{b}x+\frac{c}{b}\)
در این حالت، ضریب \(\Large x\) که همان \(\Large -\frac{a}{b}\) است، برابر است با شیب خط و \(\Large \frac{c}{b}\) برابر است با عرض از مبدا. میتوانید در مسائل دیگر بدون انجام محاسبات بالا از نتایجی که به دست آوردیم استفاده کنید.
برعکس این کار را نیز میتوانیم انجام دهیم. یعنی اگر معادلهٔ خطی به صورت بالا نبود، میتوانیم آن را به صورت بالا بنویسیم. برای اینکه یک معادله خط به شکل بالا درآید، لازم است متغیرهای \(\Large x\) و \(\Large y\) را به همراه ضرایبشان به یک طرف تساوی برده و عدد ثابت را در یک طرف تساوی نگه داریم. به طور مثال اگر بخواهیم خط \(\Large y=2x-3\) را به شکل بالا بنویسیم، \(\Large 2x\) را قرینه کرده و به طرف چپ تساوی میبریم و \(\Large -3\) را سمت راست تساوی نگه میداریم تا معادله به شکل \(\Large -2x+y=-3\) در آید. در این صورت، مقدار \(\Large a\) در معادلهٔ \(\Large -2x+y=-3\) برابر با \(\Large -2\)، مقدار \(\Large b\) برابر با \(\Large 1\) و مقدار \(\Large c\) برابر با \(\Large -3\) خواهد بود. به مثال بعدی از درسنامهٔ شیب خط و عرض از مبدا ریاضی نهم توجه کنید.
مثال از صورت کلی معادلههای خطی
مثال 9 شیب خط و عرض از مبدا ریاضی نهم: شیب خط و عرض از مبدا خط به معادلهٔ \(\Large 6x+3y=9\) را بیابید.
حل: هم میتوانیم از نتایجی که به دست آوردیم استفاده کنیم و هم میتوانیم معادلهٔ داده شده را به شکل \(\Large y=ax+b\) در آورده و شیب خط و عرض از مبدأ را پیدا کنیم. روش دوم را انتخاب میکنیم تا ساده سازی معادلات را هم تمرین کرده باشیم:
\(\LARGE 6x+3y=9\)
\(\LARGE \Rightarrow \frac{6x+3y}{3}=\frac{9}{3}\)
\(\LARGE \Rightarrow 2x+y=3\)
\(\LARGE \Rightarrow y=-2x+3\)
حال که معادله به شکل \(\Large y=ax+b\) در آمد، ضریب \(\Large x\) که همان \(\Large -2\) است برابر با شیب و \(\Large 3\) برابر با عرض از مبدا است. به مبحث بعدی از درسنامهٔ شیب خط و عرض از مبدا ریاضی نهم توجه کنید.
معادلهٔ محور طولها و محور عرضها
همان طور که گفتیم، یکی از صورتهای کلی معادلهٔ خط به شکل \(\Large ax+by=c\) است. اگر در این معادله، مقدار \(\Large a\) و \(\Large c\) را برابر با صفر و مقدار \(\Large b\) را برابر با \(\Large 1\) قرار دهیم، معادله خط به صورت \(\Large y=0\) در میآید که همان معادلهٔ محور طولهاست. در واقع تمام نقاطی که روی محور طولها قرار دارند دارای عرض صفر هستند. اگر مقدار \(\Large b\) و \(\Large c\) را برابر با \(\Large 0\) و مقدار \(\Large a\) را برابر با \(\Large 1\) قرار دهیم، معادلهٔ محور عرضها به دست میآید. در واقع تمام نقاطی که روی محور عرضها قرار دارند دارای طول صفر هستند.
به طور کلی معادلاتی به شکل \(\Large y=c\)، معادلات خطوط ثابت هستند. از تلاقی خطوط ثابت با خطوطی به شکل \(\Large x=c’\)، یک نقطه به وجود میآید. مثلاً، دو خط \(\Large y=0\) و \(\Large x=0\) که همان محور طولها و محور عرضها هستند، یکدیگر را در مبدا مختصات قطع میکنند. یا به طور مثال، دو خط \(\Large y=2\) و \(\Large x=-1\) یکدیگر را در نقطهٔ \(\Large \begin{bmatrix} -1 \\ 2 \end{bmatrix}\) قطع میکنند. زیرا این نقطه دارای طول \(\Large -1\) و عرض \(\Large 2\) است. در شکل زیر میتوانید دو خط \(\Large x=c_1\) و \(\Large y=c_2\) و نقطهٔ برخورد آنها را مشاهده کنید:
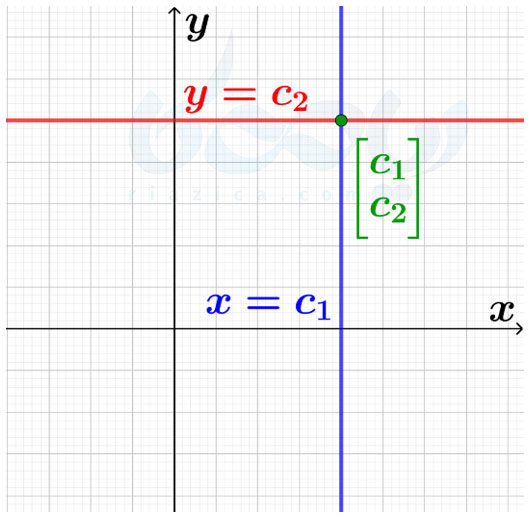
همان طور که در شکل بالا هم میبینید، خطوط \(\Large x=c\) همیشه موازی با محور عرضها و خطوط \(\Large y=c\) همیشه موازی با محور طولها هستند.
زنگ آخر کلاس شیب خط و عرض از مبدا ریاضی نهم
در درسنامهای که از ریاضی نهم خواندیم، ابتدا توضیح دادیم منظور از شیب خط چیست. روش به دست آوردن شیب یک خط با دانستن مختصات دو نقطه از آن را بررسی کردیم. سپس، به معرفی عرض از مبدا پرداختیم. همان طور که دیدید، عرض از مبدا یک خط برابر بود با عرض نقطهٔ برخورد خط با محور عرضها. در انتهای درسنامه نیز، صورت کلی معادله خط را بررسی کردیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با شیب خط و عرض از مبدا ریاضی نهم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





خیلی ممنون از زحمات شماا
با سلام واحترام
ممنون از شما دوست عزیز
خیلی عالی بود ممنون
با سلام ووقت به خیر
خوشحالیم استفاده بردید
مطالب خیلی مفید بود
خیلی ممنون?
با سلام
ممنون از نظرات خوب شما
سلام لطفا طول از مبدا رو هم بگید و اینکه اگه در معادله ای علاوه بر ایکس و وای ما N یا M داشتیم و گفته بود عرض از مبدا رو بدست بیارید چی کار کنیم
با سلام وعرض ادب
اگه طول از مبدا رو بخواهیم به جای وای صفر میگذاریم وایکس رو پیدا میکنیم
اگه غیر از طول وعرض مجهول دیگه ای داشته باشیم باید با توجه به داده های مسئله عرض از مبدارو پیدا کنیم
سلام یک سوال ریاض دارم
خطی از نقطه (۳،۲)گذشته است و عرض مبدا آن ۵ است، ضریب زاویه خط چقدر است؟؟
با سلام و عرض ادب
کافیه در معادله خط مختصات این نقطه رو به جای x,y بذارید و به جای b هم عرض از مبدا رو بذارید وشیب یا همون ضریب زاویه خط به دست بیاد
سلام و خسته نباشید خدمت شما و تشکر از سایت خوبتون
بنده فکر میکنیم این جمله که در زیر عکس دوم از سه مثلث نوشته شده غلطه: ″بنابراین به ازای یک مقدار ثابت جابهجایی در راستای y، هر چه قدر مقدار جابهجایی در راستای x بیشتر باشد، شیب بیشتر است.″ در واقع با ثابت بودن جابجایی در محور y هر چه قدر جابجایی در محور x بیشتر بشه شیب کمتره و فکر میکنم عکس هم اشتباه ترسیم شده و در واقع فلش بایستی معکوس بشه.
با سلام وقت به خیر
ممنون از دقت نظرشماتصحیح میشود
سلام خیلی ممنون بسیار مفید بود
با سلام واحترام
ممنون از نظر لطف شما
واقعا دلیل این که چرا برای فرمول شیب ، دلتا y را به دلتا x تقسیم میکنیم عالی توضیح دادین ( دلیل این که شیب با تغییرات y رابطه مستقیم و با تغییرات x رابطه عکس دارد عالی توضیح دادین . در واقع تو هیچ سایتی و کتابی توضیحاتی به این روشنی نداده بود ) فقط یه اشتباه تایپی تو نوشته هاتون هست که لطفا اصلاح فرمایید ؛ perfect ?
با سلام وعرض ادب
ممنون از لطف وانرژی مثبت شما اصلاح خواهد شد
عالی دست شما درد نکنه
سلامت باشید دوست عزیز
واقعا عالی بود.
با سلام واحترام
خدا روشکر که مفید واقع شده
عالی بود.
با سلام و ادب
ممنون دوست عزیز
عالی بود ممنون دوست عزیز?
سلام مطالب بسیار مفیدی بود تشکر