اکسترمم نسبی ، یکنوایی، نقطه ی بحرانی 📸👣 ریاضی دوازدهم تجربی – گام به گام با تصویر

در این درسنامه به سه مبحث مهم خواهیم ‌پرداخت. ابتدا یکنوایی توابع را بررسی می‌کنیم. سپس توضیح خواهیم‌ داد که نقاط بحرانی توابع، چه نقاطی هستند. در انتها نیز اکسترمم نسبی را معرفی خواهیم‌کرد.

آزمون یکنوایی

هدف آزمون یکنوایی این است که با بررسی علامت مشتق تابع در یک بازه، صعودی، نزولی و یا ثابت بودن تابع را در آن بازه تعیین کند. اما علامت مشتق تابع، چه ارتباطی با صعودی‌ بودن، نزولی بودن و یا ثابت بودن تابع در یک بازه دارد؟ همان‌طور که می‌دانید، مشتق تابع در یک نقطه برابر است با شیب خط مماس بر نمودار تابع در آن نقطه. تابع \(\Large  f(x) \) که نمودار آن در شکل زیر رسم شده است را در نظر بگیرید:

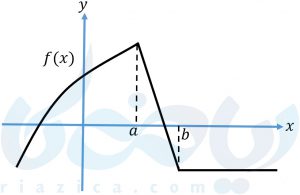
همان طور که در شکل بالا می‌بینید، در بازهٔ \(\Large  (-\infty, a) \)، شیب خط مماس بر نمودار مثبت است. تابع نیز در این بازه اکیداً صعودی است. در بازه‌ٔ \(\Large  (a, b) \)، شیب خط مماس بر نمودار منفی است و تابع اکیداً نزولی است. نهایتاً، در بازهٔ \(\Large  (b, \infty) \)، تابع ثابت است و شیب خط مماس بر نمودار صفر خواهد بود. احتمالاً خودتان ارتباط بین علامت مشتق تابع و صعودی، نزولی و یا ثابت بودن تابع در یک بازه را یافته‌اید. به طور خلاصه وضعیت یکنوایی تابع در یک بازه را می‌توان با استفاده از جدول زیر مشخص کرد:

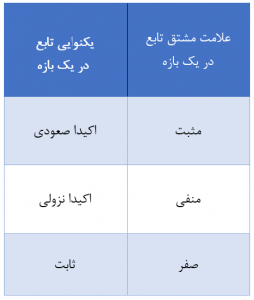
بنابراین در صورت دانستن ضابطهٔ یک تابع کافی است ابتدا مشتق آن را به دست آوریم. سپس با تعیین علامت تابع مشتق و با استفاده از جدول بالا، وضعیت یکنوایی تابع در هر بازه را مشخص کنیم. برای مرور چگونگی تعیین علامت تابع می‌توانید به درسنامه‌ی تعیین علامت عبارت‌های جبری در آموزش پایه‌ی دهم مراجعه کنید.

مثال 1: تابع \(\Large  f(x)=2x^3-6x \) در چه بازه‌هایی اکیدا صعودی و در چه بازه هایی اکیدا نزولی است؟

حل: همان‌طور که گفتیم، ابتدا باید مشتق تابع را محاسبه کنیم:

\(\LARGE  f(x)=2x^3-6x \)

\(\LARGE \Rightarrow f'(x)=6x^2-6 \)

حال باید \(\Large  f'(x) \) را تعیین علامت کنیم. برای تعیین علامت \(\Large  f'(x) \)، لازم است ریشه‌های آن را به دست آوریم:

\(\LARGE  f'(x)=0 \)

\(\LARGE \Rightarrow 6x^2-6=0 \)

\(\LARGE \Rightarrow x^2=1\)

\(\LARGE \Rightarrow x=-1, 1\)

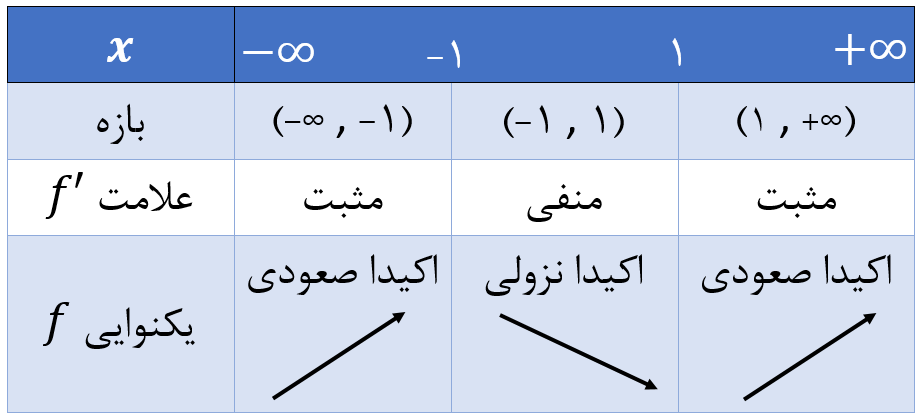
بنابراین علامت \(\Large  f'(x) \) و وضعیت یکنوایی \(\Large  f(x) \) در بازه‌های مختلف، به صورت زیر در می‌آید:

نقاط بحرانی تابع

تعریف مهم دیگری که باید در مبحث اکسترمم نسبی با آن آشنا شویم نقاط بحرانی است. هرگاه مشتق تابع در یک نقطه وجود نداشته ‌باشد، و یا وجود داشته ‌باشد ولی صفر باشد، به آن نقطه از دامنهٔ تابع، نقطه بحرانی می‌گوییم. به مثال زیر دقت کنید.

مثال 2: نمودار تابع \(\Large  f(x) \) در شکل زیر رسم شده است. نقاط بحرانی \(\Large  f \) را مشخص کنید.

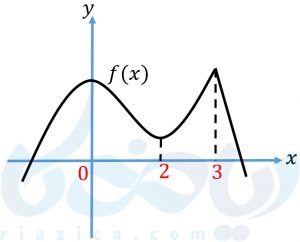
حل: همان‌طور که در شکل بالا پیداست، مشتق تابع در نقاط \(\Large  x=0 \) و \(\Large  x=2 \) برابر با صفر است. در نقطه‌ٔ \(\Large  x=3 \)، مشتق چپ و راست برابر نیست. بنابراین، مشتق \(\Large  f \) در نقطه‌ٔ \(\Large  x=3 \) وجود ندارد. پس طبق تعریف نقطه بحرانی، نقاط \(\Large  x=2 \) ،\(\Large  x=0 \) و \(\Large  x=3 \) نقاط بحرانی تابع \(\Large  f(x) \) هستند.

اکسترمم نسبی

اکسترمم نسبی را می‌توان به دو دستهٔ اصلی تقسیم‌بندی کرد:

1. ماکزیمم نسبی
2. مینیمم نسبی

اما منظور از این دو چیست؟ در ادامه مبحث اکسترمم نسبی ابتدا تعریف آن‌ها را می بینیم. سپس، با حل چند مثال، درک بهتری از موضوع پیدا خواهیم‌کرد.

ماکزیمم نسبی

می‌گوییم تابع \(\Large  f \) در نقطه‌ای مثل \(\Large  a \) دارای ماکزیمم نسبی است، هرگاه یک همسایگی از \(\Large  a \) در دامنه‌ٔ تابع وجود داشته باشد. به طوری که مقدار تابع در \(\Large  x=a \) از مقدار تابع در هر نقطه‌ٔ دیگر از آن همسایگی بیشتر باشد. در این حالت، به مقدار \(\Large  f(a) \) نیز ماکزیمم نسبی تابع می‌گوییم. شاید این تعریف کمی پیچیده به نظر برسد. برای روشن شدن مطلب، نمودار تابع \(\Large  f \) که در شکل زیر رسم شده است را در نظر بگیرید:

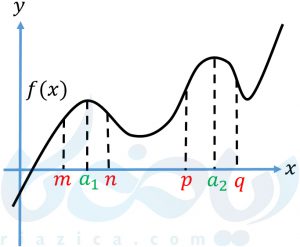
برای \(\Large  x=a_1 \)، یک همسایگی مثل بازهٔ \(\Large  (m, n) \) وجود دارد که مقدار تابع در \(\Large  x=a_1 \) از مقدار تابع در هر نقطه‌ی دیگر این همسایگی بیشتر است. برای نقطه‌ٔ \(\Large  x=a_2 \) نیز، یک همسایگی مثل \(\Large  (p, q) \) وجود دارد که مقدار تابع در \(\Large  x=a_2 \) از مقدار تابع در هر نقطه‌ٔ دیگر این همسایگی بیشتر است. بنابراین، تابع \(\Large  f \) در نقاط \(\Large  x=a_1 \) و \(\Large  x=a_2 \) دارای ماکزیمم نسبی است و مقادیر این ماکزیمم‌‌های نسبی به ترتیب برابر با \(\Large  f(a_1) \) و \(\Large  f(a_2) \) هستند.

مینیمم نسبی

اکسترمم نسبی دیگری که مورد بررسی قرار می‌دهیم مینیمم نسبی است. می‌گوییم تابع \(\Large  f \) در نقطه‌ای مثل \(\Large  b \) دارای مینیمم نسبی است. هرگاه یک همسایگی از \(\Large  b \) در دامنه‌ٔ تابع وجود داشته باشد به طوری که مقدار تابع در \(\Large  x=b \) از مقدار تابع در هر نقطه‌ٔ دیگر آن همسایگی کمتر باشد. در این حالت، به مقدار \(\Large  f(b)\) نیز مینیمم نسبی تابع می‌گوییم. نمودار تابع \(\Large  f \) که در شکل زیر رسم شده است را در نظر بگیرید:

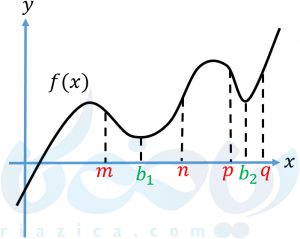
برای \(\Large  x=b_1 \)، یک همسایگی مثل بازه‌ٔ \(\Large  (m, n)\) وجود دارد که مقدار تابع در \(\Large  x=b_1 \) از مقدار تابع در هر نقطه‌ٔ دیگر این همسایگی کمتر است. برای نقطه‌ٔ \(\Large  x=b_2 \) نیز، یک همسایگی مثل \(\Large  (p, q) \) وجود دارد که مقدار تابع در \(\Large  x=b_2 \) از مقدار تابع در هر نقطه‌ٔ دیگر این همسایگی کمتر است. بنابراین، تابع \(\Large  f \) در نقاط \(\Large  x=b_1 \) و \(\Large  x=b_2 \) دارای مینیمم نسبی است و مقادیر این مینیمم‌های نسبی به ترتیب برابر با \(\Large  f(b_1) \) و \(\Large  f(b_2) \) هستند.

آزمون مشتق اول

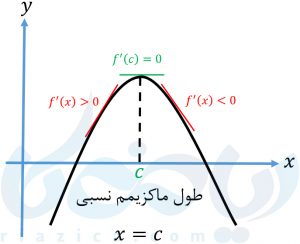
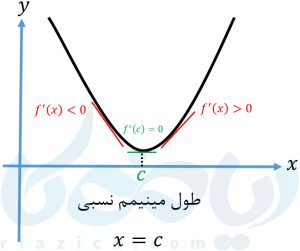
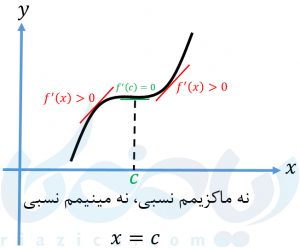
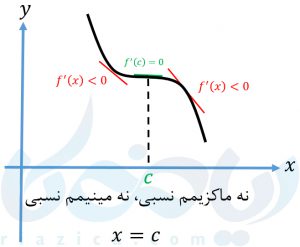
پیدا کردن اکسترمم‌های نسبی (ماکزیمم نسبی و مینیمم نسبی) از روی نمودار ساده است. اما اگر ضابطه‌ٔ تابع را داشته باشیم باید چه کار کنیم؟ در این حالت برای پیدا کردن اکسترمم نسبی از آزمون مشتق اول استفاده می‌کنیم. برای انجام این آزمون، ابتدا نقاط بحرانی تابع \(\Large  f \) را که تابع در آن‌ها پیوسته بوده و در یک همسایگی محذوف آن مشتق‌پذیر است پیدا می‌کنیم. اگر علامت \(\Large  f’ \) در آن نقطه، از مثبت به منفی تغییر کند، تابع در آن نقطه دارای ماکزیمم نسبی است. اگر علامت \(\Large  f’ \) در آن نقطه، از منفی به مثبت تغییر کند، تابع در آن نقطه دارای مینیمم نسبی است. در غیر از این دو صورت، اکسترمم نسبی نداریم. برای درک بهتر، در چهار نمودار زیر، حالات ممکن را بررسی کرده‌ایم:

چند مثال از اکسترمم نسبی

مثال 3: اکسترمم های نسبی تابع \(\Large  f(x)=x^3+3x^2-9x+4 \) را در صورت وجود بیابید.

حل: ابتدا باید نقاط بحرانی تابع \(\Large  f \) را پیدا کنیم:

\(\LARGE f'(x)=3x^2+6x-9\)

\(\LARGE f'(x)=0\)

\(\LARGE \Rightarrow x=-3, 1\)

حال باید \(\Large  f'(x) \) را تعیین علامت کنیم:

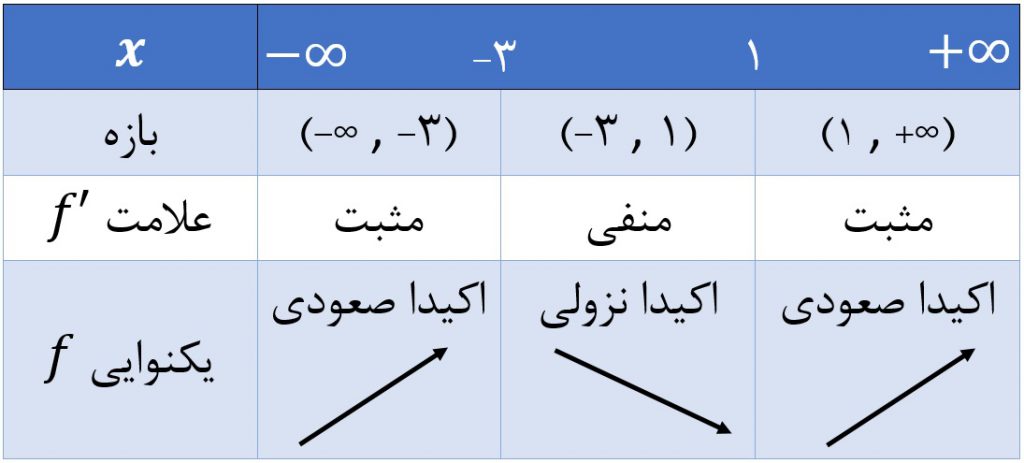
همان‌طور که می‌بینید، \(\Large  f’ \) در \(\Large  x=-3 \) از مثبت به منفی تغییر علامت داده است. پس، \(\Large  f \) در \(\Large  x=-3 \) ماکزیمم نسبی دارد. مقدار این ماکزیمم برابر با \(\Large  f(-3)=31 \) است. علاوه‌ بر این، \(\Large  f’ \) در \(\Large  x=1 \) از منفی به مثبت تغییر علامت می‌دهد. پس \(\Large  f \) در \(\Large  x=1 \) مینیمم نسبی دارد و مقدار این مینیمم نسبی برابر است با \(\Large  f(1)=-1 \).

مثال 4: اکسترمم های نسبی تابع \(\Large  g(x)=-x^3-3x+2 \) را در صورت وجود تعیین کنید.

حل: ابتدا باید نقاط بحرانی تابع \(\Large  g \) را تعیین کنیم:

\(\LARGE g'(x)=-3x^2-3\)

\(\LARGE g'(x)=0\)

\(\LARGE \Rightarrow x^2=-1\)

اما معادله‌ٔ بالا در مجموعه‌ٔ اعداد حقیقی جوابی ندارد. بنابراین تابع \(\Large  g(x) \) نقطهٔ بحرانی نداشته و در نتیجه اکسترمم نسبی ندارد.

مثال 5: اکسترمم‌ های نسبی تابع \(\Large  h(x)=x^3+4 \) را در صورت وجود بیابید.

حل: ابتدا نقاط بحرانی تابع را پیدا می‌کنیم:

\(\LARGE h'(x)=3x^2\)

\(\LARGE h'(x)=0\)

\(\LARGE \Rightarrow x=0\)

در نتیجه، \(\Large  x=0 \) نقطه‌ بحرانی \(\Large  h(x) \) است. حال باید \(\Large  h'(x) \) را تعیین علامت کنیم:

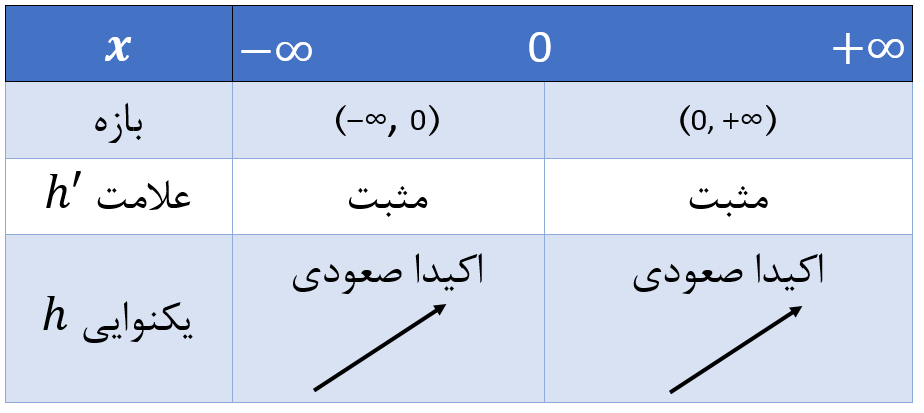
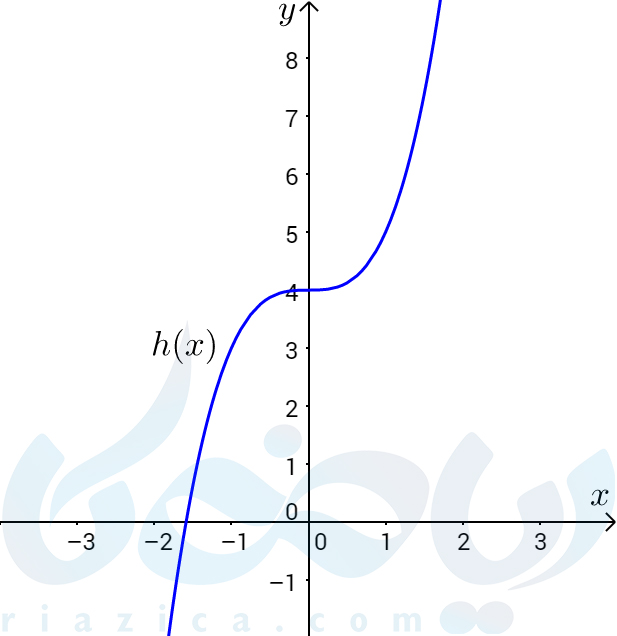
همان طور که می‌بینید، \(\Large  h'(x) \) در نقطه‌ٔ \(\Large  x=0 \) تغییر علامت نداده است. در نتیجه \(\Large  h \)، اکسترمم نسبی ندارد. برای اینکه شهود بهتری پیدا کنید، به نمودار \(\Large  h(x) \) که در شکل زیر رسم شده است نگاه کنید. همان طور که می‌بینید، با اینکه شیب خط مماس بر نمودار در نقطه‌ی \(\Large  x=0 \)، صفر شده، ماکزیمم یا مینیمم نسبی وجود ندارد.

در ادامه مطلب حتما پست اکسترمم مطلق ریاضی دوازدهم رومطالعه کنید.

زنگ آخر کلاس یکنوایی، نقطه بحرانی و اکسترمم نسبی

در درسنامه‌ای که خواندیم به سه مبحث مهم پرداخته ‌شد.

1. ابتدا یکنوایی توابع را بررسی کردیم. برای بررسی یکنوایی تابع در بازه‌های مختلف از علامت مشتق تابع در آن بازه ها استفاده می‌کنیم.
2. در قدم بعد، نقاط بحرانی را تعریف کردیم. مشتق تابع در نقاط بحرانی یا وجود ندارد و یا در صورت وجود برابر با صفر است.
3. در مبحث آخر نیز به بررسی اکسترمم نسبی پرداختیم.

ما در ریاضیکا آماده‌ی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث یکنوایی، نقطه ی بحرانی و اکسترمم نسبی‌ پایهٔ دوازدهم تجربی دارید، در دیدگاه‌ها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند ‌داد.