آموزش ریاضی پایه دوازدهم تجربی
آهنگ تغییر ریاضی دوازدهم ⏳⏰ – یادگیری از طریق حل مثال
آهنگ تغییر چیست؟ در کجا کاربرد دارد؟ و چرا استفاده از آن در ریاضیات پایه دوازدهم تجربی مهم است؟ در این درسنامه به آهنگ تغییر ریاضی دوازدهم خواهیم پرداخت. دو نوع آهنگ تغییر داریم:
- آهنگ تغییر متوسط
- آهنگ تغیر لحظه ای
ابتدا هر یک را تعریف میکنیم. سپس با کاربرد آنها در علوم تجربی آشنا خواهیم شد.
تعریف آهنگ تغییر ریاضی دوازدهم
در علوم تجربی در برخی از موارد لازم است تا نسبت تغییر یک کمیت به زمانی که کمیت در آن تغییر کرده را بیابیم. مثلاً در محاسبهٔ سرعت متوسط یک جسم، مقدار تغییر مکان را تقسیم بر زمانی می کنیم که آن جسم طی کرده است. آهنگ تغییر، اندازهٔ این نسبتها را برای ما محاسبه میکند. اگر نسبت تغییرات را به طول یک بازهٔ زمانی بسنجیم، آهنگ متوسط تغییر را محاسبه کردهایم. به عبارت دقیقتر، آهنگ متوسط تغییر یک تابع در بازهٔ \(\Large [a, a+h] \) به صورت زیر تعریف میشود:

اگر در عبارت بالا \(\Large h \) را به سمت صفر میل دهیم و حاصل حد را حساب کنیم، آهنگ تغییر لحظه ای در نقطهٔ \(\Large a \) به دست میآید. بنابراین، آهنگ تغییر لحظه ای تابع \(\Large f \) در نقطهٔ \(\Large x=a \) برابر است با:

همان طور که از عبارت بالا پیداست، آهنگ تغییر لحظه ای تابع \(\Large f \) در نقطهٔ \(\Large x=a \) برابر است با مشتق تابع \(\Large f \) در نقطهٔ \(\Large x=a \)، یعنی \(\Large f'(a) \). انتظار این اتفاق را هم داشتیم. زیرا در محاسبهٔ آهنگ تغییر لحظه ای، اختلاف تابع در دو نقطهٔ نزدیک به هم را تقسیم بر اختلاف این دو نقطه روی محور \(\Large x \) می کنیم. در نتیجه، بنابر مفهوم مشتق، آهنگ تغییر لحظه ای برابر است با شیب خط مماس (اگر مفهوم مشتق را فراموش کرده اید، درسنامهٔ آموزش مشتق دوازدهم تجربی را مرور کنید). آهنگ متوسط تغییر نیز برابر است با شیب خط واصل بین دو نقطه. در ادامه مثالهایی از آهنگ تغییر ریاضی دوازدهم خواهیم دید.
مثال از آهنگ تغییر ریاضی دوازدهم
مثال 1: ساعت شنی از دو حباب تشکیل شده است. حجم حباب بالایی 500 سانتی متر مکعب است. در لحظهٔ \(\Large t=0 \) شن از حباب بالایی شروع به ریختن در حباب پایینی میکند. اگر حجم شن باقی مانده در حباب بالایی پس از \(\Large t \) ثانیه از رابطهٔ زیر به دست آید، در چه زمانی آهنگ تغییر لحظه ای حجم برابر با آهنگ تغییر متوسط آن در بازهٔ \(\Large [0,10] \) میشود؟
\(\LARGE V=500(1-\frac{t}{10})^2 \)
حل ۱: آهنگ تغییر متوسط در بازه \(\Large [0,10] \)، طبق تعریف برابر است با:
\(\LARGE \frac{V(10)-V(0)}{10-0}\)
\(\LARGE =\frac{0-500}{10-0} \)
\(\LARGE =-50 \)
باید ببینیم در چه زمانی آهنگ تغییر لحظه ای برابر با 50- میشود. آهنگ تغییر لحظه ای حجم در ثانیهٔ \(\Large t \)، طبق تعریف برابر است با مشتق تابع حجم. یعنی برابر است با:
\(\Large V'(t)=500 \times 2 \times (\frac{t}{10}-1)\)
\(\LARGE =100t-1000\)
\(\LARGE V'(t)=-50\)
\(\LARGE \Rightarrow 100t-1000=-50\)
\(\LARGE \Rightarrow 100t=950\)
\(\LARGE \Rightarrow t=9.5\)
سرعت متوسط و سرعت لحظه ای
در مبحث آهنگ تغییر ریاضی دوازدهم ، از آهنگ تغییر برای محاسبهٔ سرعت نیز استفاده میکنیم. سرعت متوسط یک جسم در یک بازهٔ زمانی برابر است با آهنگ متوسط تغییر مکان جسم در آن بازه. سرعت لحظه ای یک جسم در یک لحظه نیز برابر است با آهنگ لحظه ای تغییر مکان جسم در آن لحظه.
مثال 2: معادلهٔ حرکت جسمی به صورت \(\Large f(t)=-t^2+4t-3 \) بر حسب متر در بازهٔ زمانی \(\Large [0,5] \) ثانیه است. اگر در لحظهٔ \(\Large t=1 \) جسم شروع به حرکت کند، چند ثانیه بعد از شروع حرکت، سرعت متوسط جسم از آغاز برابر با صفر میشود؟ در آن لحظه، سرعت لحظه ای چه قدر است؟
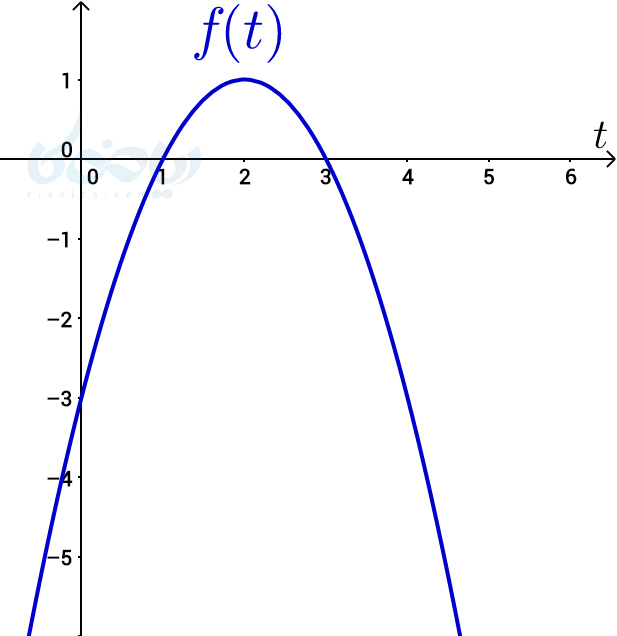
حل: سرعت متوسط جسم از آغاز حرکت تا لحظهٔ \(\Large t \) برابر است با:
\(\LARGE \frac{f(t)-f(1)}{t-1} \)
\(\LARGE =\frac{-t^2+4t-3-0}{t-1} \)
\(\LARGE =\frac{-(t-1)(t-3)}{t-1} \)
\(\LARGE =-t+3 \)
در نتیجه در لحظهٔ \(\Large t=3 \) ثانیه، سرعت متوسط جسم برابر با صفر میشود. طبق تعریف، سرعت لحظه ای در \(\Large t=3 \) ثانیه برابر است با:
\(\LARGE f'(t)=-2t+4 \)
\(\LARGE \Rightarrow f'(3)=-6+4=-2 \)
آهنگ رشد
در مبحث آهنگ تغییر ریاضی دوازدهم ، از مفهوم آهنگ تغییر برای محاسبهٔ آهنگ رشد موجودات زنده نیز استفاده میکنیم. به طور مثال آهنگ رشد یک نوزاد یا آهنگ رشد یک توده باکتری.
مثال 3: جرم یک توده باکتری پس از \(\Large t \) ساعت، از رابطهٔ زیر به دست میآید. آهنگ متوسط رشد این توده باکتری در بازهٔ زمانی \(\Large [1, 4] \) ساعت چه قدر است؟ آهنگ لحظه ای رشد این توده را در لحظهٔ \(\Large t=1 \) به دست آورید.
\(\Large m(t)=4t^3+2t^2+2t+\sqrt{t} \)
حل: طبق تعریف، آهنگ متوسط رشد این توده باکتری در بازهٔ زمانی \(\Large [1, 4] \) برابر است با:
\(\LARGE \frac{m(4)-m(1)}{4-1} \)
\(\LARGE =\frac{298-9}{3} \)
\(\LARGE =91 \)
آهنگ لحظه ای تغییر جرم توده در لحظهٔ \(\Large t=1 \) برابر است با:
\(\Large f'(t)=12t^2+4t+2+\frac{1}{2\sqrt{t}} \)
\(\Large f'(1)=12+4+2+\frac{1}{2}=18.5\)
در ادامه توصیه میشه پست اکسترمم نسبی ،یکنوایی ،نقاط بحرانی ریاضی دوازدهم رو حتما مطالعه کنید.
زنگ آخر کلاس آهنگ تغییر ریاضی دوازدهم
در این درسنامه به معرفی آهنگ تغییر ریاضی دوازدهم پرداختیم. همان طور که گفتیم، دو نوع آهنگ تغییر داریم. آهنگ تغییر متوسط و آهنگ تغییر لحظه ای. آهنگ تغییر متوسط برابر بود با شیب خط واصل بین دو نقطه. آهنگ تغییر لحظه ای برابر بود با مشتق تابع در یک نقطه یا همان خط مماس بر نمودار تابع. همان طور که دیدیم از آهنگ تغییر برای محاسبهٔ سرعت متوسط و لحظه ای و آهنگ رشد موجودات زنده استفاده میشود.
ما در ریاضیکا آمادهٔ هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث آهنگ تغییر ریاضی دوازدهم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





سلام و عرض ادب درحسابان ۲ و در تمرینات آخر فصل سوالی مطرح شده که درستی یا نادرستی آن بایستی مشخص شود،همکاران معتقدند که صعودی بودن برای آهنگ تغییر متوسط تابع بی معنی بوده و قابل تعریف نیست،بنده معتقدم که آهنگ تغییر متوسط تابع هم می تواند صعودی،نزولی و ثابت باشد،ممنون میشم اعلام نظر بفرمائید.