پاسخنامه تشریحی سوالات ریاضی تیزهوشان نهم ۹۸-۹۹ 📸📕!

در این صفحه پاسخنامه تشریحی سوالات ریاضی تیزهوشان نهم ۹۸-۹۹ را دریافت می‌کنید، کافیست بر روی دکمه خرید گذاشته شده بزنید.

---

---

سوالات ریاضی تیزهوشان نهم ۹۸-۹۹

سوال ۷۱: اگر \(\Large A=\{1,\{1\},\{1,2\}\}  \) و \(\Large B=\{1,2\}  \) و \(\Large C=\{1,\{1\}\}  \) ، آنگاه کدام یک از گزینه‌های زیر نادرست است؟

1. \(\Large C \subseteq A  \)
2. \(\Large n(A \cap C)=2  \)
3. \(\Large A \cap B =\{1,2\}  \)
4. \(\Large (B-C) \cap A=\phi  \)

حل ۷۱: گزینه ۳

سوال ۷۲: مقدار عبارت \(\Large -(-5)^{-2}  \) با کدام یک از گزینه‌های زیر برابر است؟

1. \(\Large -(-5)^{2} \)
2. \(\Large -(-5^{-1})^{2}  \)
3. \(\Large -(-5^{2})^{-1}  \)
4. \(\Large -(-5^{-2})  \)

حل ۷۲: گزینه ۲

سوال ۷۳: چندتا از عددهای زیر به صورت نماد علمی نوشته شده است؟

• \(\Large \sqrt{7} \times 10^{-20} \)
• \(\Large 5/3 \times 2^{10} \)
• \(\Large (\frac{1}{3})^{-1} \times 10^{15} \)

1. صفر
2. ۱
3. ۲
4. ۳

حل ۷۳: گزینه ۳

سوال ۷۴: کدام یک از گزینه‌های زیر مجموعه جواب نامعادله زیر را نشان می‌دهد؟

\(\LARGE -3(x-1) \geq 1- \frac{2x+1}{2} \)

1. \(\Large \{x \in \mathbb{R}|x \leq \frac{5}{4}\} \)
2. \(\Large \{x \in \mathbb{R}|x \geq \frac{5}{4}\} \)
3. \(\Large\{x \in \mathbb{R}|x \leq \frac{3}{4}\} \)
4. \(\Large \{x \in \mathbb{R}|x \geq \frac{3}{4}\}  \)

حل ۷۴: گزینه ۱

سوال ۷۵: اگر \(\Large xyz \neq 0  \) و \(\Large m=\sqrt{-x^2y^3z^5}  \) یک عدد حقیقی باشد، آنگاه کدام یک از تساوی‌های زیر، همواره درست است؟

1. \(\Large m=-x\sqrt{y^3z^5} \)
2. \(\Large m=z\sqrt{-x^2y^3z^3} \)
3. \(\Large m=xy\sqrt{-yz^5} \)
4. \(\Large m=-yz\sqrt{-x^2yz^3}  \)

حل ۷۵: گزینه ۴

سوال ۷۶: اگر \(\Large A=a^2-b^2  \) و \(\Large B=a^2+b^2  \) و \(\Large C=ab \neq 0  \) حاصل عبارت \(\Large \frac{A^2-B^2}{C^2}  \) کدام گزینه است؟

1. ۴-
2. ۱
3. ۱-
4. ۴

حل ۷۶: گزینه ۱

سوال ۷۷: اگر \(\Large a  \) و \(\Large b  \) دو عدد گویا باشند به طوری که \(\Large |a| > |b|  \) و \(\Large (a+b) \in \mathbb{Z}  \) و \(\Large (a-b) \in (\mathbb{Q}-\mathbb{Z}) \) ،در این صورت چندتا از گزاره‌های زیر می‌تواند درست باشد؟

• \(\Large \frac{a}{b} \in \mathbb{Z} \)
• \(\Large \frac{a}{b} \in (\mathbb{Q}-\mathbb{Z}) \)
• \(\Large a=-2b \)

1. صفر
2. ۱
3. ۲
4. ۳

حل ۷۷: گزینه ۳

سوال ۷۸: کدام یک از عامل‌های زیر در تجزیه عبارت \(\Large (x^2-5x+6)+(x^2-x-2)  \) وجود دارد؟

1. \(\Large x-1  \)
2. \(\Large 2x+2  \)
3. \(\Large x+2 \)
4. \(\Large x-3  \)

حل ۷۸: گزینه ۱

---

---

سوال ۷۹: در یک آزمون ریاضی، ۳۰ سوال، طراحی شده است. هر پاسخ صحیح دارای ۴ امتیاز مثبت و هر پاسخ اشتباه دارای ۲ امتیاز منفی است و پرسش بدون پاسخ، امتیازی ندارد. نسیم در این آزمون، امتیاز ۴۶ را کسب کرده است. او حداکثر به چند پرسش پاسخ داده است؟

1. ۱۱
2. ۱۷
3. ۲۰
4. ۲۸

حل ۷۹: گزینه ۴

سوال ۸۰: اگر \(\Large D,C,B,A  \) چهار مجموعه باشند، به طوری که \(\Large ((A \cup B)-C)-D=D  \) آن‌گاه حاصل \(\Large A \cup B \cup C \cup D   \) همواره برابر است با:

1. \(\Large \phi  \)
2. \(\Large C  \)
3. \(\Large D  \)
4. \(\Large A \cup B  \)

حل ۸۰: گزینه ۲

سوال ۸۱: اگر حجم مکعب مقابل برابر ۴۳۲ واحد باشد، حجم هرم \(\Large ABCD   \) برابر کدام گزینه است؟

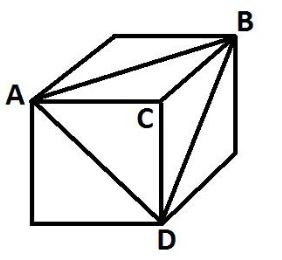
1. \(\Large 32\sqrt{3}  \)
2. \(\Large 32\sqrt [3] {2}   \)
3. \(\Large 72  \)
4. \(\Large 144  \)

حل ۸۱: گزینه ۳

سوال ۸۲: اگر در پرتاپ یک تاس بدانیم که عدد رو شده، شمارنده عدد ۶ نمی‌باشد، در این‌صورت تعداد کل پیشامدها برابر است با:

1. ۲
2. ۴
3. ۶
4. ۸

حل ۸۲: گزینه ۲

سوال ۸۳: اگر \(\Large 5x^3+A+1  \) بر \(\Large x^2+2x-1  \) بخش پذیر باشد و \(\Large A  \) یک چندجمله‌ای یک باشد، در این‌صورت \(\Large A  \) برابراست با:

1. \(\Large -15x+11  \)
2. \(\Large 15x-11  \)
3. \(\Large 25x-9  \)
4. \(\Large -25x+9  \)

حل ۸۳: گزینه ۴

سوال ۸۴: مثلث متساوی الاضلاع  \(\Large ABC  \) را همانند شکل روبه-رو نسبت به پاره‌خط \(\Large DE  \) تا زده‌ایم، مقدار \(\Large a  \) برابر با کدام گزینه است؟ \(\Large (\widehat{EDC}=52^o)  \)

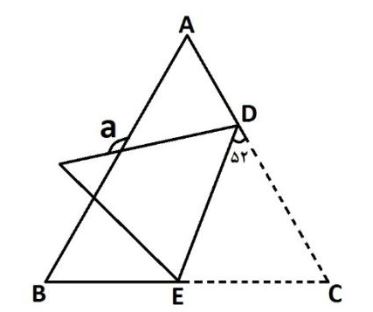
1. \(\Large 104^o  \)
2. \(\Large 106^o  \)
3. \(\Large 136^o  \)
4. \(\Large 156^o  \)

حل ۸۴: گزینه ۳

سوال ۸۵: متوازی الاضلاعی با اندازه اضلاع ۵ و ۹ سانتی متر و مساحت ۲۷ سانتی متر مربع را حول ضلع بزرگ آن دوران داده‌ایم. حجم شکل حاصل از دوران، برابر چند سانتی متر مکعب می‌باشد؟

1. \(\Large 27\pi  \)
2. \(\Large 81\pi  \)
3. \(\Large 225\pi  \)
4. \(\Large 243\pi  \)

حل ۸۵: گزینه ۲

سوال ۸۶: در مثلثی به ابعاد \(\Large \sqrt{41} , 8 , 5 \)، طول بلندترین ارتفاع مثلث، برابر کدام گزینه است؟

1. \(\Large 6/4 \)
2. \(\Large 4/8  \)
3. \(\Large 7/2  \)
4. \(\Large 5/4  \)

حل ۸۶: گزینه ۱

سوال ۸۷: اگر \(\Large x=\sqrt [3] {(-4)^{-2}} + \sqrt {2^{-4}} \) آن‌گاه حاصل \(\Large \frac {x}{1+ \sqrt [3] {4}} \) برابر است با:

1. \(\Large \frac {1+\sqrt [3] {2}}{4(1+\sqrt [3] {4})} \)
2. \(\Large \frac {1+2\sqrt [3] {4}}{4(1+\sqrt [3] {4})}  \)
3. \(\Large 1 \)
4. \(\Large \frac{1}{4} \)

حل ۸۷: گزینه ۴

سوال ۸۸: اگر دوجمله‌ای \(\Large \frac{2}{3}a^{(n+4m-6)}b^{(3n-5)}c^{(k-6)} \) و \(\Large \sqrt{6}a^{(2m+3n-3)}b^{(2m-3n)} \) متشابه باشند، حاصل \(\Large 3n+2m-2k \) برابر با کدام گزینه است؟

1. ۱
2. ۳
3. ۵
4. ۷

حل ۸۸: گزینه ۱

سوال ۸۹: چند خط متمایز، با معادله‌ی \(\Large ax+by=c \) که در شرایط زیر صدق کند، وجود دارد؟

• \(\Large a,b,c \) سه عدد صحیح و مخالف صفر هستند.
• عرض از مبدا خط، مثبت است.
• \(\Large |a|+|b|=3 \) و \(\Large ||ab|+c|=c-ab \) و \(\Large |c|=3 \)

1. صفر
2. ۲
3. ۴
4. بی‎‌شمار

حل ۸۹: گزینه ۲

سوال ۹۰: در شکل رو به رو \(\Large MA=MC=BC \) و \(\Large \widehat{BCM}=32^o  \) و \(\Large \widehat{MCA}=14^o  \) ، اندازه زاویه \(\Large \widehat{MAB}  \) چند درجه است؟

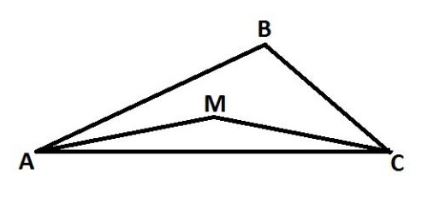
1. \(\Large 14^o  \)
2. \(\Large 28^o  \)
3. \(\Large 16^o  \)
4. \(\Large 32^o  \)

حل ۹۰: گزینه ۳

زنگ آخر پاسخنامه تشریحی سوالات ریاضی تیزهوشان نهم ۹۸-۹۹

دوستان ریاضیکا، حتما ویدیو و پاسخنامه تشریحی سوالات ریاضی تیزهوشان نهم ۹۸-۹۹ را تهیه کنید. هر سوالی داشتید در قسمت دیگاه می‌توانید از کارشناسان ریاضیکا بپرسید.

---

---