آموزش ریاضی پایه دوازدهم تجربی
مشتق پذیری دوازدهم تجربی 📸📝 – آموزش با مثال و تصویر
در آموزش مشتق پذیری دوازدهم تجربی میخواهیم بررسی کنیم در چه شرایطی یافتن مشتق تابع در یک نقطه امکانپذیر است. ابتدا شرط کلی مشتق پذیری را بیان میکنیم. سپس بررسی میکنیم در چه حالتهایی این شرط برقرار نیست.
شرط کلی مشتق پذیری
همانطور که پیش از این دیدیم، مشتق تابع \(\Large f(x) \) در نقطهٔ \(\Large a \)، به یکی از دو روش زیر محاسبه میشود:
- \(\LARGE f'(a)=\lim\limits_{h\to 0} \frac{f(a+h)-f(a)}{h}\)
- \(\LARGE f'(a)=\lim\limits_{x\to a} \frac{f(x)-f(a)}{x-a}\)
در صورتی که حاصل حدود بالا برابر با عدد حقیقی شود، میگوییم تابع در نقطهٔ \(\Large a \) مشتق پذیر است. لازم به ذکر است که فرض ما بر این است که نقطهی \(\Large a \) یکی از نقاط درونی دامنهی تابع است (در ادامهی درسنامه به نقاط ابتدایی و انتهایی نیز خواهیمپرداخت).
ممکن است برایتان سوال پیش بیاید که در چه شرایطی، حدود بالا موجود نیستند و تابع در یک نقطه مشتق پذیر نیست. در قسمت بعدی به بررسی این حالات میپردازیم.
حالات مختلف مشتق ناپذیری
در سه حالت، تابع در یک نقطه مشتق پذیر نیست:
- نامتناهی شدن حدود تعریف شده در مشتق
- ناپیوستگی
- نابرابری مشتق های چپ و راست
در ادامه به بررسی هر یک از این سه مورد میپردازیم.
نامتناهی شدن حدود تعریف شده در مشتق
همانطور که گفتیم، مشتق تابع \(\Large f(x) \) در نقطهٔ \(\Large a \) از رابطهٔ زیر به دست میآید:
\(\LARGE \lim\limits_{x\to a} \frac{f(x)-f(a)}{x-a}\)
اگر حاصل این حد نامتناهی شود، یعنی برابر با \(\Large +\infty \) یا \(\Large -\infty \) گردد، تابع در نقطهٔ \(\Large a \) مشتق پذیر نیست. دقت کنید، \(\Large +\infty \) و \(\Large -\infty \)، اعداد حقیقی نیستند. این دو نماد به همراه اعداد حقیقی، تشکیل مجموعهٔ دیگری میدهند که در این درس با آن کاری نداریم. (در صورتی که علاقهمندید، در مورد دستگاه اعداد حقیقی توسعه یافته تحقیق کنید). از این روست که در صورت نامتناهی شدن حد بالا، میگوییم تابع در نقطهی \(\Large a \) مشتق پذیر نیست.
مثال 1: تابع \(\Large f(x)=\sqrt[3]{x} \) که نمودار آن در شکل زیر رسم شدهاست، در چه نقطهای مشتق پذیر نیست؟
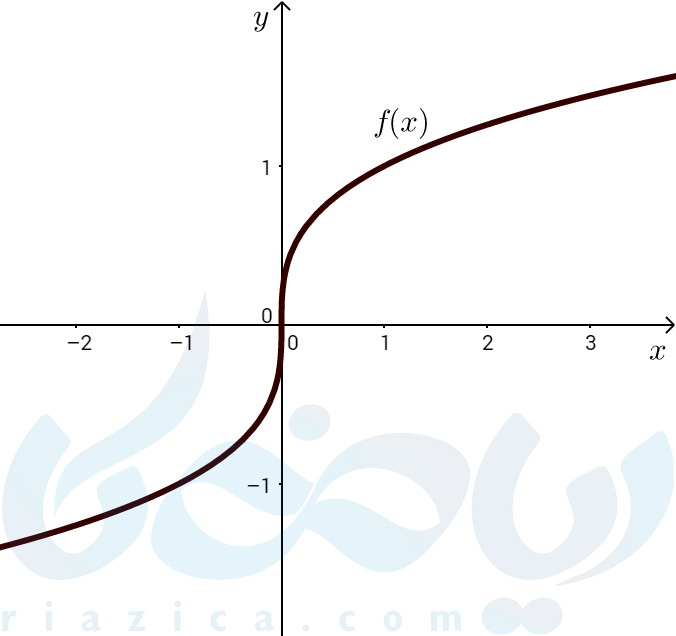
حل: اگر مشتق تابع در نقطهی \(\Large x=0 \) را محاسبه کنیم، خواهیمداشت:
\(\LARGE \lim\limits_{x\to 0} \frac{f(x)-f(0)}{x-0}\)
\(\LARGE =\lim\limits_{x\to 0} \frac{\sqrt[3]{x}-0}{x-0}\)
\(\LARGE =\lim\limits_{x\to 0} \frac{1}{\sqrt[3]{x^2}}\)
\(\LARGE =\infty\)
بنابراین، تابع \(\Large f(x) \) در نقطهی \(\Large x=0 \) مشتق پذیر نیست. در این حالت به خط \(\Large x=0 \) مماس قائم منحنی می گوییم.
ناپیوستگی
اگر ثابت کنیم مشتق پذیری تابع در یک نقطه، پیوستگی تابع در آن نقطه را نتیجه میهد، به صورت منطقی می توانیم نتیجه بگیریم که اگر تابع در یک نقطه ناپیوسته باشد، در آن نقطه مشتق پذیر نیست (در صورتی که علاقهمندید، می توانید در مورد عکس نقیض تحقیق کنید). در ادامه، قضیهای که گفتیم را ثابت میکنیم.
تابع \(\Large f(x) \) را در نقطهٔ \(\Large a \) مشتق پذیر میگوییم، هر گاه پاسخ حد زیر یک عدد حقیقی شود:
\(\LARGE \lim\limits_{x\to a} \frac{f(x)-f(a)}{x-a}\)
برای اینکه حد بالا یک عدد حقیقی شود، باید داشته باشیم:
\(\LARGE \lim\limits_{x\to a} f(x)=f(a)\)
در غیر این صورت، مخرج حد برابر با صفر شده و صورت آن غیر صفر خواهدبود. در نتیجه حاصل حد، نامتناهی میشود. همانطور که در قسمت قبل گفتیم، در صورتی که مقدار حد، نامتناهی شود، تابع در نقطهی \(\Large a \) مشتق پذیر نیست. پس حتما باید داشته باشیم:
\(\LARGE \lim\limits_{x\to a} f(x)=f(a)\)
و این همان شرط پیوستگی است که در سال یازدهم خواندید. در نتیجه، در صورتی که تابع در نقطهی \(\Large a \) مشتق پذیر باشد، در آن نقطه پیوسته است.
مثال 2: تابع \(\Large f(x)=\begin{cases}2x \quad x \neq 1 \\ 1 \quad \quad x=1 \\ \end{cases} \) که نمودار آن را در شکل زیر مشاهده میکنید، در چه نقطهای مشتق پذیر نیست؟
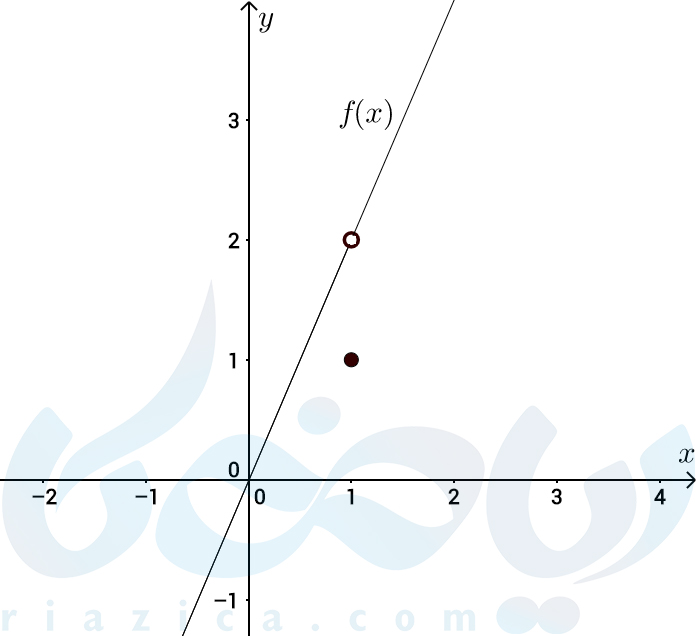
حل: همانطور که گفتیم، تابع در نقطهی ناپیوستگی مشتق پذیر نیست. در نقطهی \(\Large x=1 \) داریم:
\(\LARGE \lim\limits_{x\to 1} f(x)=2\)
\(\LARGE f(1)=1\)
در نتیجه \(\Large f(x) \) در \(\Large x=1 \) ناپیوسته است و مشتق پذیر نمیباشد.
برای اینکه درک بهتری داشته باشید، سعی میکنیم مشتق را در این نقطه محاسبه کنیم. خواهیمدید که در محاسبه شکست خواهیمخورد.
برای محاسبهی مشتق \(\Large f(x) \) در \(\Large x=1 \) داریم:
\(\LARGE \lim\limits_{x\to 1} \frac{f(x)-f(1)}{x-1}\)
\(\LARGE \lim\limits_{x\to 1} \frac{2x-1}{x-1}\)
\(\LARGE \lim\limits_{x\to 1} \frac{1}{x-1}\)
همانطور که میبینید، پاسخ حد بالا نامتناهی میشود. در نتیجه تابع در نقطهی \(\Large x=1 \) مشتق پذیر نیست. برای اینکه مشتق پذیری تابع \(\Large f(x) \) در یک نقطه را نیز دیده باشید، نقطۀ \(\Large x=2 \) را در نظر بگیرید. نشان میدهیم که مشتق \(\Large f(x) \) در این نقطه موجود بوده و بنابراین \(\Large f \) در \(\Large x=2 \) مشتق پذیر است. برای محاسبهٔ مشتق \(\Large f(x) \) در نقطهٔ \(\Large x=2 \) داریم:
\(\LARGE \lim\limits_{x\to 2} \frac{f(x)-f(2)}{x-2}\)
\(\LARGE \lim\limits_{x\to 2} \frac{2x-4}{x-2}\)
\(\LARGE \lim\limits_{x\to 2} \frac{2(x-2)}{x-2}=2\)
نابرابری مشتق های چپ و راست
ابتدا مشتق چپ و راست را تعریف میکنیم.
مشتق چپ تابع \(\Large f(x) \) در نقطهی \(\Large a \) با علامت \(\Large f’_-(a) \) نشان داده شده و برابر است با:
\(\LARGE f_{-}'(a)=\lim\limits_{h\to 0^-} \frac{f(a+h)-f(a)}{h}\)
یا به صورت معادل برابر است با:
\(\LARGE f_{-}'(a)=\lim\limits_{x\to a^-} \frac{f(x)-f(a)}{x-a}\)
مشتق راست تابع \(\Large f(x) \) در نقطهی \(\Large x=a \) با علامت \(\Large f’_+(a) \) نشان داده شده و برابر است با:
\(\LARGE f_{+}'(a)=\lim\limits_{h\to 0^+} \frac{f(a+h)-f(a)}{h}\)
یا به صورت معادل برابر است با:
\(\LARGE f_{+}'(a)=\lim\limits_{x\to a^+} \frac{f(x)-f(a)}{x-a}\)
برای وجود مشتق در یک نقطه، باید مشتقهای چپ و راست با هم برابر باشند. در غیر این صورت، حدودی که برای محاسبهی مشتق معرفی کردیم جواب نخواهندداشت. برای اینکه بهتر متوجه شوید، به مثال زیر دقت کنید.
مثال 3: تابع \( \Large f(x)= |x^2-4x+3| \) که نمودار آن در شکل زیر رسم شدهاست، در چه نقاطی مشتق پذیر نیست؟
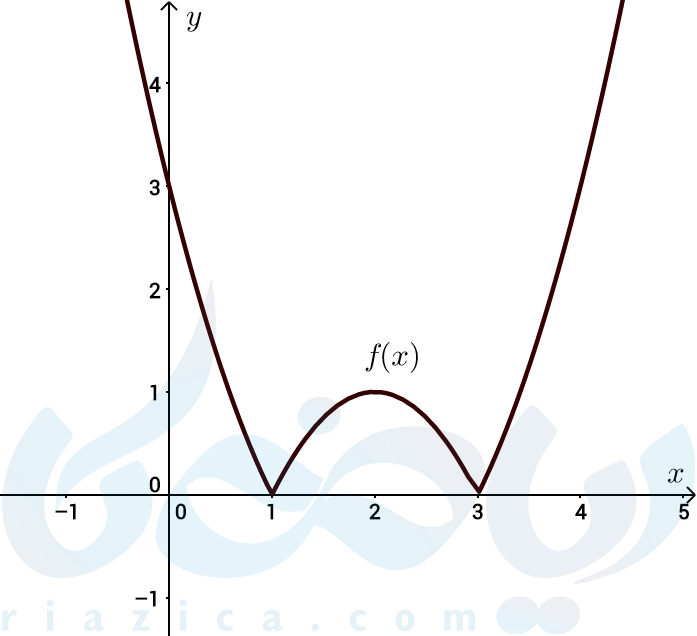
حل: از نمودار تابع میتوان حدس زد که مشتق چپ و راست در نقاط \(\Large x=1 \) و \(\Large x=3 \) برابر نیست.
در نقطهی \(\Large x=3 \)، مشتق چپ و راست به صورت زیر محاسبه میشوند:
\(\LARGE f_{-}'(3)=\lim\limits_{x\to 3^-} \frac{f(x)-f(3)}{x-3}\)
\(\LARGE =\lim\limits_{x\to 3^-} \frac{-x^2+4x-3-0}{x-3}\)
\(\LARGE =\lim\limits_{x\to 3^-} \frac{-(x-3)(x-1)}{x-3}\)
\(\LARGE =-2\)
میدانیم یک عبارت درجه دوم در بین دو ریشه مخالف علامت \(\LARGE a\)(ضریب \(\LARGE x^2\))است پس از درون قدر مطلق قرینه اش بیرون می آید ودر این مثال با مقادیر کمتر از ۳ به ۳ نزدیک میشویم پس این مقدار بین دو ریشه است.
\(\LARGE f_{+}'(3)=\lim\limits_{x\to 3^+} \frac{f(x)-f(3)}{x-3}\)
\(\LARGE =\lim\limits_{x\to 3^+} \frac{x^2-4x+3-0}{x-3}\)
\(\LARGE =\lim\limits_{x\to 3^+} \frac{(x-3)(x-1)}{x-3}\)
\(\LARGE =2\)
بنابراین مشتق چپ و راست در نقطهی \(\Large x=3 \) با یکدیگر برابر نیست.
به طور مشابه برای نقطهی \(\Large x=1 \) داریم:
\(\LARGE f’_-(1)=\lim\limits_{x\to 1^-} \frac{f(x)-f(1)}{x-1}\)
\(\LARGE =\lim\limits_{x\to 1^-} \frac{x^2-4x+3-0}{x-1}\)
\(\LARGE =\lim\limits_{x\to 1^-} \frac{(x-3)(x-1)}{x-1}\)
\(\LARGE =-2\)
\(\LARGE f’_+(1)=\lim\limits_{x\to 1^+} \frac{f(x)-f(1)}{x-1}\)
\(\LARGE =\lim\limits_{x\to 1^+} \frac{-x^2+4x-3-0}{x-1}\)
\(\LARGE =\lim\limits_{x\to 1^+} \frac{-(x-3)(x-1)}{x-1}\)
\(\LARGE =2\)
بنابراین در نقطهی \(\Large x=1 \) نیز مشتق چپ و راست با یکدیگر برابر نیست. بنابراین تابع در نقاط \(\Large x=1 \) و \(\Large x=3 \) مشتق پذیر نمیباشد.
مشتق پذیری روی یک بازه
تابع \(\Large f(x) \) را روی بازهٔ \(\Large (a, b) \) مشتق پذیر میگوییم، هرگاه در هر نقطه درون این بازه مشتق پذیر باشد.
اما اگر بخواهیم مشتق پذیری تابع را روی بازهٔ \(\Large [a, b] \) بررسی کنیم، باید برای نقاط \(\Large a \) و \(\Large b \) شروطی بگذاریم.
تابع \(\Large f(x) \) را روی بازهی \(\Large [a, b] \) مشتق پذیر میگوییم، هرگاه در بازهی \(\Large (a, b) \) مشتق پذیر بوده، در نقطهی \(\Large a \) مشتق راست و در نقطهی \(\Large b \) مشتق چپ داشته باشد.
مشتق پذیری روی بازههای \(\Large [a, b) \) و \(\Large (a, b] \) نیز به صورت مشابه تعریف میشود.
مثال از مشتق پذیری روی یک بازه
در مثال 1، تابع \(\Large f(x) \) در بازۀ \(\Large (1, +\infty) \) مشتق پذیر است. زیرا \(\Large f \) در هر نقطه درون این بازه مشتق پذیر است. دقت کنید که نقطۀ \(\Large x=1 \) درون بازۀ \(\Large (1, +\infty) \) قرار ندارد.
از طرفی تابع \(\Large f(x) \) در بازۀ \(\Large [1, +\infty) \) مشتق پذیر نیست. زیرا \(\Large f \) در نقطۀ \(\Large x=1 \) مشتق راست ندارد.
توصیه میشه در ادامه پست تابع مشتق را مطالعه کنید.
زنگ آخر کلاس مشتق پذیری دوازدهم تجربی
در این درسنامه به مبحث مشتق پذیری دوازدهم تجربی پرداختیم. همانطور که گفتیم، تابع در یک نقطه مشتق پذیر است اگر حد موجود در تعریف مشتق، پاسخ حقیقی داشته باشد. در سه حالت، تابع در یک نقطه مشتق پذیر نبود:
- نامتناهی شدن حدود تعریف شده در مشتق
- ناپیوستگی
- نابرابری مشتق های چپ و راست
هر یک از این سه مورد را با حل مثال بررسی کردیم. همچنین، در انتها تعریف مشتق پذیری تابع روی یک بازه نیز بررسی شد.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث مشتق پذیری دوازدهم تجربی دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.




