آموزش ریاضی پایه هشتم
بردارهای واحد مختصات 👣➡️ – قدم قدم بشمار!
ترتیبی که برای خواندن درسنامههای آموزش ریاضی هشتم به شما پیشنهاد میدهیم:
- زاویه های خارجی 🏰🔶 – نگهبان قلعه چندضلعیها!
- اعداد صحیح ↔️➖➕– نمایش روی محور مختصات
- زاویه های داخلی ❌⚔️ – نیروهای جوان کشور چندضلعیها!
- تعریف اعداد گویا و … ! ➗🔡 همه چیز اینجاست!
- عدد اول ریاضی هشتم 1️⃣👨🎓 – کاملترین آموزشی که لازم داشتید.
- اعداد گویا – ✖️➗➖➕ چهار عمل اصلی
- رابطه فیثاغورس ریاضی هشتم 🎮📐 – وزیر بازی مثلثات!
- خط تقارن ریاضی هشتم ✂️ – چندضلعی تا خورده!
- خط و دایره : از سیر ➖ تا پیاز 🔴
- خطوط موازی و مورب #️⃣🚘 ؛ رانندگی خطها در چهارراه زاویه!
- چهار ضلعی ها ✏️🔶 – آشنایی با یک خانواده جذاب!
- ساده کردن عبارت های جبری 📣🎓 ؛ مختصر و مفید با صدای بلند!
- فاکتورگیری ریاضی هشتم 🔡➕➖ – هنرمندانه از عبارتهای جبری استفاده کن!
- حل معادله درجه اول 🍩📝 – سرآغاز یک بحث شیرین ریاضی!
- بردار و مختصات ریاضی هشتم ➡️⬅️ – جهتدار و کامل!
- بردارهای واحد مختصات 👣➡️ – قدم قدم بشمار!
- شکل های هم نهشت آموزش ریاضی هشتم 🔷🔶 – کپی برابر اصل!
- مثلث های هم نهشت 🌷🔺 گل سرسبد شکلهای همنهشت!
- با ضرب و تقسیم اعداد توان دار ➗✖️، توانت رو بالا ببر! آموزش ریاضی هشتم
- جذر تقریبی هشتم 👣✅ – گام به گام یاد بگیر
- نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم ✏️🔛 یک نمایش بی نقص
- خواص ضرب و تقسیم رادیکال ها ریاضی هشتم ✖️➗ – یکضرب یاد بگیر!
- همه چیز درباره جدول فراوانی 📊📝 ریاضی هشتم – دادههای آماری
- آموزش احتمال هشتم 💰🎲 : احتمال رخ دادن پیشامد – احتمالاً نه! حتماً یاد میگیرید
- زاویه های دایره : زاویه محاطی و زاویه مرکزی ⭕️📍 – مبحثی کاربردی در هندسه!
- جمع و تفریق اعداد صحیح ➕➖ – صحیح و سالم به مقصد برسید!
یاد قدیما بخیر؛ قبل از ساختن ساختمون میرفتن سر زمین، با قدم زمین رو متر میکردن – یه قدم راست، یه قدم بالا! بردارهای واحد مختصات دقیقاً همون کار رو انجام میدن، ولی این بار روی کاغذ و در درس ریاضیات! در این محتوا از مجموعه آموزش ریاضی پایه هشتم، خواهیم دید که برای شمارش و اندازهگیری هر چیزی نیاز به واحد داریم و برای بردارها هم واحد وجود دارد. با استفاده از بردارهای واحد، به رسم بردار و حل معادله مختصاتی خواهیم پرداخت.
مقدمهای قبل از « بردارهای واحد مختصات »
هر کمّیت (چیزی که قابل شمارش یا اندازهگیری باشد) دارای یک واحد اندازهگیری است که به کمک این واحد میتوانیم ابعاد بزرگ و کوچک را شمارش کنیم. (این واحد، شبیه همان قدم در متر کردن زمین ساختمان است!)
اگر در یک اتاق تنها تکه چوبی داشته باشید و به شما گفتهاند که اندازه آن 15 سانتیمتر است، از آن به عنوان واحد اندازهگیری استفاده میکنید. مثلاً اگر طول نردبان 8 برابر این تکه چوب باشد، طول آن میشود:
\( \Large 8 × 15 = 120 \)
تعریف واحد اندازهگیری
مقداری ثابت و معیّن از یک کمیّت که بصورت قراردادی به عنوان معیاری برای اندازهگیری و شمارش آن کمیّت انتخاب میشود. به عنوان نمونه، واحد اندازهگیری چند کمیّت در جدول زیر نشان داده شده است:
| کمیت | واحد اندازهگیری |
|---|---|
| طول | متر |
| جرم | کیلوگرم |
| دما | درجه سانتیگراد |
| زاویه | درجه |
| زمان | ثانیه |
مثال 1: برای محور اعداد نیز واحد وجود دارد که در شکل زیر نمایش داده شده است. با توجه به این واحد، اعداد 3 و 2- را نشان دهید.

حل 1:
فاصله بین 0 تا 1 به عنوان واحد نشان داده شده است؛ پس برای نمایش عدد 3، باید سه برابر این واحد به سمت مثبت (راست محور) و برای نمایش عدد (2-)، دو برابر مقدار واحد به سمت منفی (چپ محور) از مبدأ مختصات (0) حرکت کنیم:

بردارهای واحد مختصات
مانند واحدهای نشان داده شده در بالا، برای نمایش بردار نیز به واحد نیاز داریم و این واحد باید از جنس بردار باشد. میدانیم بردار در صفحه مختصات با 2 محور نمایش داده میشود؛ پس 2 بردار واحد مختصات داریم:
(بردار واحد طول) \( \Large {\rm{\;}}\vec i = {\rm{ }}\left[ {\begin{array}{*{20}{l}}{\rm{1}}\\{\rm{0}}\end{array}} \right] \)
(بردار واحد عرض) \( \Large \vec j = \left[ {\begin{array}{*{20}{l}}{\rm{0}}\\{\rm{1}}\end{array}} \right] \)
این بردارها در صفحه مختصات زیر نشان داده شدهاند؛ همانطور که میبینید بردار واحد طول به اندازه یک واحد از مبدأ به سمت راست و بردار واحد عرض به اندازه یک واحد از مبدأ به سمت بالا رسم میشود.
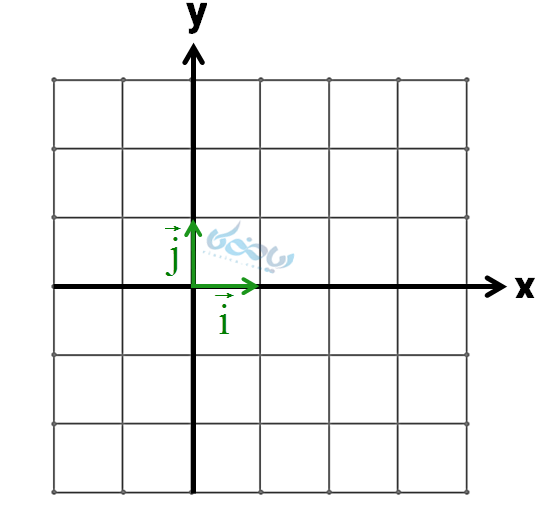
مثال 2: بردار \( \Large \overrightarrow {a} = -2 \overrightarrow {i} + 3 \overrightarrow {j} \) را رسم کنید و مختصات این بردار را بنویسید.
حل 2:
از درسنامه بردار و مختصات ریاضی هشتم، روش جمع بردارها و رسم بردار برآیند و همچنین نحوه ضرب عدد در بردار را یاد گرفتیم؛ میتوانیم \( \Large \overrightarrow {i} \) و \( \Large \overrightarrow {j} \) را دو بردار در نظر گرفته و از روش گفته شده استفاده کنیم.
اما بردارهای واحد مختصات کار را سادهتر کردهاند! کافی است از مبدأ مختصات شروع کرده، 2 واحد به سمت چپ (منفی) و سه واحد به سمت بالا (مثبت) حرکت کنیم:
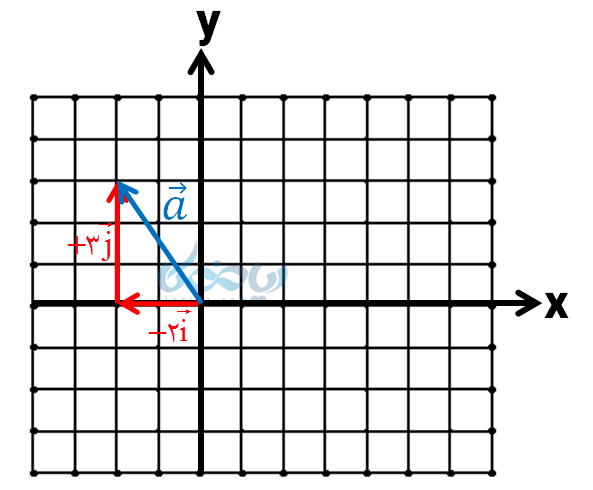
مختصات بردار \( \Large \overrightarrow {a} \) همانگونه که در شکل مشاهده میشود برابر است با:
\( \LARGE \vec a = \left[ {\begin{array}{*{20}{l}}{{\rm{ – 2}}}\\{\rm{3}}\end{array}} \right] \)
نوشتن بردار بر حسب بردارهای واحد مختصات
برای تبدیل یک بردار به بردارهای واحد مختصات، کافی است عدد طول مختصات را به عنوان ضریب \( \Large \overrightarrow {i} \) و عدد عرض مختصات را به عنوان ضریب \( \Large \overrightarrow {j} \) در نظر بگیریم:
\( \Large \overrightarrow {\rm{a}} = \left[ \begin{array}{l}{\rm{m}}\\{\rm{n}}\end{array} \right] \)
\( \Large \overrightarrow {\rm{a}} = {\rm{ m }}\overrightarrow {\rm{i}} {\rm{ + n }}\overrightarrow {\rm{j}} \)
مثال 3: بردار \( \Large \overrightarrow {\rm{V}} = \left[ \begin{array}{l}{\rm{4}}\\{\rm{ – 2}}\end{array} \right] \) را بر حسب بردارهای واحد مختصات بنویسید.
حل 3:
همانطور که میبینیم طول و عرض مختصات بردار \( \Large \overrightarrow {V} \) به ترتیب برابر با (4) و (2-) هستند؛ پس این اعداد را به ترتیب به عنوان ضرایب \( \Large \overrightarrow {i} \) و \( \Large \overrightarrow {j} \) در نظر میگیریم و با جمع آنها خواهیم داشت:
\( \Large \overrightarrow {\rm{V}} = {\rm{ 4 }}\overrightarrow {\rm{i}} {\rm{ + ( – 2) }}\overrightarrow {\rm{j}} \)
\( \Large \overrightarrow {\rm{V}} = {\rm{ 4 }}\overrightarrow {\rm{i}} {\rm{ }} – {\rm{2 }}\overrightarrow {\rm{j}} \)
مثالی از جمع برداری با بردارهای واحد مختصات
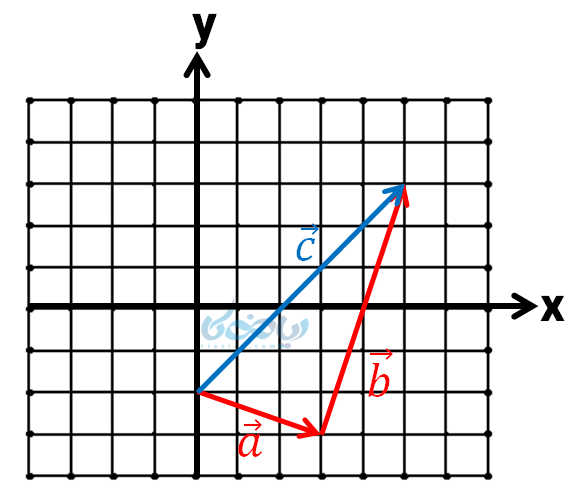
مثال 4: جمع برداری نشان داده شده در شکل را بر حسب بردارهای واحد مختصات نوشته و بردار برایند را بدست آورید.
حل 4:
مشاهده میکنیم که بردارهای \( \Large \overrightarrow {a} \) و \( \Large \overrightarrow {b} \) با هم جمع شده و بردار برایند \( \Large \overrightarrow {c} \) را ایجاد کردهاند.
بردار \( \Large \overrightarrow {a} \)، 3 واحد به سمت راست و 1 واحد به سمت پایین کشیده شده است؛ پس مختصات آن بدین صورت خواهد بود:
\( \Large \overrightarrow {\rm{a}} = {\rm{ 3 }}\overrightarrow {\rm{i}} {\rm{ }} – {\rm{ }}\overrightarrow {\rm{j}} \)
همچنین بردار \( \Large \overrightarrow {b} \)، 2 واحد به سمت راست و 6 واحد به سمت بالا کشیده شده است؛ پس مختصات آن بدین صورت خواهد بود:
\( \Large \overrightarrow {\rm{b}} = {\rm{ 2 }}\overrightarrow {\rm{i}} {\rm{ }} + {\rm{6 }}\overrightarrow {\rm{j}} \)
حال میتوان جمع برداری را برای این شکل با استفاده از بردارهای واحد مختصات نوشت:
\( \Large \overrightarrow {\rm{c}} = {\rm{ }}\overrightarrow {\rm{a}} {\rm{ }} + \overrightarrow {\rm{b}} \)
\( \Large \overrightarrow {\rm{c}} = {\rm{ (3 }}\overrightarrow {\rm{i}} {\rm{ }} – {\rm{ }}\overrightarrow {\rm{j}} {\rm{) + (2 }}\overrightarrow {\rm{i}} {\rm{ }} + {\rm{6}}\overrightarrow {\rm{j}} {\rm{)}} \)
حال برای جمع این دو بردار، ضرایب \( \Large \overrightarrow {i} \) را در کنار هم و ضرایب \( \Large \overrightarrow {j} \) را نیز در کنار هم مینویسیم:
\( \Large \overrightarrow {\rm{c}} = {\rm{ (3 + 2) }}\overrightarrow {\rm{i}} {\rm{ + (( – 1)}} + {\rm{6)}}\overrightarrow {\rm{j}} \)
\( \LARGE \overrightarrow {\rm{c}} = {\rm{ 5 }}\overrightarrow {\rm{i}} {\rm{ + 5}}\overrightarrow {\rm{j}} \)
معادلات مختصاتی
معادلات مختصاتی را دقیقاً مانند معادلات معمولی حل میکنیم؛ پس برای حل آنها باید مراحل زیر را طی کنیم:
- مجهولات را به یک طرف تساوی و مختصات را به طرف دیگر منتقل میکنیم؛
- مجموع مجهولات و مجموع مختصات را به دست میآوریم؛
- مختصات را بر ضریب مجهول تقسیم میکنیم.
تذکر: اگر مختصات یا مجهولات از یک طرف به طرف دیگر تساوی منتقل شود، علامت آن عوض میشود.
مثال 5: معادلات مختصاتی زیر را حل کنید.
الف) \( \Large \left[ \begin{array}{l}{\rm{ – 3}}\\{\rm{2}}\end{array} \right]{\rm{ – 2}}\overrightarrow {\rm{x}} = \left[ \begin{array}{l}{\rm{5}}\\{\rm{6}}\end{array} \right] \)
الف)
مرحله اول: انتقال مجهول به یک طرف و مختصات به طرف دیگر
\( \Large \left[ \begin{array}{l}{\rm{ – 3}}\\{\rm{2}}\end{array} \right]{\rm{ – }}\left[ \begin{array}{l}{\rm{5}}\\{\rm{6}}\end{array} \right] = {\rm{2}}\overrightarrow {\rm{x}} \)
مرحله دوم: محاسبه حاصلجمع مجهولات و حاصل جمع مختصات
\( \Large \left[ \begin{array}{l}{\rm{ – 8}}\\{\rm{ – 4}}\end{array} \right] = {\rm{2}}\overrightarrow {\rm{x}} \)
مرحله سوم: تقسیم مختصات به ضریب مجهول
\( \Large \overrightarrow {\rm{x}} = \frac{{\rm{1}}}{{\rm{2}}}\left[ \begin{array}{l}{\rm{ – 8}}\\{\rm{ – 4}}\end{array} \right] = \left[ \begin{array}{l}{\rm{ – 4}}\\{\rm{ – 2}}\end{array} \right] \)
نمونهای ترکیبی از بردارهای واحد مختصات و معادلات مختصاتی
ب) \( \Large \overrightarrow {\rm{a}} + {\rm{3 }}\overrightarrow {\rm{i}} = {\rm{2}}\overrightarrow {\rm{a}} – {\rm{3}}\left[ \begin{array}{l}{\rm{1}}\\{\rm{ – 2}}\end{array} \right] \)
ب) در این مثال، هم بردارهای واحد مختصات و هم بردارهای معمولی وجود دارد؛ در اینگونه موارد برای این که بتوانیم جمع یا تفریق کنیم، یا بردارهای واحد را به بردارهای معمولی تبدیل میکنیم یا بالعکس. مانند مثال (الف) در اینجا هم مرحله به مرحله پیش میرویم:
مرحله اول: انتقال مجهول به یک طرف و مختصات به طرف دیگر
\( \Large {\rm{3 }}\overrightarrow {\rm{i}} + {\rm{3}}\left[ \begin{array}{l}{\rm{1}}\\{\rm{ – 2}}\end{array} \right] = {\rm{2}}\overrightarrow {\rm{a}} – \overrightarrow {\rm{a}} \)
مرحله دوم: محاسبه حاصلجمع مجهولات و حاصل جمع مختصات (در این مرحله بردار واحد مختصات را بصورت بردار نوشتهایم)
\( \Large {\rm{3}}\left[ \begin{array}{l}{\rm{1}}\\{\rm{0}}\end{array} \right] + {\rm{3}}\left[ \begin{array}{l}{\rm{1}}\\{\rm{ – 2}}\end{array} \right] = \overrightarrow {\rm{a}} \)
\( \Large \left[ \begin{array}{l}{\rm{3}}\\{\rm{0}}\end{array} \right] + \left[ \begin{array}{l}{\rm{3}}\\{\rm{ – 6}}\end{array} \right] = \overrightarrow {\rm{a}} \)
\( \Large \overrightarrow {\rm{a}} = \left[ \begin{array}{l}{\rm{3 + 3}}\\{\rm{0 + ( – 6)}}\end{array} \right] = \left[ \begin{array}{l}{\rm{6}}\\{\rm{ – 6}}\end{array} \right] \)
مرحله سوم: تقسیم مختصات به ضریب مجهول (ضریب بردار \( \Large \overrightarrow {a} \) برابر است با 1)
\( \LARGE \overrightarrow {\rm{a}} = \left[ \begin{array}{l}{\rm{6}}\\{\rm{ – 6}}\end{array} \right] \)
زنگ آخر کلاس بردارهای واحد مختصات
این درس را با کلیاتی از واحدهای اندازهگیری و تعریف آن با مثالهای ساده ولی کاربردی آغاز کردیم و در ادامه با بردارهای واحد مختصات آشنا شدیم و دیدیم میتوانیم هر برداری را با توجه به جهت حرکت افقی و قائم بر حسب این بردارها بنویسیم. در انتها معادلههای مختصاتی را فرا گرفتیم و با حل مثال و ترکیب آن با بردارهای واحد این درس را کاملاً یاد گرفتیم.
در صورتی که هر سؤالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاهها برایمان بنویسید. کارشناسان ریاضیکا به سؤالات شما پاسخ خواهند داد.





سلام .
بردار های واحد مختصات باهم برابرند
با سلام وعرض ادب
بردار واحد طول به اندازه یک واحد از مبدأ به سمت راست و بردار واحد عرض به اندازه یک واحد از مبدأ به سمت بالا رسم میشود. پس از نظر اندازه برابرند ولی در دو راستای مختلف هستند
سلام ببخشید یک سوالی داشتم.میخواستم بدونم که بردارهای واحد رو فقط با i و j نشون میدن؟ مثلا من دیدم که با α و β هم نشون میدن.
ضمن عرض سلام
تا جایی که ما تجربه داریم بیشتر با i و j نشان میدهند.
در بردار AB نقطه ی ابتدا ………است
لطفا زود جواب بدین
نقطه A
سلام
منظورتون رو از متر کردن زمین با قدم متوجه نشدم، اینجایی که گفتین یک قدم راست، یک قدم بالا
با سلام
در زمانهای قدیم که وسایل اندازه گیرینبود از قدم یا وجب برای اندازه گیری استفاده میشد
اگر ……. بردار مساوی صفر باشد آنگاه بردار موازی طول ها است
لطفا جواب بدید
با سلام
عرض بردار صفر باشد