آموزش ریاضی پایه نهم
استدلال ریاضی نهم – ⚜️🔢 منطق ریاضی استفاده کن!
در مبحث استدلال ریاضی نهم میخواهیم به سوالهای زیر پاسخ دهیم:
- استدلال چیست؟
- مثال نقض چیست و کجا استفاده میشود؟
- آیا از ترسیم، شهود و یا حواس میتوان به عنوان استدلال حل مسئله استفاده کرد؟
پاسخ این سوالات را به همراه حل مثالهای جالب، در ادامۀ درسنامه استدلال ریاضی نهم خواهید یافت.
منظور از استدلال چیست؟
طبق تعریف کتاب ریاضی نهم، “استدلال یعنی دلیل آوردن و استفاده از دانستههای قبلی، برای معلوم کردن موضوعی که در ابتدا مجهول بوده است”. به زبان خیلی ساده، استدلال همان دلایل و روشهایی است که برای حل یک مسئله استفاده میکنیم. برای اینکه بهتر متوجه شوید، به مثال زیر از درس استدلال ریاضی نهم توجه کنید.
مثال از استدلال
مثال 1: دو استخر \(\Large A\) و \(\Large B\) داریم. استخر \(\Large A\) دارای طول 30 متر، عرض 15 متر و عمق 3 متر است. استخر \(\Large B\) دارای طول 25 متر، عرض 20 متر و عمق 4 متر است. کدام استخر ظرفیت بیشتری برای گنجایش آب دارد؟
حل: حجم یک مکعب مستطیل برابر است با حاصل ضرب طول، عرض و ارتفاع آن. اگر حجم آبی که در استخر \(\Large A\) گنجانده میشود را با \(\Large V_A\) و حجم آبی که در استخر \(\Large B\) گنجانده میشود را با \(\Large V_B\) نشان دهیم، داریم:
\(\Large V_A=30 \times 15 \times 3=1350\)
\(\Large V_B=25\times 20\times 4=2000\)
بنابراین ظرفیت گنجایش استخر \(\Large B\) بیشتر است. هماطور که دیدید، با استفاده از رابطهای که برای محاسبۀ حجم مکعب مستطیل داشتیم و محاسبۀ حجم آب هر استخر، استدلال کردیم که ظرفیت استخر \(\Large B\) بیشتر است. این یک استدلال درست بر پایۀ گزارههایی بود که درستی آنها را از قبل میانستیم. اما استدلال غلط نیز وجود دارد. به قسمت بعد از درسنامۀ استدلال ریاضی نهم توجه کنید.
استدلال غلط
ممکن است استدلال ما با توجه به منطق ریاضی غلط باشد. استدلال غلط ممکن است به نتیجۀ درست یا نتیجۀ غلط منجر شود. مثلاً فرض کنید در پاسخ به مثال قبل میگفتیم چون حرف \(\Large B\) در حروف الفبای انگلیسی بعد از \(\Large A\) قرار دارد، در نتیجه استخر \(\Large B\) دارای ظرفیت بیشتری است. استدلال ما کاملاً غلط بود اما به نتیجۀ درست منجر میشد. در هر صورت، نتیجه هر چه باشد، اگر استدلال از نظر منطق ریاضی نامعتبر باشد، فاقد ارزش است.
مثال نقض
زمانی که برای نشان دادن نادرستی یک نتیجه گیری کلی، مثالی میزنیم که نامعتبر بودن نتیجه گیری را در حالت کلی نشان میدهد، اصطلاحاً از مثال نقض استفاده کردهایم. برای اینکه بهتر متوجه شوید، به مثال بعدی از مبحث استدلال ریاضی نهم توجه کنید.
مثال 2: ثابت کنید حکم”ارتفاعهای هر مثلث، درون مثلث یکدیگر را قطع میکنند” نادرست است.
حل: کافی است مثلث زیر را در نظر بگیریم:
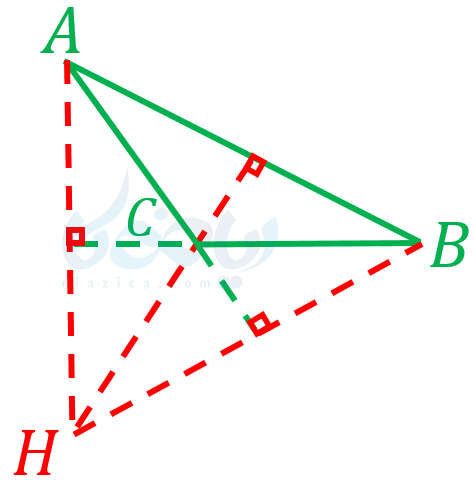
همانطور که میبینید در مثلث شکل بالا، ارتفاعهای مثلث، خارج از مثلث، در نقطۀ \(\Large H\) یکدیگر را قطع کردهاند. مثلث \(\Large ABC\) در شکل بالا، مثالی است که حکم”ارتفاعهای هر مثلث، درون مثلث یکدیگر را قطع میکنند” را نقض میکند. بنابراین مثلث \(\Large ABC\) مثال نقضی است برای حکم داده شده در مسئله. مثلثهای زیادی هستند که ارتفاعهایشان درون مثلث یکدیگر را قطع میکنند؛ اما، نمیتوان این حکم را به صورت کلی برای همۀ مثلثها در نظر گرفت. به قسمت بعد از درسنامۀ استدلال ریاضی نهم توجه کنید.
ترسیم، شهود و حواس و اندازهگیری
برای حل مسائل مختف ریاضی، از ترسیم شکل، شهود و احساس میتوان کمک گرفت؛ اما آیا از آنها به عنوان استدلال نیز میتوان استفاده کرد؟ پاسخ منفی است. به طور مثال فرض کنید در مسئلهای، چهارضلعی زیر داده شده است:
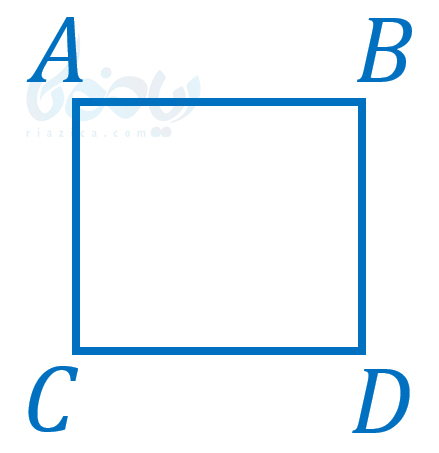
با اینکه حس ما میگوید چهارضلعی \(\Large ABCD\) در شکل بالا مربع است، اما به هیچ عنوان نمیتوانیم به این موضوع استدلال کنیم. تا زمانی که در صورت مسئله ذکر نشده که چهارضلعی \(\Large ABCD\) مربع است، مجاز نیستیم فرض کنیم \(\Large ABCD\) مربع است. تنها زمانی میتوانیم فرض کنیم \(\Large ABCD\) مربع است که در صورت مسئله ذکر شده باشد.
در تجربه، نگاه و احساس همیشه امکان خطا وجود دارد. شهود و احساس می توانند در یافتن پاسخ یک مسئله به ما کمک کنند اما نمی توانند به عنوان استدلال حل مسئله مورد استقاده قرار گیرند. حتی از اندازه گیری که نسبت به موارد قبل دارای دقت بیشتری است، نمیتوان به عنوان استدلال حل مسئله استفاده کرد. همیشه در اندازهگیری خطا وجود دارد. ممکن است میزان این خطا بسته به امکانات اندازه گیری، کم یا زیاد شود اما هیچ وقت صفر نمیشود. هم وسایل اندازه گیری دارای خطا هستند و هم انسان به عنوان کاربری که اندازهگیری را انجام میدهد دارای خطاست. مثالهای متنوع از خطای دید، ما را متقاعد میکنند که نگاه و تجربه، آنچنان هم که فکر میکنیم قابل اعتماد نیستند. به مثالهای بعدی از مبحث استدلال ریاضی نهم دقت کنید.
مثال از خطای دید
مثال1: به طور مثال شکل زیر که به خطای دید زولنر مشهور است را در نظر بگیرید:

احساس ما میگوید که خط های مورب شکل بالا با یکدیگر موازی نیستند. اما اینطور نیست! این تنها خطای چشم ماست. بنابراین همانطور که تایید کردیم، احساس، نگاه و شهود برای حل مسائل قابل اعتماد نیستند. اگرچه گاهی میتوانند برای یافتن راه حل درست به ما کمک کنند.
مثال 2: به شکل زیر که به خطای دید پونزو معروف است نگاه کنید.
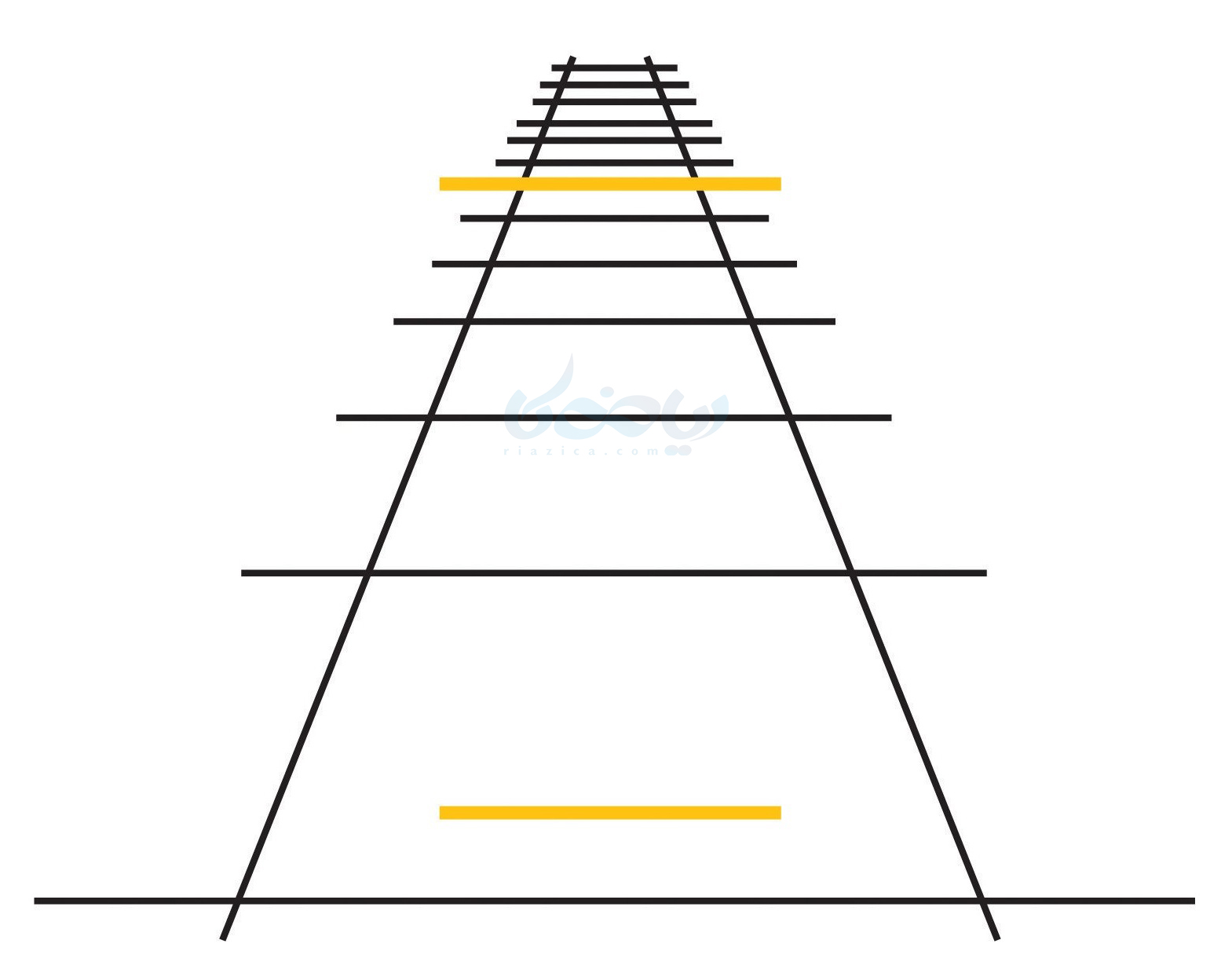
به نظر میآید طول پاره خط زردرنگ بالایی بیشتر است. در حالی که این طور نیست. هر دو پارهخط زردرنگ دارای طول یکسان هستند. مثال بعدی از این دو مثالی که دیدید هم عجیبتر است. به مثال بعدی از درسنامۀ استدلال ریاضی نهم دقت کنید.
مثال 3: به شکل زیر نگاه کنید. به نظر میرسد که خانۀ A از خانۀ B تاریکتر است.

اما اینطور نیست. هر دو خانه دارای یک رنگ هستند. اگر مانند شکل زیر یک مستطیل هم رنگ با این دو خانه، بین آنها رسم کنیم، بهتر متوجه میشویم که تصور ما غلط بوده است.
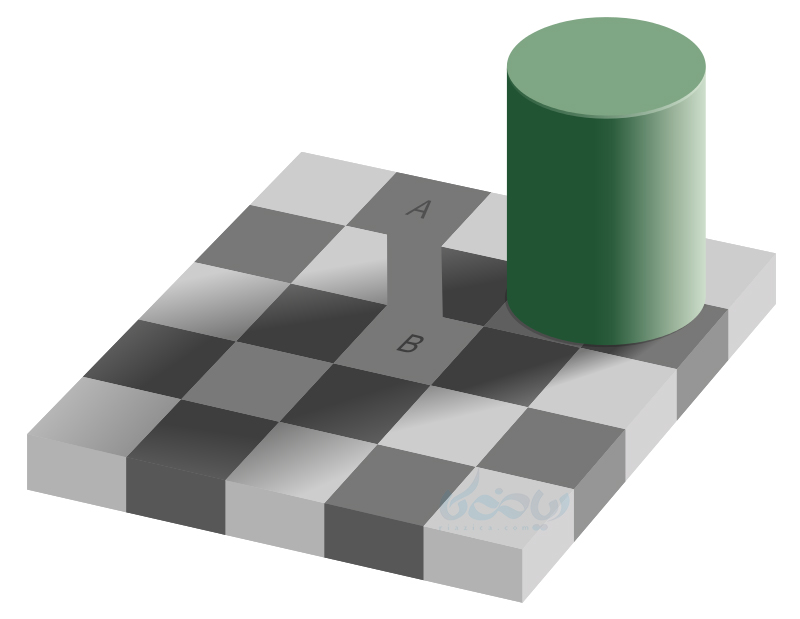
زنگ آخر کلاس استدلال ریاضی نهم
با استدلال در ریاضی نهم به صورت خیلی مقدماتی آشنا شدیم. دیدیم که برای نشان دادن نادرستی حکمهایی که برای حالتهای کلی مطرح میشوند، یک مثال نقض کافی است. همچنین دیدیم که با وجود مفید بودن شهود و احساس در کمک به یافتن راه حل یک مسئله، نمیتوان از آنها به عنوان استدلال استفاده کرد. در شهود و احساس احتمال وجود خطا هست. بنابراین استدلال ما باید تنها بر پایۀ منطق ریاضی باشد.ما در سالهای بعد با روشهای مختلف استدلال قضایا آشنا بیشتر می شویم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث استدلال ریاضی نهم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





خیلی خیلی خیلی خوب است
سلام و عرض ادب
ممنون از پیام دلنشینتون و انرژی بی دریغتون که به ما دادید.
موفق باشید.
چطور باید یه مسئله رو اثبات کنیم؟!
با سلام وعرض ادب هر مسئله راه حل خودش رو داره ولی https://riazica.com/problem-solving-in-geometry/ این وhttps://riazica.com/proofs-in-geometry/این پست به شما کمک میکنه بهتر متوجه بشید
چه استدلالی معتبر است؟
با سلام و عرض ادب
استدلال استنتاجی که بر اساس اصول و تعاریف و حقایق ریاضی که درستی آن از قبل برای ما محرز شده یک نوع استدلال معتبر در ریاضی است.
خیلی خوب
سلام و عرض ادب
ممنون از شما دوست عزیز
سلام و عرض ادب
ممنون از شما دوست عزیز
با عرض سلام ممنون از توضیحات عالیتون ولی من هر کاری میکنم نمیتونم بیشتر سوالات مربوط به این درس را حل کنم شما چه پیشنهادی میدهید هر تدریسی هم نگاه میننم نمیتوانم حل کنم لط۴ا بهم کمک کنید
با سلام وادب
فقط با حل مسئله زیاد از این قسمت میتونید مهارت حل مسئله خودتون رو بالا ببرید راه دیگهای نیست وفوری سراغ جواب نرید خودتون رو با مسئله به مدت طولانی درگیر کنید وراه حلهای مختلف روامتحان کمید
آیا در همه مسائل باید همیشه استدلال را مشخص کرد ید بانوشتن فرض و حکم کافی است؟؟؟؟؟
با سلام
استدلال حتما باید نوشته شود واصل حل یک مسئله است
با سلام و خسته نباشید خدمت شما دوست عزیز
من توی ریاضی بینهایت مشکل دارم و یک تنفر بسیار زیادی نسبت به ریاضی دارم جوری که فردا امتحان دارم اونم حضوری ولی نمیتونم یه سوال رو حل کنم. بحث فهمیدنش هم هست من تمرین هم میکنم ولی نمیفهمم! این سه سال رو من از ریاضی هیچی نفهمیدم و واقعا نمیدونم باید چیکار کنم
فکر میکنید من چیکار میتونم بکنم تا ریاضیم بهتر شه که حداقل امسال رو نیوفتم؟
با سلام وادب
اولا دیدگاهتون رو نسبت به ریاضی عوض کنید وباور کنید میشه یادش گرفت وباهاش دوست باشید ودر صلح دربیایید
ثانیا برای جبران عقب افتادگیتون مجبورید معلم خصوصی بگیرید تا خودتون رو به سطح کلاس برسونید
خیلی خیلی خوب بود
با سلام وادب
ممنون دوست عزیز
سلام من هم با دیدگاهتون موافقم ریاضی درس خوب وشیرین است ورشنگر معز انسان باید زحمت کشید وتمرین کرد
با سلام وادب
ممنون دوست عزیز
سلام موافقم
سلام مرسییییییییی عالیییی بودش❤️❤️❤️
با سلام ممنون از نگاه وانرژی شما به ما