آموزش ریاضی پایه نهم
اتحاد ریاضی نهم 3️⃣💢 – ۳ اتحاد مشهور!
در درسنامۀ اتحاد ریاضی نهم ابتدا اتحاد جبری را معرفی میکنیم. پس از آشنا شدن با مفهوم اتحاد، سه اتحاد مربع دو جمله ای، مزدوج و جمله مشترک را بررسی کرده و با حل مثال، کاربرد آنها را در ساده سازی عبارات جبری و محسابات ریاضی خواهیم دید. با ما تا انتهای درسنامه همراه باشید.
اتحاد جبری
اگر دو عبارت جبری داشته باشیم به طوری که مقدار دو عبارت با هر مقدار دهی یکسان به متغیرهایشان با هم برابر شوند، دو عبارت جبری با یکدیگر متحد هستند. به برابری آن دو عبارت جبری نیز اتحاد جبری میگوییم. مثلاً دو عبارت \(\Large (x+2)^2\) و \(\Large x^2+4x+4\) را در نظر بگیرید. هر گونه که \(\Large x\) را مقدار دهی کنیم، مقدار دو عبارت با هم برابر خواهد شد. تفاوتی نمیکند \(\Large x\) چه عددی باشد. برای اینکه موضوع را مشاهده کنید، مقدار این دو عبارت را به ازای سه عدد مختلف در جدول زیر به دست آوردهایم:
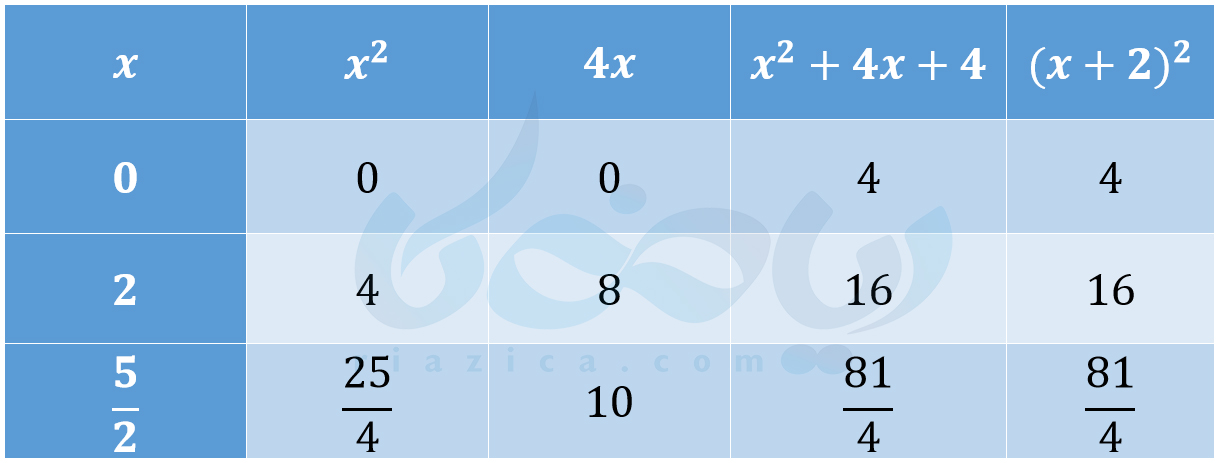
همان طور که میبینید مقدار این دو عبارت جبری به ازای هر سه مقداری که به \(\Large x\) دادیم، با یکدیگر برابر است. البته این اثباتی برای متحد بودن این دو عبارت نیست. زیرا نامتناهی عدد حقیقی وجود دارد و نمیتوانیم همۀ آنها را امتحان کنیم. درستی یک اتحاد جبری به روشهای دیگری صورت میگیرد. در قسمت بعدی از درسنامۀ اتحاد ریاضی نهم هم یک اتحاد مهم را معرفی میکنیم و هم اثبات آن را با یکدیگر میبینیم.
اتحاد مربع دو جمله ای
برای به دست آوردن مربع یک چندجملهای، از اتحاد مربع دو جمله ای استفاده میکنیم که به صورت زیر است:
\(\LARGE (x+y)^2=x^2+2xy+y^2\)
\(\LARGE (x-y)^2=x^2-2xy+y^2\)
هر کدام از خطوط بالا، یک عبارت هستند. اما به دلیل آنکه تنها در یک علامت تفاوت دارند، به هر دوی آنها اتحاد مربع دو جمله ای میگوییم. این اتحاد میگوید مربع مجموع دو جمله برابر است با مربع جملۀ اول به علاوۀ دو برابر حاصل ضرب جملهها به علاوۀ مربع جملۀ دوم. همچنین، مربع تفریق دو جمله برابر است با مربع جملۀ اول منهای دو برابر حاصل ضرب جملهها به علاوۀ مربع جملۀ دوم. اثبات این دو رابطه نیز به سادگی صورت میگیرد. برای اثبات رابطۀ اول داریم:
\(\LARGE (x+y)^2=(x+y)(x+y)\)
\(\LARGE =x^2+xy+yx+y^2\)
\(\LARGE =x^2+2xy+y^2\)
برای اثبات رابطۀ دوم نیز داریم:
\(\LARGE (x-y)^2=(x-y)(x-y)\)
\(\LARGE =x^2-xy-yx+y^2\)
\(\LARGE =x^2-2xy+y^2\)
به مثال بعدی از درسنامۀ اتحاد ریاضی نهم توجه کنید.
مثال از درسنامۀ اتحاد ریاضی نهم
مثال 1: عبارت \(\Large (\sqrt{x}+\frac{2}{3})^2\) را با استفاده از اتحاد مربع دو جمله ای ساده کنید.
حل: مربع جملۀ اول برابر است با \(\Large x\)، دو برابر حاصل ضرب جملهها برابر است با \(\Large 2\times \sqrt{x} \times \frac{2}{3}\)، مربع جملۀ دوم نیز برابر است با \(\Large (\frac{2}{3})^2\). بنابراین عبارت داده شده در مسئله برابر است با:
\(\LARGE x+2\times \sqrt{x} \times \frac{2}{3}+(\frac{2}{3})^2\)
\(\LARGE =x+\frac{4}{3} \sqrt{x} +\frac{4}{9}\)
به مثال بعدی از درسنامۀ اتحاد ریاضی نهم توجه کنید.
مثال 2: حاصل عبارت \(\Large (\frac{1}{2}yz-3x^5)^2\) را با استفاده از اتحاد مربع دو جمله ای به دست آورید.
حل: مربع جملۀ اول برابر است با \(\Large \frac{1}{4}y^2z^2\)، دو برابر حاصل ضرب جملهها برابر است با \(\Large 2\times \frac{1}{2}yz \times 3x^5\)، مربع جملۀ دوم نیز برابر است با \(\Large (3x^5)^2\). بنابراین عبارت داده شده در مسئله برابر است با:
\(\Large \frac{1}{4}y^2z^2-2\times \frac{1}{2}yz \times 3x^5+(3x^5)^2\)
\(\LARGE =\frac{1}{4}y^2z^2-3x^5yz +9x^{10}\)
به قسمت بعدی از درسنامۀ اتحاد ریاضی نهم توجه کنید.
استفاده از اتحاد مربع دو جمله ای در محاسبات
از اتحادها میتوان در ساده سازی برخی از محاسبات نیز استفاده کرد. برای اینکه بهتر متوجه شوید، به مثال زیر دقت کنید.
مثال 3: مقدار \(\Large (5001)^2\) را با استفاده از اتحاد مربع دو جمله ای به دست آورید.
حل: شاید به ظاهر، عبارت داده شده ارتباطی به اتحاد مربع دو جمله ای نداشته باشد؛ زیرا با به دست آوردن حاصل ضرب \(\Large 5001 \times 5001\) پاسخ مشخص میشود. اما اگر بیشتر دقت کنیم، میبینیم که عبارت داده شده را میتوان به صورت زیر نوشت:
\(\LARGE (5001)^2=(5000+1)^2\)
\(\LARGE =5000^2+2 \times 5000 \times1 + 1^2\)
\(\LARGE =25000000+10000 + 1\)
\(\LARGE =25010001\)
همان طور که دیدید، محاسبۀ عبارت داده شده با استفاده از اتحاد مربع دو جمله ای بسیار سادهتر از محاسبۀ عبارت \(\Large 5001 \times 5001\) بود. بنابراین گاهی استفاده از اتحادها، در انجام محاسبات نیز میتواند به ما کمک کند.
اتحاد مزدوج
زمانی که میخواهیم حاصل جمع دو عبارت جبری را در تفریقشان ضرب کنیم، از اتحاد زیر استفاده میکنیم:
\(\LARGE (x+y)(x-y)=x^2-y^2\)
به این اتحاد، اتحاد مزدوج میگوییم. اثبات این اتحاد نیز به سادگی و تنها با ساده کردن عبارت سمت چپ اتحاد صورت میگیرد. یعنی داریم:
\(\LARGE (x+y)(x-y)\)
\(\LARGE =x^2-xy+yx-y^2\)
\(\LARGE =x^2-y^2\)
در ادامۀ درسنامۀ اتحاد ریاضی نهم از اتحاد مزدوج برای ساده کردن عبارات و حل مسائل استفاده میکنیم.
مثال از اتحاد ریاضی نهم
مثال 4: عبارت \(\Large (3a+2)(3a-2)\) را با استفاده از اتحاد مزدوج ساده کنید.
حل: اگر عبارت داده شده را با اتحاد مزدوج مقایسه کنیم، \(\Large 3a\) را میتوانیم همان \(\Large x\) در نظر بگیریم و \(\Large 2\) را همان \(\Large y\) در نظر بگیریم. بر این اساس داریم:
\(\LARGE (3a+2)(3a-2)\)
\(\LARGE =(3a)^2-2^2\)
\(\LARGE =9a^2-4\)
به مثال بعدی از درسنامۀ اتحاد ریاضی نهم توجه کنید.
مثال 5: عبارت \(\Large (3x-4+2y)(3x+4-2y)\) را با استفاده از اتحاد مزدوج ساده کنید.
حل: عبارت داده شده را میتوانیم به صورت زیر بنویسیم:
\(\Large (3x-(4-2y))(3x+(4-2y))\)
حال اگر دقت کنید، میتوانیم از اتحاد مزدوج استفاده کنیم. زیرا عبارت \(\Large 4-2y\) در پرانتز اول جمع و در پرانتز دوم تفریق شده است. بنابراین عبارت بالا برابر است با:
\(\LARGE (3x)^2-(4-2y)^2\)
\(\LARGE =9x^2-(16-16y+4y^2)\)
\(\LARGE =9x^2-16+16y-4y^2\)
همان طور که دیدید، برای محاسبۀ \(\Large (4-2y)^2\) از اتحاد مربع دو جمله ای کردیم. به قسمت بعدی از درسنامۀ اتحاد ریاضی نهم توجه کنید.
استفاده از اتحاد مزدوج در محاسبات
از اتحاد مزدوج نیز مانند اتحاد مربع دو جمله ای میتوان در ساده کردن محاسبات استفاده کرد. به مثال زیر توجه کنید.
مثال 6: مقدار \(\Large 99 \times 101\) را با استفاده از اتحاد مزدوج به دست آورید.
حل: طبیعتاً بدون استفاده از اتحاد مزدوج نیز میتوانیم مقدار خواسته شده را به دست آوریم. اما استفاده از اتحادها کار ما را بسیار آسان خواهد کرد؛ به خصوص زمانی که با اعداد بزرگ سر و کار داشته باشیم. عبارت داده شده در مسئله را به صورت زیر و با استفاده از اتحاد مزدوج محاسبه میکنیم:
\(\LARGE 99 \times 101\)
\(\LARGE =(100-1) \times (100+1)\)
\(\LARGE =100^2-1^2\)
\(\LARGE =10000-1\)
\(\LARGE =9999\)
در قسمت بعدی از درسنامۀ اتحاد ریاضی نهم با یک اتحاد دیگر آشنا خواهیم شد.
اتحاد جمله مشترک
زمانی که دو عبارت جبری در یکدیگر ضرب شده باشند به طوری که یک یا چند جمله بین آن دو مشترک باشد، از اتحاد زیر استفاده میکنیم:
\((x+a)(x+b)=x^2+(a+b)x+ab\)
به این اتحاد، اتحاد مزدوج میگوییم. اثبات این اتحاد نیز به سادگی و تنها با ساده کردن عبارت سمت چپ اتحاد صورت میگیرد. یعنی داریم:
\(\LARGE (x+a)(x+b)\)
\(\LARGE =x^2+xb+ax+ab\)
\(\LARGE =x^2+(a+b)x+ab\)
همان طور که میبینید، ابتدا از خاصیت پخشی استفاده کردیم و سپس \(\Large x\) را فاکتور گرفتیم. در ادامۀ درسنامۀ اتحاد ریاضی نهم از اتحاد جمله مشترک برای ساده کردن عبارات جبری استفاده میکنیم.
مثال از اتحاد ریاضی نهم
مثال 7: عبارت \(\Large (x+2)(x+3)\) را با استفاده از اتحاد جمله مشترک ساده کنید.
حل: جملۀ \(\Large x\) در هر دو عبارت مشترک است. بنابراین میتوانیم از اتحاد جمله مشترک به صورت زیر استفاده کنیم:
\(\LARGE (x+2)(x+3)\)
\(\LARGE =x^2+(2+3)x+2 \times 3\)
\(\LARGE =x^2+5x+6\)
به مثال بعدی از درسنامۀ اتحاد ریاضی نهم توجه کنید.
مثال 8: عبارت \(\Large (2x-3y)(4y+2x)\) را با استفاده از اتحاد جمله مشترک ساده کنید.
حل: جملۀ \(\Large 2x\) در هر دو عبارت مشترک است. بنابراین میتوانیم از اتحاد جمله مشترک به صورت زیر استفاده کنیم:
\(\LARGE (2x-3y)(4y+2x)\)
\( =(2x)^2+(4y-3y) \times 2x + (-3y) \times (4y)\)
\(\LARGE =4x^2+2xy-12y^2\)
به قسمت بعدی از درسنامۀ اتحاد ریاضی نهم توجه کنید.
استفاده از اتحاد جمله مشترک در محاسبات
از اتحاد جمله مشترک نیز میتوان برای ساده سازی محاسبات استفاده کرد. به مثال زیر دقت کنید.
مثال 9: مقدار \(\Large 98 \times 103\) را با استفاده از اتحاد جمله مشترک به دست آورید.
حل: عبارت داده شده را به صورت زیر بازنویسی میکنیم:
\(\LARGE 98 \times 103\)
\(\LARGE =(100-2) \times (100+3)\)
عدد \(\Large 100\) بین دو پرانتز مشترک است. بنابراین عبارت بالا را با استفاده از اتحاد جمله مشترک به صورت زیر ساده میکنیم:
\(\Large 100^2+(3-2) \times 100 + (-2) \times 3\)
\(\LARGE =10000+100-6\)
\(\LARGE =10094\)
استفاده از ترکیب اتحادها
گاهی برای ساده سازی عبارات جبری لازم است که از چند اتحاد استفاده کنیم. یعنی مثلاً ابتدا با استفاده از اتحاد مزدوج، عبارت جبری را ساده کرده و سپس حاصل آن را با استفاده از اتحاد مربع دو جمله ای به دست آوریم. برای اینکه بهتر متوجه شوید، به مثالهای بعدی از درسنامۀ اتحاد ریاضی نهم توجه کنید.
مثال از استفادۀ ترکیبی از اتحادها
مثال 10: عبارت \(\Large (x-2)^2(x+2)^2\) را ساده کنید.
حل: دو راه داریم. راه اول این است که ابتدا مربع هر پرانتز را با استفاده از اتحاد مربع دو جمله ای به دست آورده و سپس دو پرانتز را در یکدیگر ضرب کنیم. راه دوم این است که ابتدا پرانتزها را با استفاده از اتحاد مزدوج در یکدیگر ضرب کرده و سپس مربع آنها را با استفاده از اتحاد مربع دو جمله ای به دست آوریم. راه دوم کوتاه تر است. بنابراین ابتدا حاصل ضرب دو پرانتز را با استفاده از اتحاد مزدوج به صورت زیر به دست میآوریم:
\(\LARGE (x-2)^2(x+2)^2\)
\(\LARGE =((x-2)(x+2))^2\)
\(\LARGE =(x^2-4)^2\)
حال، عبارتی که به دست آوردیم را با استفاده از اتحاد مربع دو جمله ای ساده میکنیم:
\(\LARGE (x^2-4)^2\)
\(\LARGE =(x^2)^2-2 \times x^2 \times (-4)+4^2\)
\(\LARGE =x^4-8 x^2 +16\)
ویدیو از اتحاد ریاضی نهم
در این ویدیو سه اتحاد پایه نهم با مثالهای متعدد برای شما توضیح داده شده است.
زنگ آخر کلاس اتحاد ریاضی نهم.
در درسنامهای که از ریاضی نهم خواندیم، ابتدا اتحاد جبری را تعریف کردیم. سپس به ترتیب با اتحادهای مربع دو جمله ای، مزدوج و جمله مشترک آشنا شدیم. همچنین با حل مثالهای مختلف، کاربرد این اتحادها در ساده سازی عبارات جبری و محاسبات ریاضی را بررسی کردیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با این مبحث دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





بدون تردید ، میتونم بگم ، فوق العاده هستید
با سلام و عرض ادب
ممنون از نظر لطف شما وانرژی که به ما میدهید برای ادامه راه
عالی بود من دهمم به دردم خورد
با سلام و ادب
خدا رو شکر
عالیییییی
با سلام وادب
ممنون از نگاه شما
واقعا هرچی از خدا میخاید ایشالله براتون فراهم بشه
مرسی ک چیزی به دونسته هام اضافه کردین
با سلام وادب
ممنون از دعای خیر شما نور وعشق الهی رو برای شما میطلبم
عالی?❤️
ممنون از کار خوبتون
عالیییی بود ممنونم
با سلام وادب
خدا رو شکر که مفید بوده
خیلیییی خوب بود
متوجه شدم
سپاسگزارم✨
خیلی خوب بود
با سلام دوست عزیز
ممنون از لطف شما
با عرض سلام و احترام
عالی بود ممنونم
با سلام و احترام خدمت شما.مطالب فوق العاده مفیدی بود.ممنون از تلاش شما.
با سلام ممنون از نگاه شما
سلام
خیلی خیلی خوب بود خیلیم ب دردم خورد ممنون
واقعا ممنون
با سلام و سپاس
خدا رو شکر که مورد توجه شما قرار گرفته
یک سوال داشتم. دسته اماری، تعداد دسته ها و میانه و میانگین رو لطفا توضیح بدهید ممنون
با سلام
در پستهای مربوط به خودش توضیح دادیم دوست عزیز
واقعا بکارم اومد
ممنونم
با سلام دوست عزیز
خدا رو شکرمفید بوده برای شما
شما فوق العاده هستید
بدرخشید
سلام دوست عزیز
ممنون از شما ودعای قشنگتون
خب سلام من هشتم و توی مدرسه نمونه درس میخونم به همین دلیل برای نهم میخوان مارو از الان برای آزمون های تیزهوشآن آماده کنن و الان بعضی از مطالب نهم را اعم از همین اتحاد را داریم تا زمان برای تست زنی برای آزمون های لیگ و تیزهوشان داشته باشیم ممنون واقعا کمک بزرگی کردید
خب سلام من هشتمم و توی مدرسه نمونه درس میخونم به همین دلیل برای نهم میخوان مارو از الان برای آزمون های تیزهوشآن آماده کنن و الان بعضی از مطالب نهم را اعم از همین اتحاد را داریم تا زمان برای تست زنی برای آزمون های لیگ و تیزهوشان داشته باشیم ممنون واقعا کمک بزرگی کردید
متشکرم عالی بود مخصوصا نمونه سوالاتون
با سلام وادب ممنون از نظر لطف شما به سایت ما
خیلی بدردم خورد
با سلام خدا رو شکر
بد بود👎👎
سلام مجاش بد بود پیشنهاد شما چیه؟